This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-

Great Circles: Spherical Polyhedra Disclosed by Great Circles of the Icosahedron
The 31 great circles of the icosahedron disclose the following spherical polyhedra: the octahedron; icosahedron; pentagonal dodecahedon; icosidodecahedron; tricontahedron; and VE.… Continue reading → Read more
-

Great Circles: Spherical Polyhedra Disclosed by Great Circles of the VE
The 25 great circles of the vector equilbrium (VE) disclose the following spherical polyhedra: the octahedra; the vector equilibrium (VE); the tetrahedron; the rhombic dodecahedron; and the cube.… Continue reading → Read more
-

Polyhedra With Whole Number Volumes
With the regular tetrahedron as the unit measure of volume, most of the regular polyhedra have whole number or rational volumes. Fuller takes credit for this discovery and considered it one his most significant.… Continue reading → Read more
-
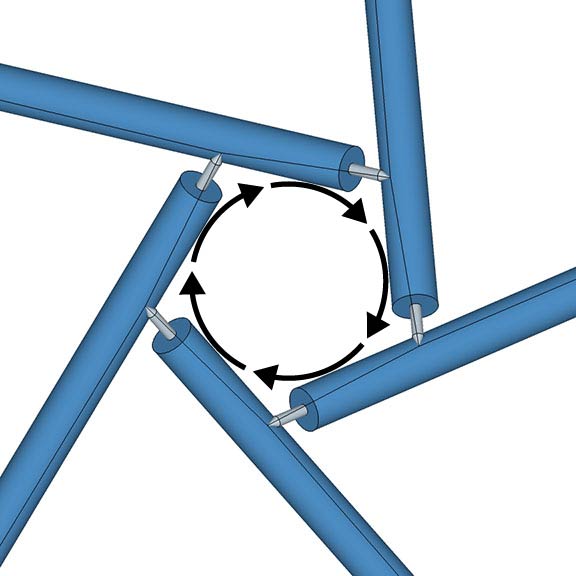
Tensegrity
“Tensegrity” is a portmanteau of tension and integrity. It refers to standalone structures that would have as much integrity in the vacuum of space as on the earth’s surface. In its purest form, a tensegrity structure consists of isolated rigid elements, struts, suspended in an unbroken web of tension, tendons. Fuller’s geodesic domes constitute a… Read more
-
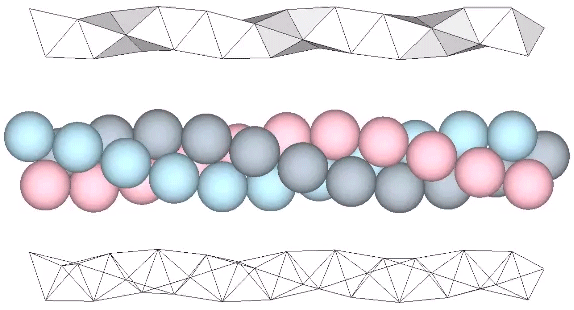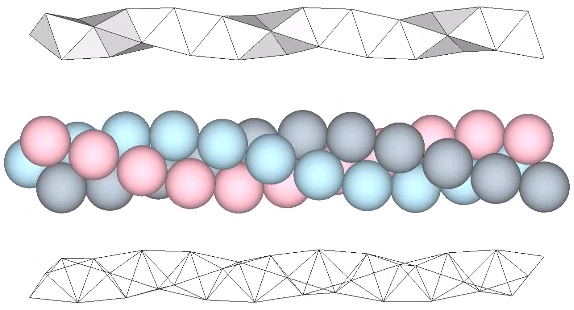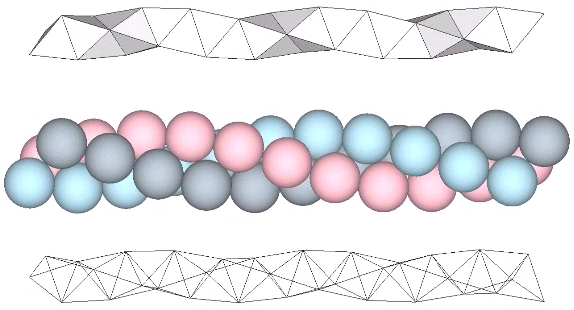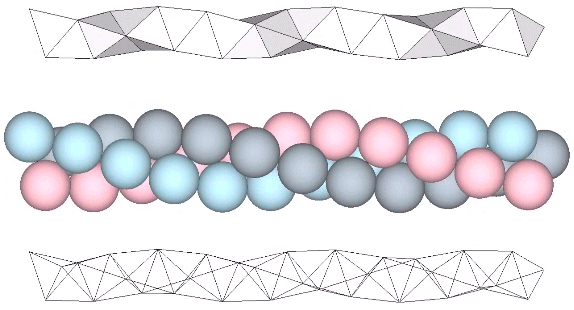
Tetrahelix
Tetrahedra can be face-bonded to form a helical structure Fuller called the “tetrahelix.” It can be constructed as a single, double, or triple helix, oriented either clockwise or counter-clockwise. The single helix completes about ten cycles per 30 tetrahedra; the double helix completes about five, and the triple helix completes about one cycle per 30… Read more
-
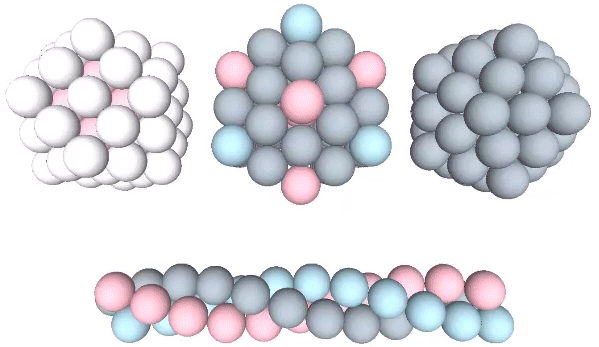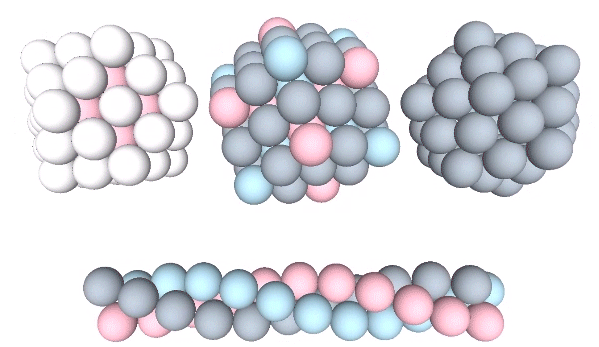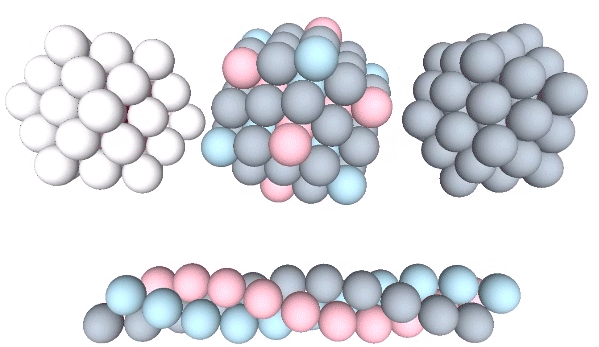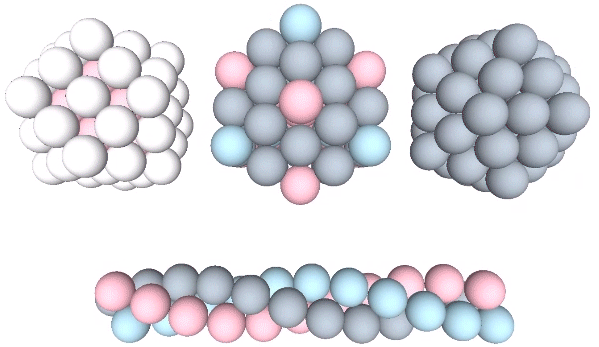
Close-Packing of Spheres
Unit-radius spheres close pack in four fundamentally different ways: 1) radially around a central nucleus to form the isotropic vector matrix; 2) semi-radially to form a semi-isotropic rhomboid matrix; 3) laterally as discrete icosahedron shells, and; 4) and linearly as discrete triple helices of face-bonded tetrahedra.… Continue reading → Read more