This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-
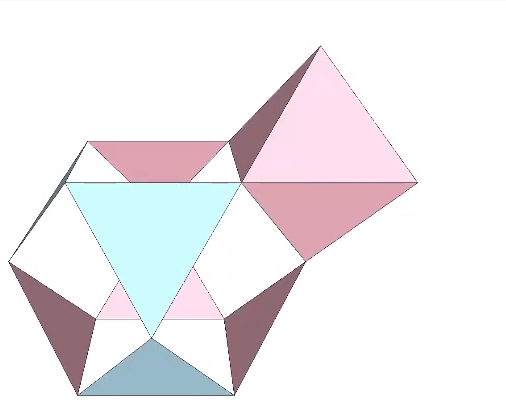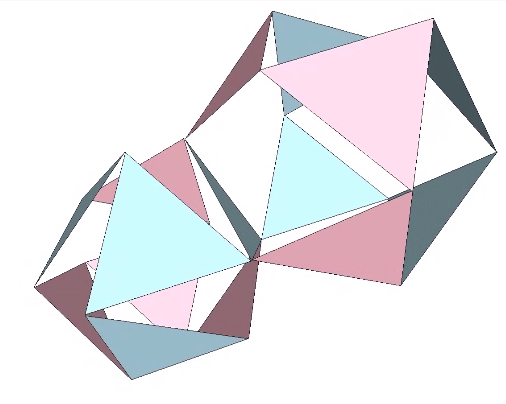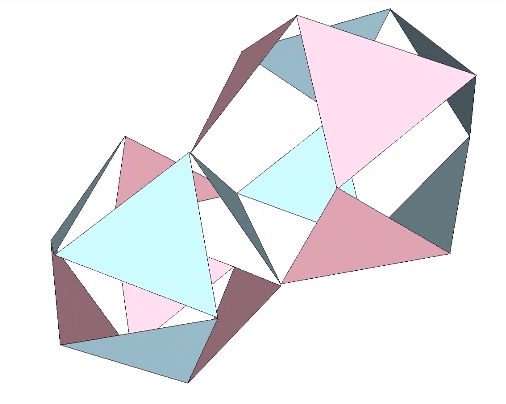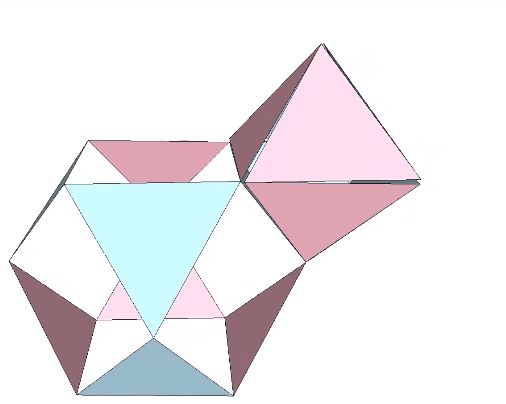
Jitterbug
The Jitterbug is what Fuller called a transformation that occurs when the radial vectors are removed from the otherwise stable configuration of the vector equilibrium (VE). The whole isotropic vector matrix can be made to jitterbug, with VEs transforming into octahedra, and octahedra into VEs. This coordinated transformation of the isotropic vector matrix suggests a… Read more
-
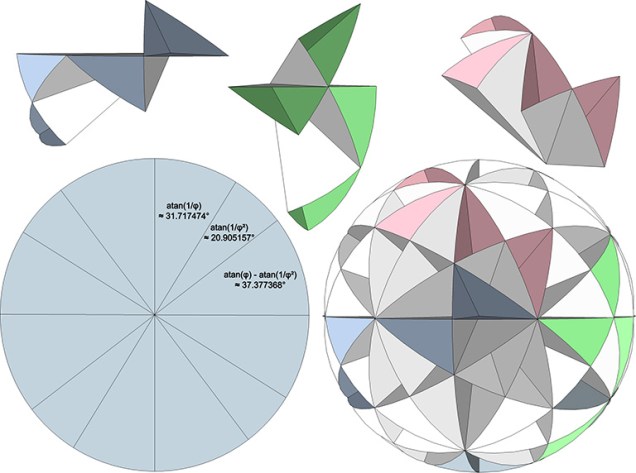
Great Circle Bow-Ties of the Icosahedron
The sets of six, ten, and fifteen great circles of the icosahedron can be modeled by folding circular paper disks into bow-tie-like shapes and fitting them together to form the sphere. … Continue reading → Read more
-
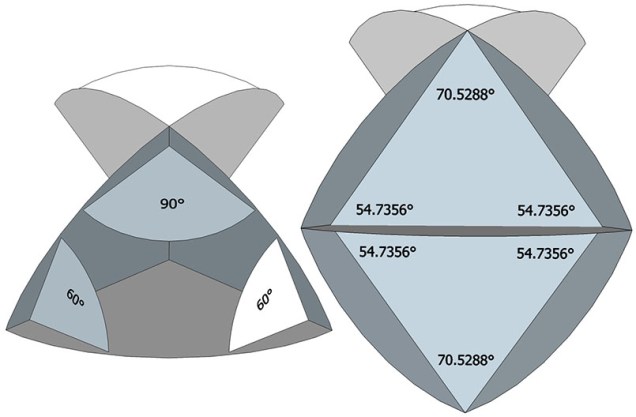
Great Circle Bow-Ties of the VE
If the paper strips unfolded from a polyhedron suggest wave propagation, or the conversion of mass to energy, the alternative construction of folding paper disks into great-circle bow ties perhaps suggests the inverse, the conversion of energy to mass, a beautiful model for the wave-particle duality of energy. In Fuller’s energetic geometry, the great circles… Read more
-
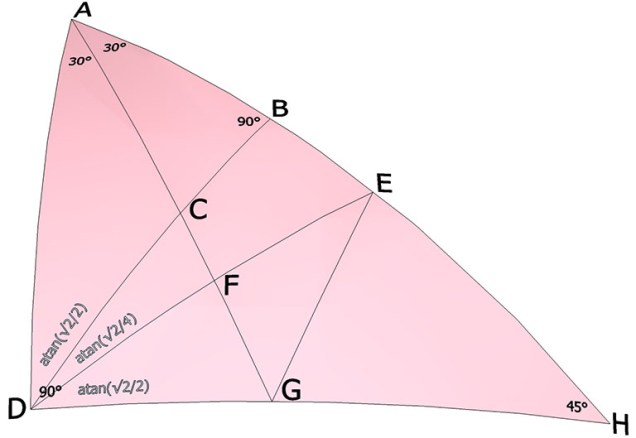
Basic Equilibrium LCD Triangle
The Basic Equilibrium LCD Triangle subdivides the surface of the sphere into 48 equal parts and is derived from the 25 great circles of the vector equilibrium. It is one of three spherical triangles on which all geodesic dome calculations are based. The others are: the basic disequilibrium LCD triangle which subdivides the sphere into… Read more
-
Polyhedra From Polygonal Strips
The tetrahedron, rhombic dodecahedron, octahedron, and icosahedron can all be constructed from the sequential linear folds of a single paper strip. Fuller was interested in the shapes of polyhedron nets, especially those of the quanta modules, but does not seem to have devoted much time (nor has anyone else for that matter) to nets that… Read more
-
T and E Quanta Modules
The T quanta module was part of Fuller’s ongoing effort to find that elusive polyhedron of unit edge length whose tetrahedral volume was evenly divisible by 5. The 30-sided tricontahedron proved promising. It could evenly be subdivided into 120 irregular tetrahedron, each of which would have a volume of 5/120, or 1/24, i.e., the exact… Read more