Explorations

This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.

The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.

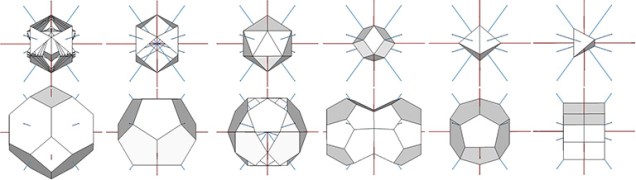
  • Seven Axes of Symmetry

    Seven Axes of Symmetry

    All the regular polyhedra, as well as other polyhedra significant to Fuller’s geometry, align with seven common axes. Fuller has two definitions for his “seven axes of symmetry.” The first definition relates to the great circle sets of the vector equilibrium (VE) and the icosahedron. The 25 great circles of the VE are defined by… Read more

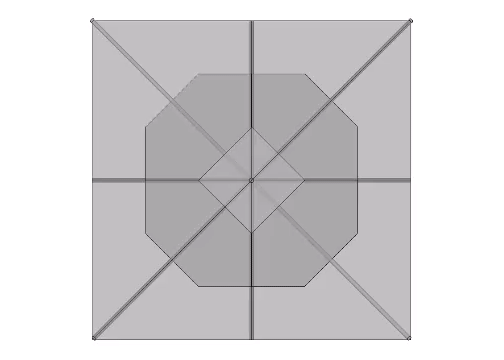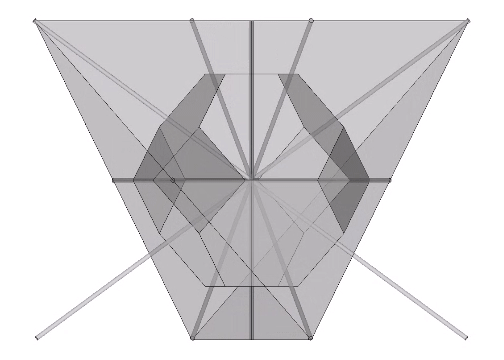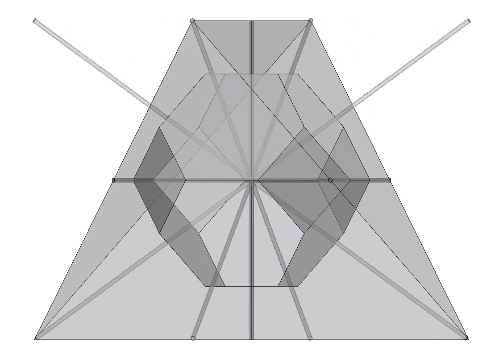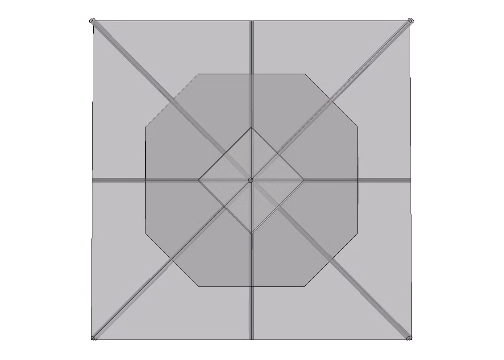
  • Kelvin Truncated Octahedron

    Kelvin Truncated Octahedron

    The Kelvin truncated octahedron, or “Kelvin” is associated with the distribution of nuclei in the isotropic vector matrix, and the structure of foams in the Weaire-Phelan matrix. The Kelvin is a space-filling, fourteen-sided polyhedron with eight hexagonal faces and six square faces, all of equal edge-length. It got its name from a problem posed by… Read more

  • Vector Equilibrium and the “VE”

    Vector Equilibrium and the “VE”

    Vectors connecting the centers of unit-radius spheres clustered around a common nucleus define the vector equilibrium, or “VE”. In the VE, the number of modular subdivisions, i.e. frequency, of the radii is exactly the same as the number of modular subdivisions of the chords. Frequency may refer, then, to the number of shells surrounding the… Read more

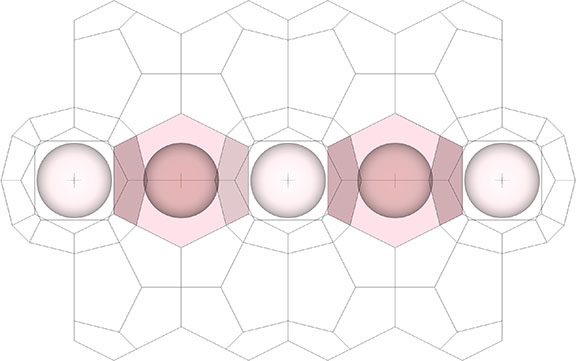
  • Tetrakaidecahedron and Pyritohedron

    Tetrakaidecahedron and Pyritohedron

    There is a curious correlation between the close packing of unit-radius spheres and foams of unit-volume cells. If we partition close-packed spheres into nuclear domains of central spheres surrounded by unique 12-sphere shells, the shells are distributed as Kelvin’s tetrakaidecahedra, but the nuclei themselves are distributed exactly as the pyritohedra are distributed in the Weaire-Phelan… Read more

  • Dual Nature of the Tetrahedron

    Dual Nature of the Tetrahedron

    All polyhedra are either left- or right-handed and, with the exception of the tetrahedron, there is no transformation that can be modeled by which one becomes the other. The handedness of a polyhedron is not readily apparent when viewed as a solid or as a vector model with single-point vertices. However, when modeled structurally as… Read more

  • Icosahedron Inside Octahedron

    Icosahedron Inside Octahedron

    The regular icosahedron can be nested inside the regular octahedron so that eight of its faces are coincident with the eight faces of the enclosing octahedron. The icosahedron’s face is skewed at an angle of 37.76125° (arctan(√(3/5)) from the face of the octahedron and divides its edges into lengths corresponding to golden ratio (Φ). The… Read more