This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-

Twoness: The Multiplicative and Additive Two
At the core of both Fuller’s geometry and his philosophy is the idea that “unity is plural and at minimum two.” You can’t draw a circle without drawing two circles, for example. The circle must be drawn on the surface of some system, and it always divides the system into that which is contained by… Read more
-
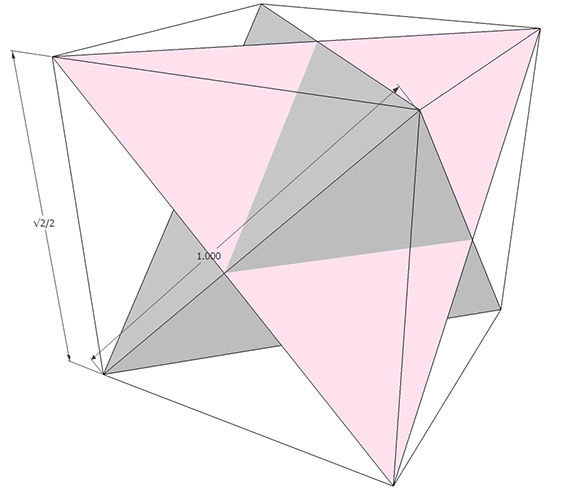
Cube
The cube in Fuller’s geometry is conceived as two tetrahedra, one positive and one negative, sharing a common center of volume. In the absence of the triangulation provided by at least one of the tetrahedra, the cube would lack structure and collapse. The length of the face diagonal, rather than the edge length, is therefore… Read more
-

Icosahedron
The icosahedron is distinguished from the other regular polyhedra in that it has an irrational volume both in tetrahedra and cubes. Its isolation is further reinforced by its axes of spin and the 31 great circles they describe. No great circle unique to the icosahedron passes through any point of contact with spheres radially close-packed… Read more
-

Great Circles: The 31 Great Circles of the Icosahedron
The 31 great circles of the icosahedron are formed from its 10 face-to-face axes, 15 edge-to-edge axes, and 6 vertex-to-vertex axes. None unique to the icosahedron pass through any point of contact with adjacent spheres radially close-packed in the isotropic vector matrix. The 6 great circles pass through no point of contact, including those between… Read more
-

Great Circles: The 25 Great Circles of the Vector Equilibrium (VE)
The 25 great circles of the vector equilibrium are formed from its 12 edge-to-edge axes, 6 vertex-to-vertex axes, 4 triangular-face-to-triangular face axes, and 3 square-face-to-square-face axes. All 25 great circles pass through one or more points of contact between adjacent spheres radially close-packed in the isotropic vector matrix.… Continue reading → Read more
-

Isotropic Vector Matrix
The vector equilibrium (VE) and the isotropic vector matrix constitute the core of Fuller’s geometry. Its discovery is one of Fuller’s earliest memories, from a kindergarten class in his childhood home of Milton, Massachusetts. Given semi-dried peas and toothpicks, and a visual deficit as yet uncorrected by the strong glasses he wore all his life,… Read more