This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-
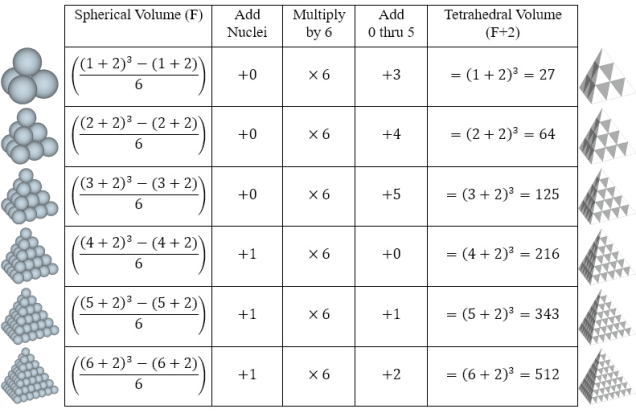
Concentric Sphere Shell Growth Rates
In Section 971 of Synergetics, Fuller documents a 6-part repeating pattern he uncovered in the close packing of spheres in triangular and tetrahedral clusters, which he also relates to the number of unique pairings possible between objects in a set. I’ve provided the short title. The title he proposed is, “Relationships Between First and Third… Read more
-

Golden Ratio
The golden ratio turns up again and again in both Fuller’s and more conventional geometry, and recognizing it when you see it might lead to discoveries otherwise overlooked.… Continue reading → Read more
-

Pi and the Synergetics Constants
The first appearance of Fuller’s synergetics power constants is in a paper he published in 1950 called the Dymaxion Hierarchy of Vector Generated Field-, Volume-, Mass-, Charge-Potential of Geometric Forms. It was Fuller’s first exposition of his “Dynamic Energetic Geometry,” later to be renamed Synergetics. The paper was republished, without modification, as Table 963.10, in… Read more
-

Areas and Volumes in Triangles and Tetrahedra
The article explains how to calculate areas and volumes in equilateral triangles and regular tetrahedra, directly. The only difference between the 90 degree and 60 degree formulas is how we measure height. For areas, the height is measured at 60 degrees from the base. For volumes, the height is measured at arctan(√2) from the base.… Read more
-

Calculating the Tetrahedral Volumes of Regular Polyhedra
When calculating volumes in units of tetrahedra, what would otherwise be perpendicular measurements are instead measured at an angle of atan(√2) from the horizontal. This angle corresponds to the angle the edges of the regular tetrahedron make with their base. Multiplying the perpendicular value, h, by √6/2 gives h’, and h’ is then multiplied by… Read more
-
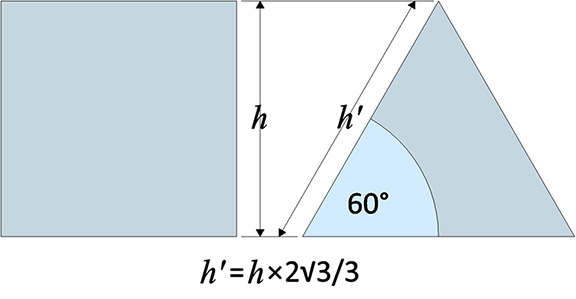
Calculating the Triangular Areas of Regular Polygons
When calculating areas in units of equilateral triangles, what would otherwise be perpendicular measurements are instead measured at an angle of 60 degrees from the horizontal. This angle corresponds to the angle the edges of the triangle make with their base. Multiplying the perpendicular value, h, by 2 times the square root of 3 divided… Read more