This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-

Pyritohedron Dimensions and Whole-Number Volume
The pyritohedron and its space-filling complement, the tetrakaidecahedron, have identical whole-number rational volumes whether measured in units of regular tetrahedron or cubes. For tetrahedral volume, the unit vector is taken to the be the height of the tetrakaidecahedron’s tall pentagonal face. For cubic volume, the unit vector is the base of its pentagonal face.… Continue… Read more
-

Geodesics
The name “geodesic” refers to Fuller’s early conviction that only a triangular latticework of geodesic lines would serve to distribute local stresses evenly throughout the system he patented under the name “Geodesic Dome” in 1954. As the domes evolved into the systems of mostly partial great circles and lesser circles described here, the term “geodesic… Read more
-
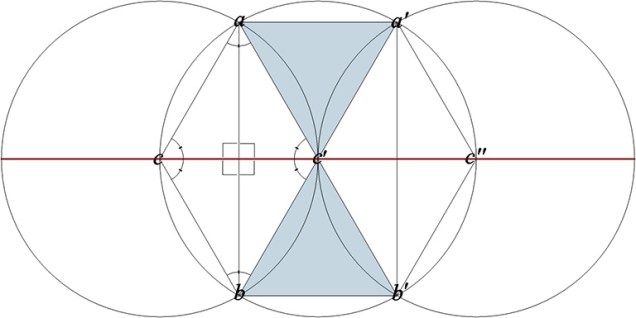
Operational Geometry
All of Fuller’s geometry is “operational” in the sense that it is conveyed and verified by physical models. By way of introducing his operational geometry, Fuller would recall the basic operations of Euclidean geometry. Anyone who’s been through grade school has probably been taught how to use a draftsman’s compass, a straight edge, and a… Read more
-
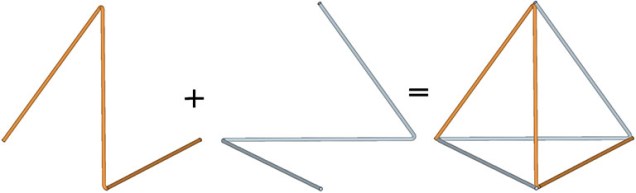
Tetrahedron
Nature’s simplest structural system is the tetrahedron. Regular tetrahedra, however, do not combine to fill all-space (as do cubes, for example). In order to fill all-space, the regular tetrahedron must be complemented by the regular octahedron. Together they produce what Fuller conceived as the simplest, most powerful structural system in the universe, the octahedron-tetrahedron system,… Read more
-

Octahedron
In order to fill all-space, the regular tetrahedron must be complemented by the regular octahedron. Together they produce what Buckminster Fuller conceived as the simplest, most powerful structural system in the universe, the octahedron-tetrahedron system. If we stack octahedra edge-to-edge to create a larger octahedron we discover that we have inadvertently produced eight tetrahedra at… Read more
-
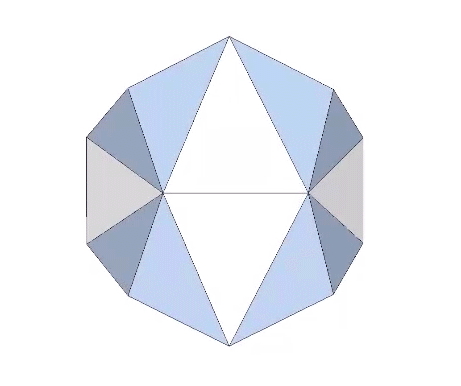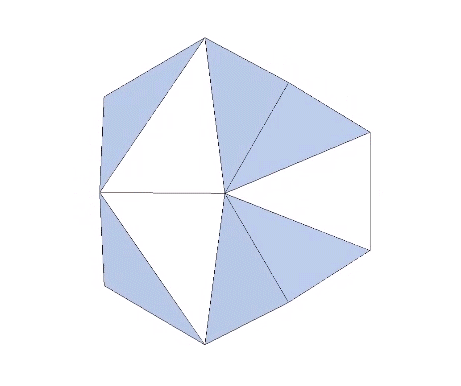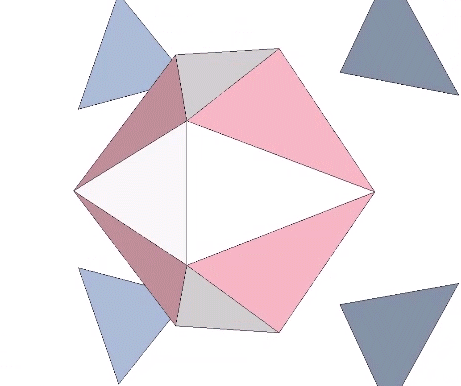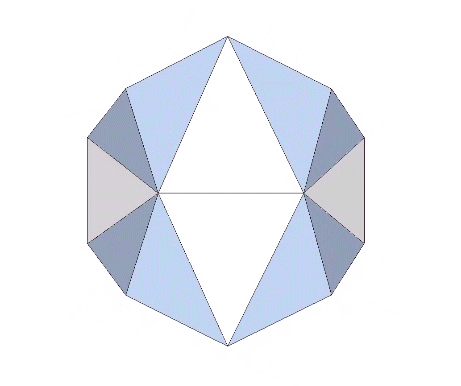
Pentagonal Dodecahedron
The pentagonal (regular) dodecahedron is related to the counterpart of the regular icosahedron that occurs in the jitterbug transformation, but is otherwise incommensurate with the isotropic vector matrix.… Continue reading → Read more