This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-
Space-Filling Polyhedra as Close-Packed Spheres
The space-filling polyhedra in the sphere model of the isotropic vector matrix associate to occupy all of the vertices in the vector model, not the space between them.… Continue reading → Read more
-
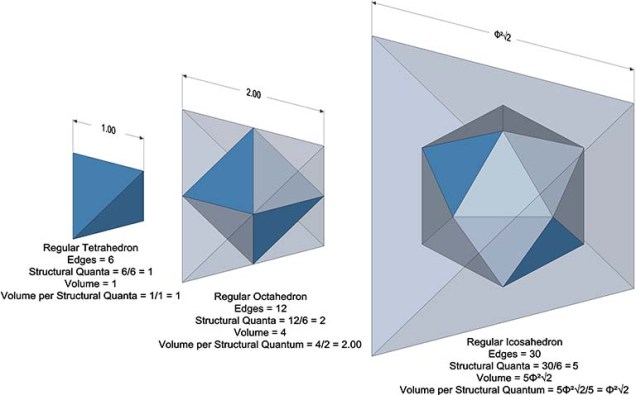
Equivalence of Tetrahedron Edge Length and Structural Quanta per Volume of its Inscribed Polyhedra
A curious mathematical coincidence that I think is worth noting is that the edge length of the tetrahedron in which a unit octahedron or unit icosahedron is inscribed is numerically equivalent to the units of volume, in tetrahedra, provided by Read more
-
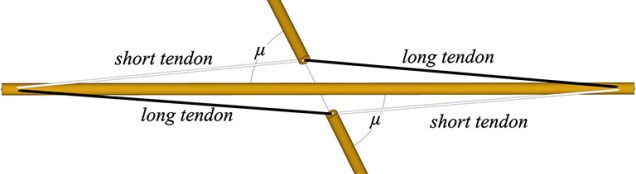
Tensegrity Sphere Equations
The equations described here for determining the strut and tendon lengths of tensegrity spheres improve upon those found in Hugh Kenner’s book, “Geodesic Math and How to Use It” (1976).… Continue reading → Read more
-
The Jessen Orthogonal Icosahedron in the Isotropic Vector Matrix
The Jessen Orthogonal Icosahedron fits neatly between two overlapping vector equilibria (VEs) in the isostropic vector matrix. This is halfway between the nuclear sphere at the center of the VE and the space at the centers of its constituent octahedra. The location is apt, as the Jessen marks the halfway point in the jitterbug transformation… Read more
-
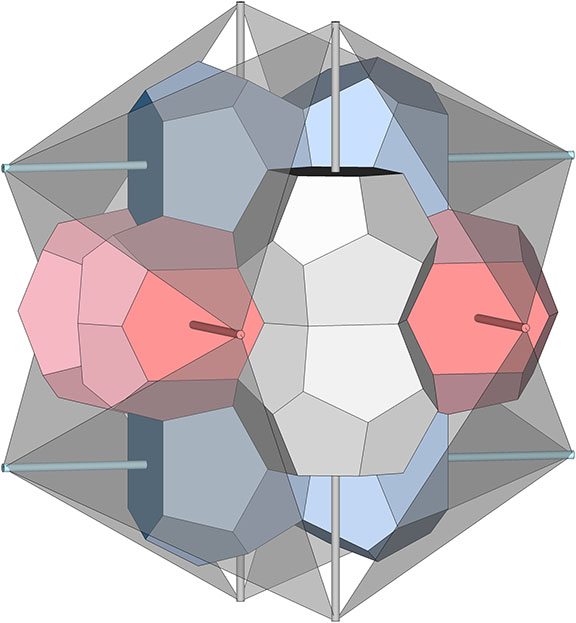
Jessen Orthogonal Icosahedron and Tensor Equilibrium
Precisely midway between its vector-equilibrium phases, the jitterbug describes the shape of the six-strut tensegrity sphere. This is the tensor equilibrium phase of the isotropic vector matrix. Fuller neglected to give the shape a name. Others have taken credit for its “discovery,” and Wikipedia now affirms its identity as the Jessen Orthogonal Icosahedron.… Continue reading… Read more
-
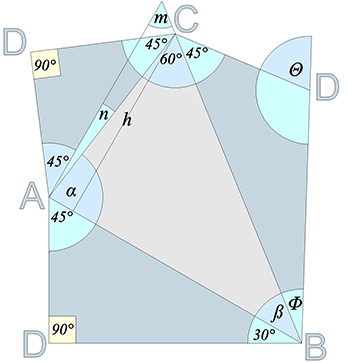
S Quanta Module*
The S quanta module is documented in Synergetics, but it doesn’t seem to have led Fuller anywhere. It was, I think, an attempt to rationalize the volume of the icosahedron, or, at the very least, to calculate the volume of the icosahedron that is inscribed inside the regular octahedron. Fuller’s operational method is provided here,… Read more
The Geometry of Thinking 