This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-
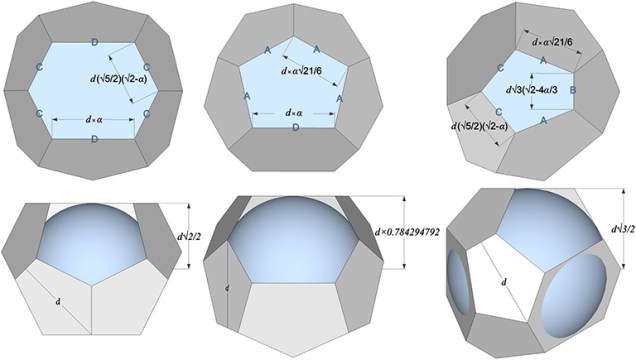
Tetrakaidecahedron Dimensions and Whole Number Volume
To satisfy the Kelvin problem, the volumes of the two polyhedra that constitute the Weaire-Phelan structure, i.e., the pyritohedron and its complementary tetrakaidecahedron, must be identical. By relating this structure to the isotropic vector matrix, we determine the tetrahedral volumes of both to be exactly 24d³, where d is the sphere diameter, and their cubic… Read more
-

Unique Properties of the Tetrahedron
A concise summary of some of the properties that captivated the imagination of R. Buckminster Fuller concerning nature’s simplest system, the tetrahedron. … Continue reading → Read more
-
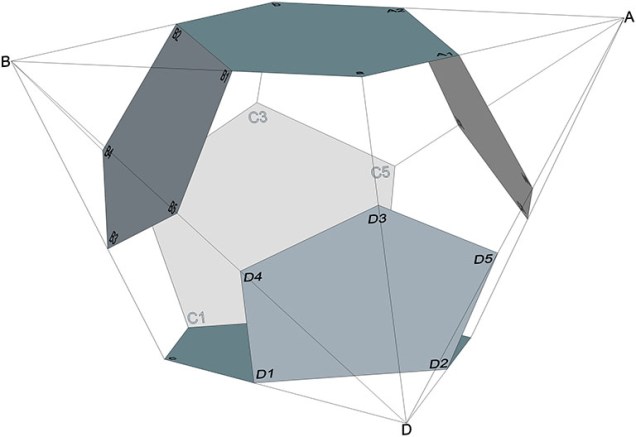
Construction Method for the Pyritohedron and Tetrakaidecahedron of the Weaire-Phelan Structure
This construction produces the rational-volume tetrakaidecahedron and pyritohedron that align with the distribution of nuclei in the radially close-packed spheres of the isotropic vector matrix. See also: Formation and Distribution of Nuclei in Radial Close-Packing of Spheres. Tetrakaidecahedron Begin with a 2√2 by √2 rhombus. Mark the vertices of the long diagonal A and B, and… Read more
-

The 31 Great Circles of the Icosahedron (new illustrations)
This is a supplement to a previous article, Great Circles: The 31 Great Circles of the Icosahedron, with new illustrations I hope will add clarity to the topic. The figure below illustrates the full set of 31 great circles described by rotations about the regular icosahedron’s axes of symmetry. The 31 great circles are divided into… Read more
-

The 25 Great Circles of the VE (new illustrations)
This is a supplement to a previous article, Great Circles: The 25 Great Circles of the Vector Equilibrium (VE), with new illustrations which I think add some clarity to the topic. The figure below illustrates the full set of great circles in the context of the vector equilibrium (VE), both the planar VE (top), and spherical… Read more
-

Spaces and Spheres (Redux)
This is a complete rewrite of a previous article I published on a topic central to Fuller’s geometry. He often said that whenever you draw a circle, you draw two: one convex and the other concave. The same is true of spheres. The universe is finite, and the space surrounding a sphere is just the… Read more