This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-
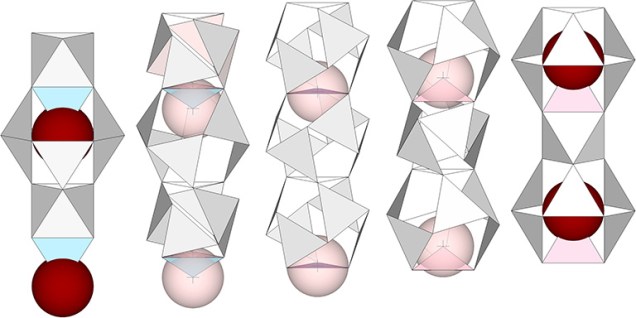
The Polar Pump Model of the Jitterbug
The polar pump model shows how the the jitterbug transformation might be conceived as the shuttling of nuclei along the primary axis of the 4 great circles via the octahedra they straddle. This is the same space-to-sphere, sphere-to-space oscillation as in all other models of the jitterbug, but allows us to visualize the transformation on… Read more
-
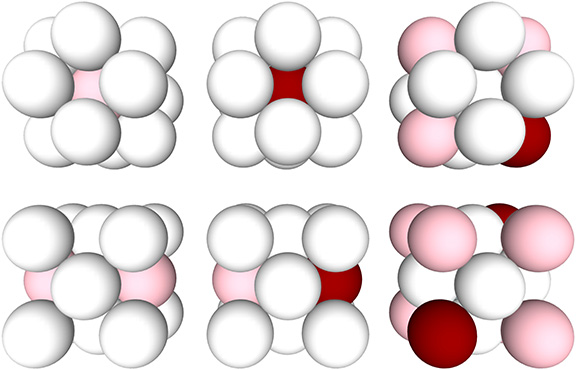
Blinkers, the Jitterbug, and the “Crystalized” Isotropic Vector Matrix
Implicit in the identification of any given sphere in the isotropic vector matrix as a nucleus is the categorization of every other sphere. Identifying a nucleus effectively “crystalizes” the matrix into three unique 13- and 14-sphere clusters of VEs and cubes I’m calling “blinkers.” As the matrix jitterbugs, these clusters generate patterns reminiscent of Conway’s… Read more
-
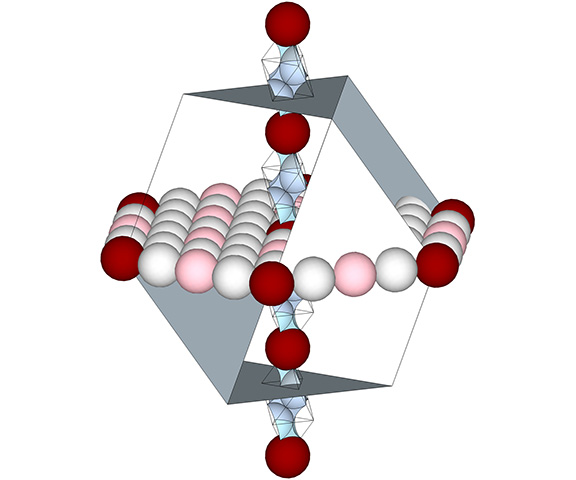
Distribution of Radially Close-Packed Spheres on the 25 Axes and Great Circle Planes of the Vector Equilibrium
The four sets of great circles and the 24 spin axes of the vector equilibrium (VE) are here discussed with regard to the radially close-packed spheres of the isotropic vector matrix.… Continue reading → Read more
-
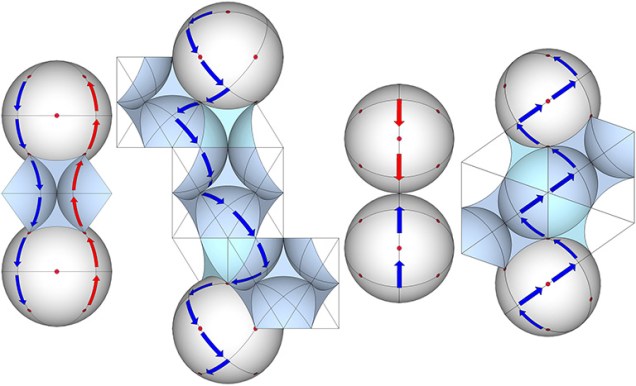
Inter-Sphere Connections via the 25 Great Circles of the VE
The 4 sets of great circles and the 25 spin axes of the vector equilibrium (VE) are here discussed as the shortest-path geodesics between the radially close-packed spheres of the isotropic vector matrix.… Continue reading → Read more
-
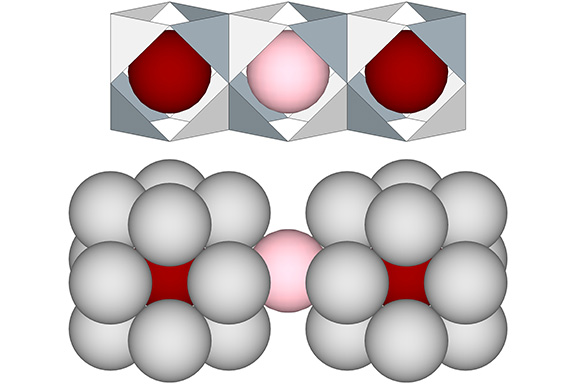
Categories of Spheres in the Isotropic Vector Matrix: Nuclei, F1 Shells, and “Nuclear Voids”
When modeling the distribution of nuclei in the isostropic vector matrix, I distinguish between the nuclei and the 12-sphere shells that isolate and define them. These nuclear domains, each consisting of one nuclear sphere and a 12-sphere shell, defines the vector equilibrium, or VE. Nuclei are distributed throughout the isotropic vector matrix at the centers… Read more
-
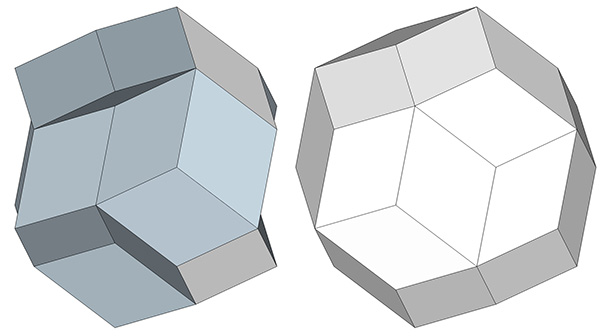
Rhombic Triacontahedron
The rhombic triacontahedron has 30 faces, 60 edges, and 32 vertices. Each of its 30 faces is a golden rhombus, i.e., the length of its long diagonal is related to the length of its short diagonal by φ, the golden ratio: (√5+1)/2 ≈ 1.61803398875 If the long diagonal is taken as d, the length of… Read more