This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-

Anatomy of a Sphere
The point in conventional geometry is replaced by the sphere in Fuller’s geometry. Vertices are the geometric centers of spheres, and vectors connect sphere centers. There are no continuous lines. Surfaces and volumes are point populations, i.e., close-packed spheres or the vertices that define the sphere centers. The minimum point is defined as a vector… Read more
-

A Curious Helical Structure
I stumbled across a curious helical structure that seems to be a cross between a tensegrity prism, a polyhedron, and a tetrahelix. It consists of eight vertex-bonded equilateral triangles that would seem to defy rules for structural rigidity. Its top triangle is rotated six degrees from its bottom triangle, a beautiful whole-number ratio.… Continue reading… Read more
-
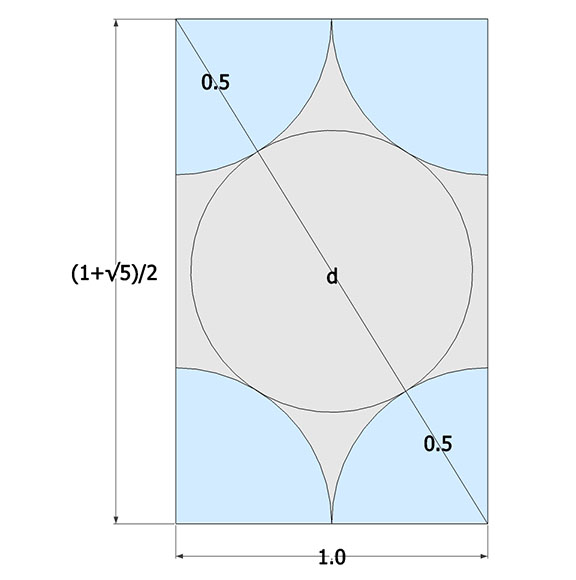
Diagonal of the Icosahedron
If a spherical nucleus were at the center of a close-packed array of spheres in the icosahedron configuration, what would be its radius? That is, by how much must the nucleus shrink when the close-packed array jitterbugs from the VE to the icosahedron? Knowing that the icosahedron can be constructed from the three golden rectangles… Read more
-
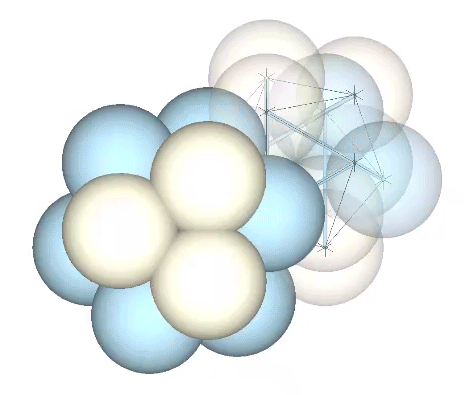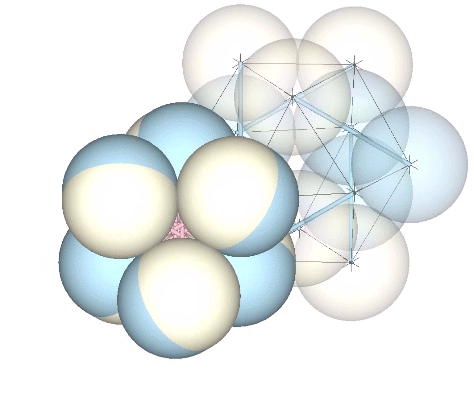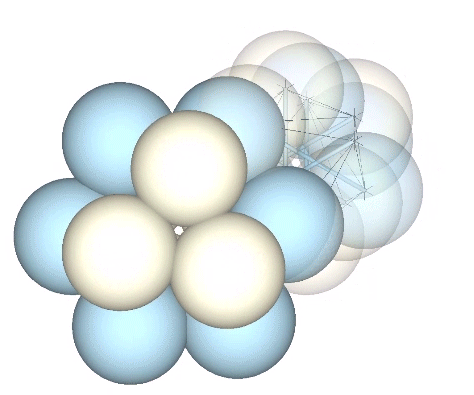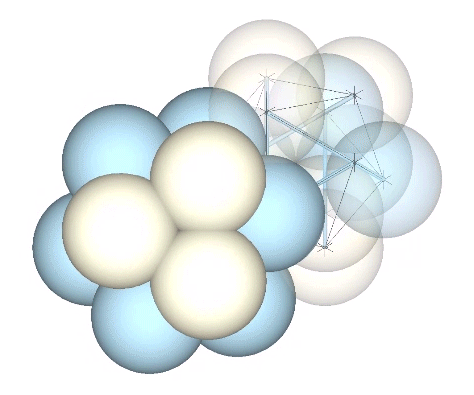
Multiplication and Merger of Spheres in the Jitterbug
We may by now be accustomed to thinking of the fundamental particles that constitute all matter and energy in the universe as clouds of energy, or as waves in a quantum field. So it may not bother us to see these otherwise solid spheres merging and diverging in the spheres model of the jitterbug. However,… Read more
-
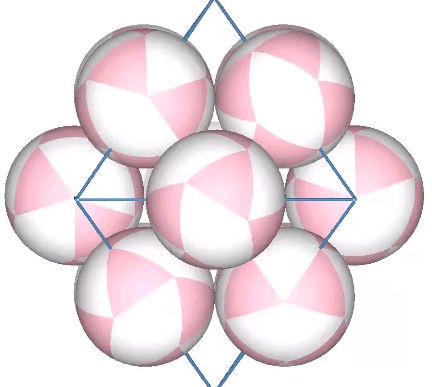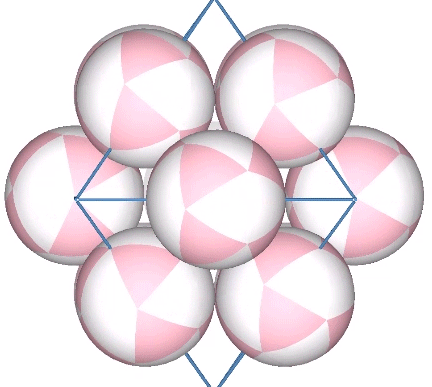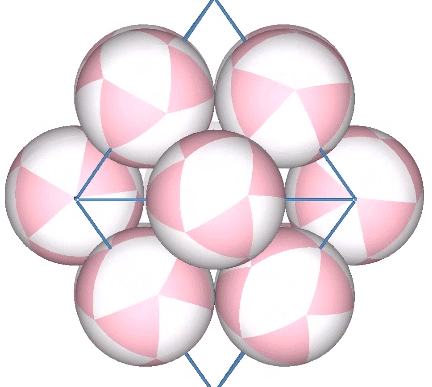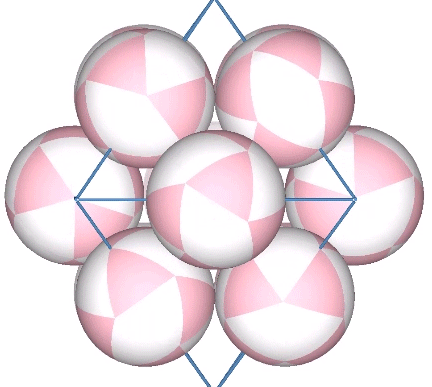
Inter-Geared Mobilities of the De-Nucleated Vector Equilibrium
If we close-pack 12 spheres around a central nucleus and then remove the central sphere, the remaining spheres are free to rotate along twelve axes perpendicular to the radii connecting the sphere centers with their common center. The combined axes describe the regular octahedron. The effect is related to, but not identical with the jitterbug.… Read more
-
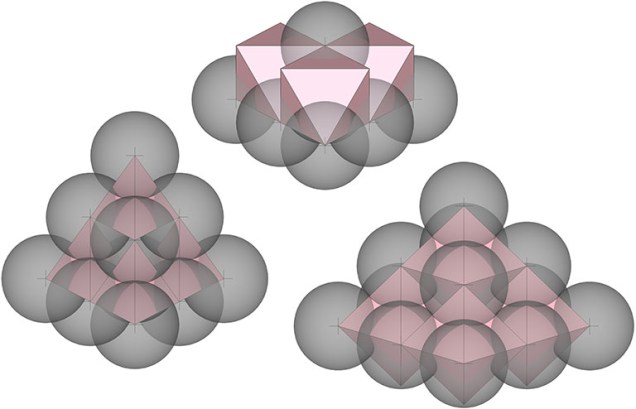
There’s Just One Way to Stack Cannonballs
It may seem that there are at least three ways of stacking cannonballs, i.e., from a triangular base to form a pyramid with three sides; from a square base to form a pyramid with four sides; or as a shallow 3-sided pyramid. But really, there’s only one way. All three arrangements coexist in the radial… Read more