This is an ongoing journal of my personal explorations into the geometry of Richard Buckminster Fuller.
The following articles are arranged chronologically. An alphabetical list may be found in the sidebar. An index to the articles may be found here.
-

Quanta Module Constructions of the Rhombic Dodecahedron
The quanta module construction of the isotropic vector matrix discloses two rhombic dodecahedra, one occupying the positions of the spheres, and the other the space between the spheres. The two constructions can be shown to exchange places during the jitterbug transformation.… Continue reading → Read more
-

Icosahedron Phases of the Jitterbug
Jitterbugging into and out of its ground state, the isotropic vector matrix seems to reach maximum disequilibrium (i.e. maximum expansion) when the contracting vector equilibria (VEs) and expanding octahedra both describe regular icosahedra. It can be shown, however, that the contracting VEs and expanding octahedra cannot pass through their icosahedral phases simultaneously. While one has… Read more
-

Tensegrity Equilibrium and Vector Equilibrium
Another way to visualize the difference between the two equilibrium phases of the jitterbug—tensegrity equilibrium (see Jessen Orthogonal Icosahedron and Tensor Equilibrium, and Tensegrity) and vector equilibrium (see Vector Equilibrium and the “VE”)—is to observe the path followed by the triangles’ vertices. In the case of the tensegrity model of the isotropic vector matrix, and if… Read more
-
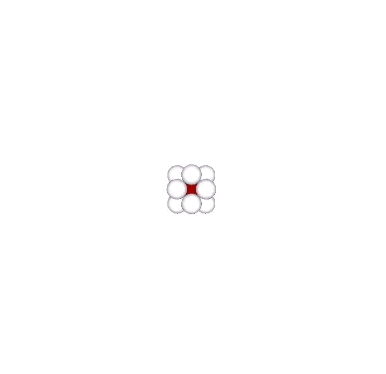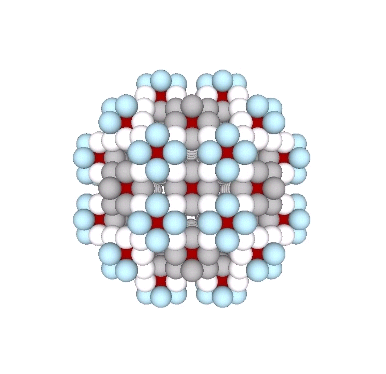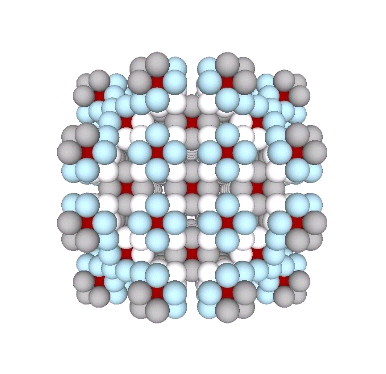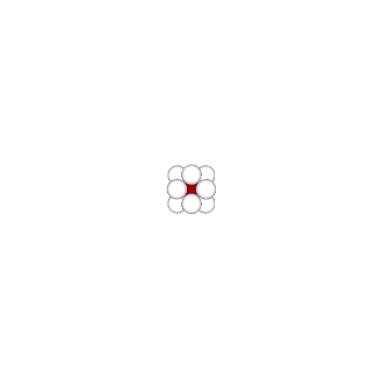
Formation and Distribution of Nuclei in Radial Close-Packing of Spheres
In radial close-packing, every sphere is surrounded by twelve others. Whether or not a given sphere is a nucleus is an arbitrary choice. But the selection of one determines the the regular distribution of all the others. Connecting the centers of unique nuclei forms a grid of rhombic dodecahedra, fourteen around one, not twelve, as… Read more
-
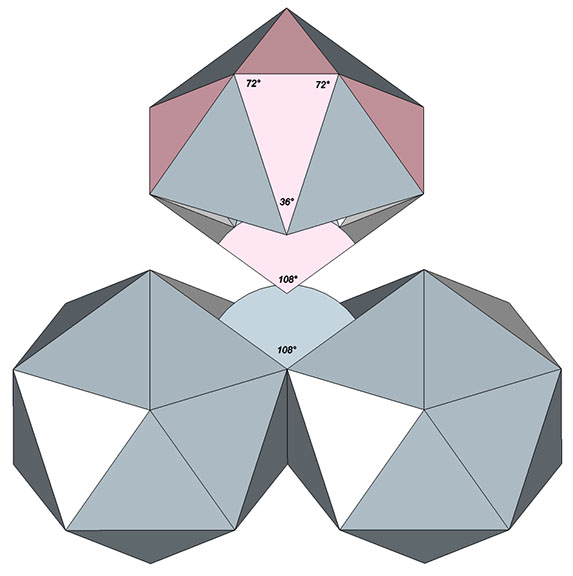
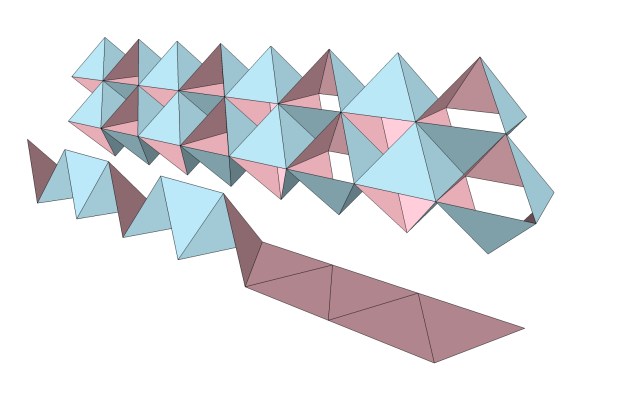
Close Packing of Icosahedra
Regular icosahedra will not close pack to fill all space. They can, however, be edge-bonded to form icosahedral shells and lattices. The study of icosahedron shells may have implications for and resonance with the behavior of cell membranes and other semi-permeable barriers between systems.… Continue reading → Read more
-
Isotropic Vector Matrix as Transverse Waves
A tetrahedron may be constructed from two open-ended triangles. If we use this construction in the isotropic vector matrix, the open ends of each triangle join with similar triangles in the adjacent tetrahedra to form wave patterns that propagate linearly through the matrix, each oriented at 90° to the other. The entire matrix may be… Read more