“Whereas each of the 25 great circles of the vector equilibrium go through the 12 vertexes at least twice; and whereas the 12 vertexes are the only points of inter-tangency of symmetric, unit-radius spheres, one with the other, in closest packing of spheres; and inasmuch as we find that energy charges always follow the convex surfaces of systems; and inasmuch as the great circles represent the most economical, the shortest distance between points on spheres; and inasmuch as we find that energy always takes the most economical route; therefore, it is perfectly clear that energy charges passing through an aggregate of closest-packed spheres, from one to another, could and would employ only the 25 great circles as the great circle railroad tracks between the points of tangency of the spheres, ergo, between points in Universe. We can say, then, that the 25 great circles of the vector equilibrium represent all the possible railroad tracks of shortest energy travel through closest-packed spheres or atoms.”
—R. Buckminster Fuller, Synergetics, 458.01
Fuller proposed that the 25 great circles of the vector equilibrium account for all the routes by which energy is transmitted between spheres in the isotropic vector matrix. Or, to put it more dramatically, the great circles defined by the four sets of 3, 4, 6 and 12 spin axes of the VE represent all possible tracks of shortest energy travel between points in the universe.
See: Great Circles: The 25 Great Circles of the Vector Equilibrium (VE), and; The 25 Great Circles of the VE (new illustrations)
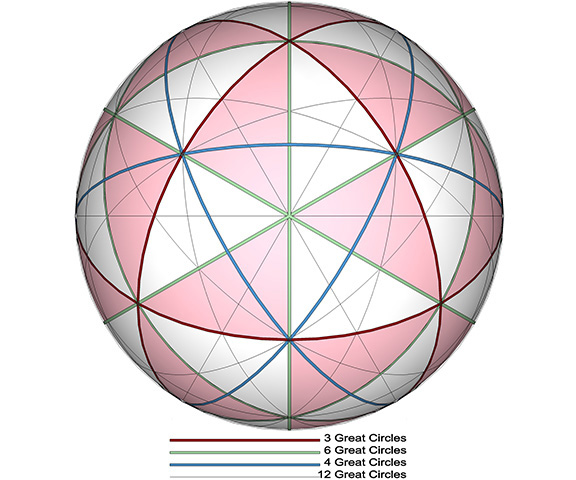
All great circle trajectories may be reduced to combinations of the shortest-distance paths for each set of great circles connecting adjacent spheres on each of the four axes. (See Distribution of Radially Close-Packed Spheres on the 25 Axes and Great Circle Planes of the Vector Equilibrium.)
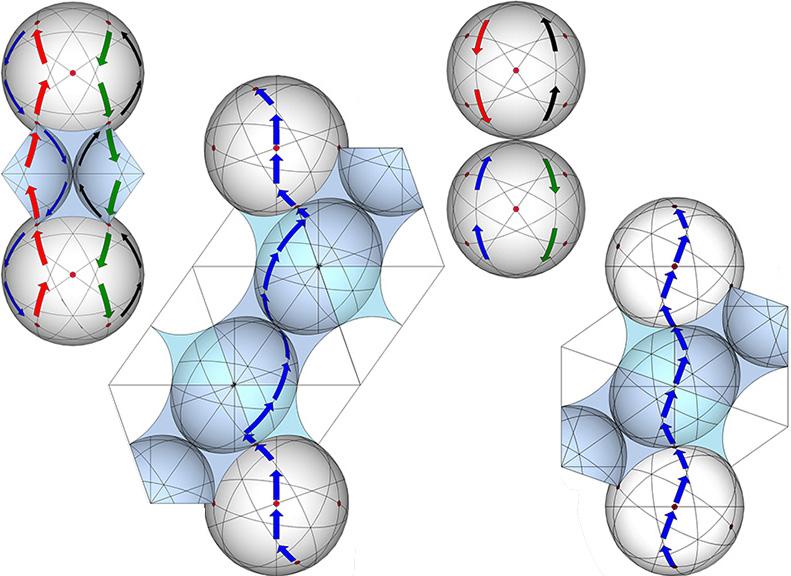
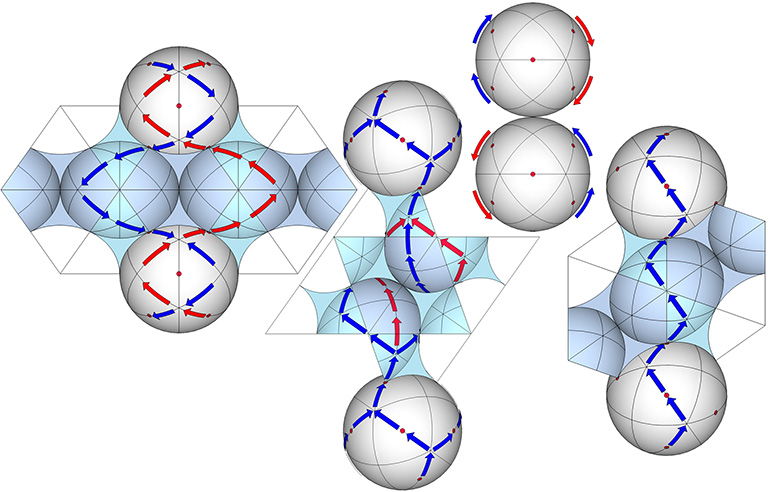
The Set of 3 Great Circles
The great circles in the set of 3 are defined by spin axes running through the centers of opposing square faces of the VE. Each great circle passes through four vertices and therefore has four opportunities with each 360° circuit to connect to an adjacent sphere.
- On the axis of the 3 great circles, the set of 3 reveals four equally efficient paths, two of which are shown below (left).
- On the axis of the 4 great circles, the set of 3 reveals six equally efficient paths, one of which is shown in below (left middle).
- All of the great circle sets connect spheres on the axis of the 6 great circles with equal efficiency, differing only in the number of alternate paths; the set of 3 (right middle), reveals two.
- On the axis of the 12 great circles, the set of 3 reveals two equally efficient paths, one of which is shown below (right).
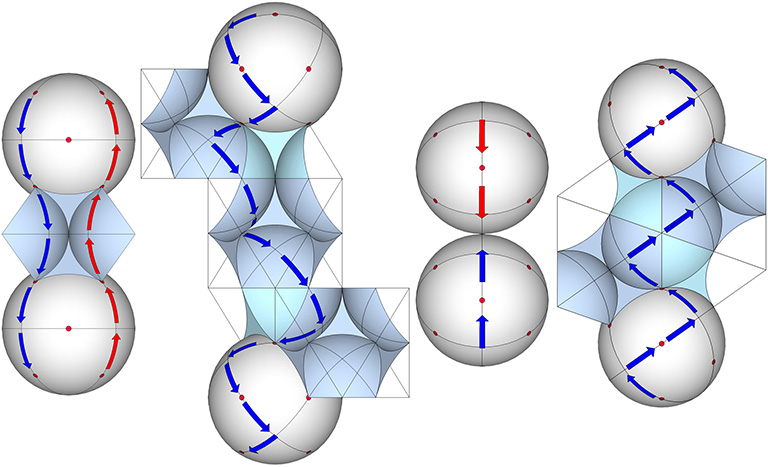
The Set of 4 Great Circles
The great circles in the set of 4 are defined by spin axes running through opposing triangular faces of the vector equilibrium (VE). Each great circle passes through six vertices and therefore has six opportunities with each 360° circuit to connect with an adjacent sphere.
- On the axis of the 3 great circles (top), the set of 4 reveals eight equally-efficient helical routes that complete a cycle every other sphere.
- On the axis of the 4 great circles (middle top), the set of 4 reveals eight equally-efficient helical routes the complete a cycle every fourth sphere.
- On the axis of the 6 great circles (middle bottom), the set of 4 reveals four equally-efficient routes between spheres.
- On the axis of the 12 great circles (bottom), the set of 4 reveals two equally-efficient routes between spheres.
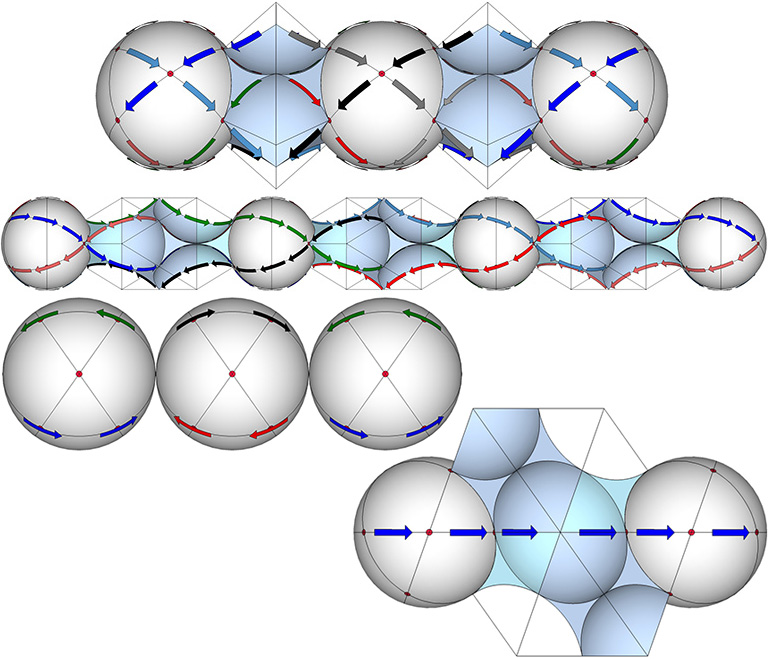
The Set of 6 Great Circles
The great circles in the set of 6 are defined by spin axes running through opposing vertices of the vector equilibrium (VE). Each great circle passes through two diametrically opposed vertices.
- On the axis of the 3 great circles, the set of 6 (left) reveals 4 equally-efficient routes between spheres.
- On the axis of the 4 great circles, the set of of 6 (middle left) reveals a branching network of at least 36 equally-efficient paths.
- On the axis of the set of 6 great circles, the set of 6 (middle right) reveals two equally-efficient paths between spheres.
- On the axis of the 12 great circles, the set of 6 (right) reveals two equally-efficient paths between spheres.
The Set of 12 Great Circles
The great circles in the set of 12 are defined by spin axes running through the midpoints of opposing edges of the vector equilibrium (VE). As with the set of 6, each great circle in the set of 3 passes through two diametrically opposed vertices.
- On the axis of the set of 3 great circles (left), the set of 12 reveals eight equally-efficient routes between spheres.
- On the axis of the 4 great circles (middle left), the set of 12 reveals four equally-efficient paths, one of which is shown.
- On the axis of the set of 6 great circles (middle right), the set of 12 reveals four equally-efficient paths.
- On the axis of the set of 12 great great circles (right), the set of 12 reveals two equally-efficient paths, one of which is shown.