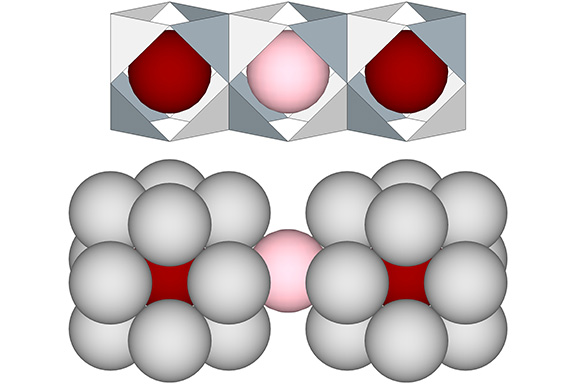
When modeling the distribution of nuclei in the isostropic vector matrix, I distinguish between the nuclei and the 12-sphere shells that isolate and define them. These nuclear domains, each consisting of one nuclear sphere and a 12-sphere shell, defines the vector equilibrium, or VE.
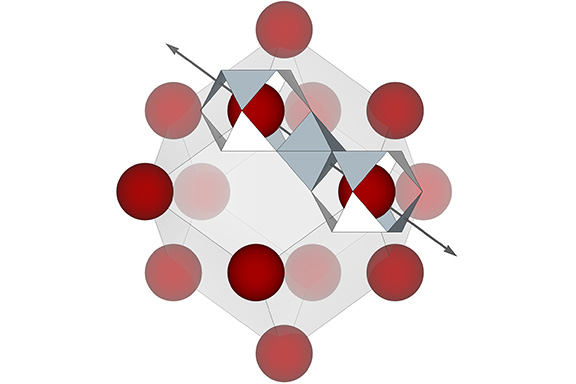
Nuclei are distributed throughout the isotropic vector matrix at the centers and vertices of close-packed rhombic dodecahedra whose edges align with the primary axes of of the vector equilibrium’s 4 great circles. See: Formation and Distribution of Nuclei in Radial Close-Packing of Spheres; and Great Circles: The 25 Great Circles of the Vector Equilibrium (VE); The 25 Great Circles of the VE (new illustrations); and Distribution of Radially Close-Packed Spheres on the 25 Axes and Great Circle Planes of the Vector Equilibrium.
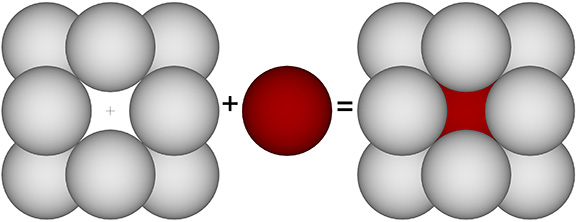
Nuclei and their shells do not close-pack to fill all-space. Between these nuclear clusters are gaps which combine form holes that run laterally through the isotropic vector matrix.
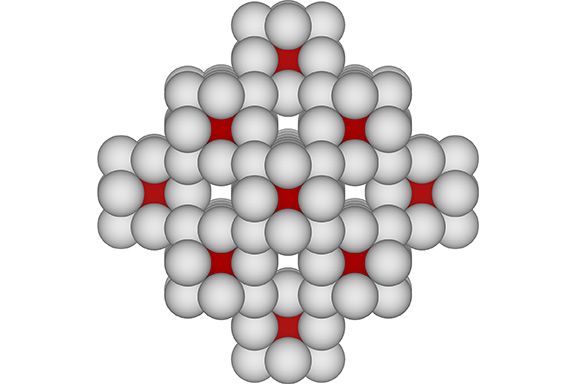
The spheres that fill these voids can be isolated to show that they all lie on a cubic grid which follows the square-face diagonals of close-packed F2 VEs.
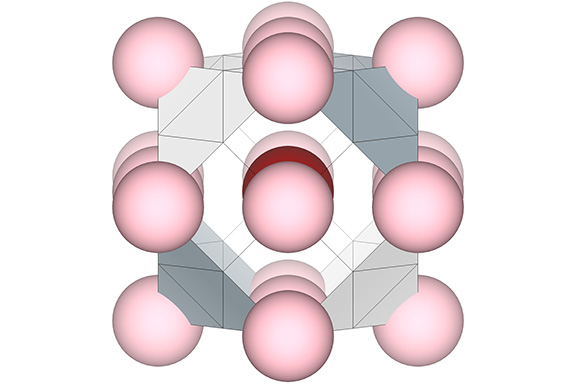
I refer to these as “nuclear voids” because, like the nuclei, each occupies the center of a VE, but unlike the nuclei, they do not have their own 12-sphere shells. Rather, every sphere in direct contact with a “nuclear void” is uniquely identified with the shell of one of its neighboring nuclei.