The Geometry of Thinking

The tetrakaidecahedron of the Weaire-Phelan structure complements the pyritohedron to fill all-space. Together, they constitute what is presently determined to be the best solution to the Kelvin Problem: How can space be partitioned into cells of equal volume with the least area of surface between them?

In previous articles, I demonstrated that the pyritohedra of the Weaire-Phelan structure align perfectly with the distribution of unique nuclei in the radial close-packing of spheres of the isotropic vector matrix. See: Formation and Distribution of Nuclei in Radial Close-Packing of Spheres; Tetrakaidecahedron and Pyritohedron; and Kelvin Truncated Octahedron. I was able to relate the two matrices and rationalize their volumes with reference to the variable, d, the diameter of the unit spheres of the isotropic vector matrix, and the constant α = ³√(√2/2), the length of the pyritohedron’s long edge when d is taken as unity. See: Pyritohedron Dimensions and Whole-Number Volume.

To summarize my conclusions:

• If the sphere diameter, d, is taken as unity, the tetrahedral volumes of both the pyritohedron and the tetrakaidecahedron of the Weaire-Phelan structure work out to be precisely 24d³.

• If its longest edge, a, is taken as unity, then d = 1/α, and the cubic volumes of both the pyritohedron and the tetrakaidecahedron of the Weaire-Phelan structure work out to be precisely 4a³.

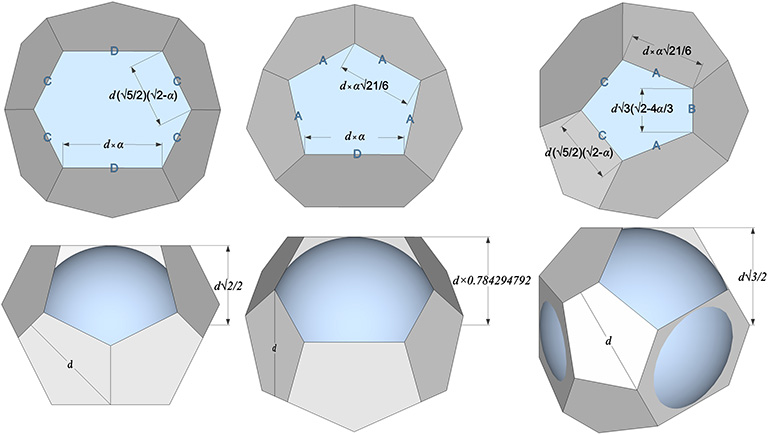
To satisfy the Kelvin problem, the volumes of the two shapes, i.e., the pyritohedron and its complementary tetrakaidecahedron, must be identical. This tetrakaidecahedron has three unique faces: two hexagonal faces; four large pentagonal faces; and eight smaller pentagonal faces, for a total of 14 faces — tetra (four), kai (+), deca (ten), hedron (face). To determine its volume, we’ll need the areas and in-sphere radii for each of its faces.

• in-sphere radius to hexagonal face: d × √2/2
• in-sphere radius to larger pentagonal face: d × ≈ 0.784294792 *
• in-sphere radius to smaller pentagonal face: d × √3/2

* Though it should be possible to work out its precise value algebraically, I have so far been unsuccessful in resolving the in-sphere radius for the larger of the two pentagonal faces into whole number radicals and ratios.

In addition to the in-sphere radii as shown above, we must calculate the surface area for each of the faces. This is most easily accomplished by dividing each face into right triangles.

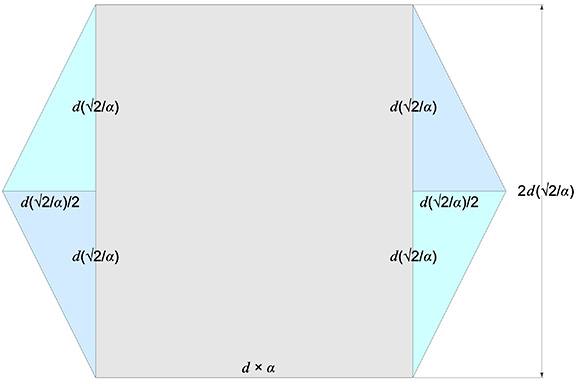
The hexagonal face is divided into four right triangles and one rectangle as follows:

• Four right triangles of atan(1/2), with legs measuring d(√2/α) and d(√2/α)/2.
• One rectangle measuring 2d(√2/α) by (d × α).

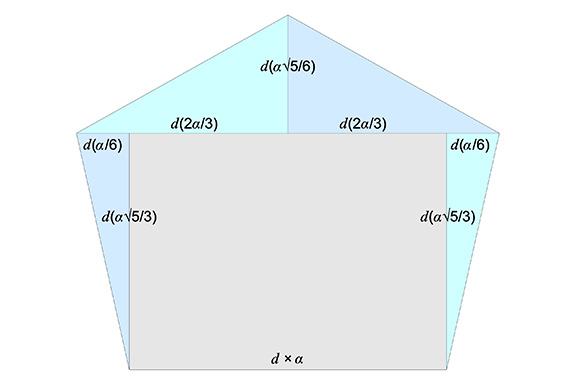
The larger of the two pentagonal faces is divided into four right triangles and one rectangle as follows:

• Two right triangles of atan(√5/4) with legs measuring d(α√5/6) and d(2α/3).
• Two right triangles of atan(√5/10) with legs measuring d(α/6) and d(α√5/3).
• One rectangle measuring d(α√5/3) by (d × α).

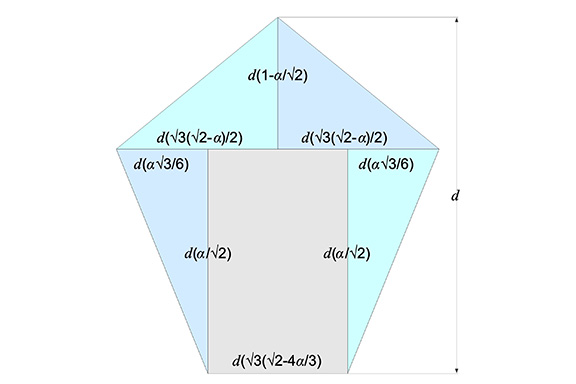
The smaller of the two pentagonal faces is divided into four right triangles and one rectangle as follows:

• Two right triangles of atan(√6/3) with legs measuring d(α√5/6) and d(2α/3).
• Two right triangles of atan(√6/6) with legs measuring d(α/√2) and d(α√3/6).
• One rectangle measuring d√3(√2-4α/3) by d(α/√2).

If d is taken as unity (d = 1), then a = d × α = ³√(√2/2), and

• The hexagonal face has a square area of ≈ 1.20629947402.
• The cubic volume of its polyhedral cone is area/3 × √2/2 ≈ 0.28432751274
• Multiplying by 2 (for the two hexagonal faces) ≈ 0.56865502548
• Converting from cubic to tetrahedral units, multiply the above volume by 6√2 ≈ 4.825197896
• Applying the same calculations to the large pentagonal faces, gives a total tetrahedral volume of 7.874010518.
• And, applied to the small pentagonal faces, gives a total tetrahedral volume of 11.30079158.
• 4.825197896 + 7.874010518 + 11.30079158 = 24, and it therefore follows that its tetrahedral volume is 24d³.

If the long edge (the base of the larger pentagonal face) is taken as unity, the d in our equations = 1/α, then a = α/α = 1. The cubic volumes then are, respectively, 0.804199649, 1.312335086, and 1.883465264, and

• 0.804199649 + 1.312335086 + 1.883465264 = 4, and it therefore follows that its cubic volume is 4a³.