Unique Properties of the Tetrahedron

Greg Frederick

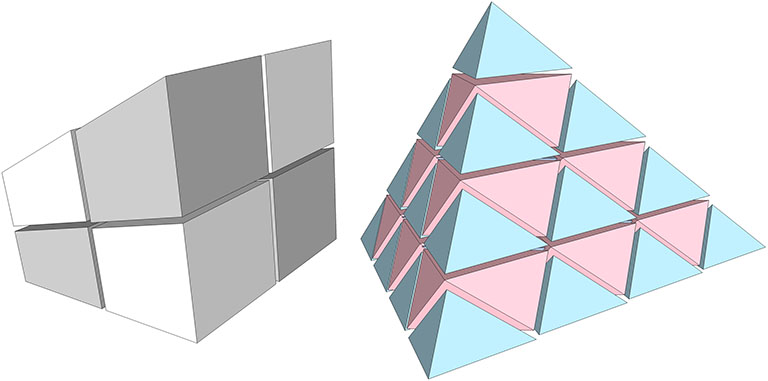
While irregular cubes subdivide into dissimilar six-sided polyhedra, any tetrahedron, regular or irregular, will always subdivide into similar tetrahedra and octahedra.

An irregular tetrahedron (right) subdivided into equal-volume tetrahedron (blue) and octahedra (pink), beside an irregular cube (left) subdivided into dissimilar six-sided polyhedra.
All tetrahedra, regular or irregular, subdivide into similar, equal-volume, tetrahedra and octahedron. This seems to be a property unique to the tetrahedron. An irregular cube, for example, subdivides into dissimilar parts.

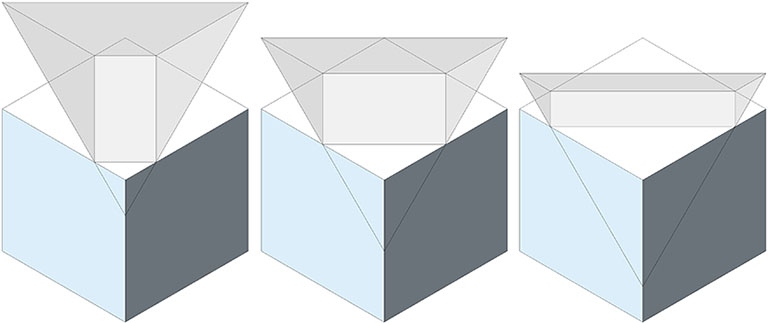
The perimeter of any rectangle defined by the section plane of a regular tetrahedron cutting perpendicularly through its edge-to-edge axis is a constant equal to 2 times its edge length.

Three section planes of a regular tetrahedron oriented on its edge-to-edge axis cut from the top face of cube oriented so that tetrahedron's edges will align with its face diagonals.
As the tetrahedron is pulled out from the cube, the circumference around the tetrahedron remains equal when taken at the points where cube and tetrahedron edges cross.

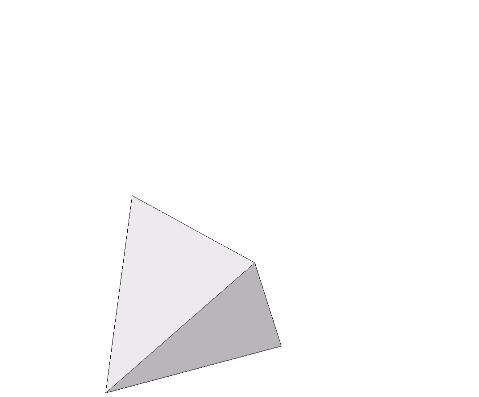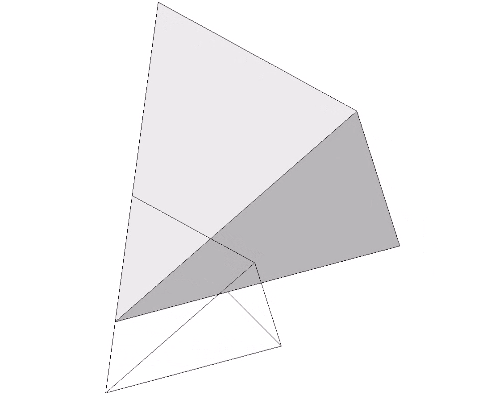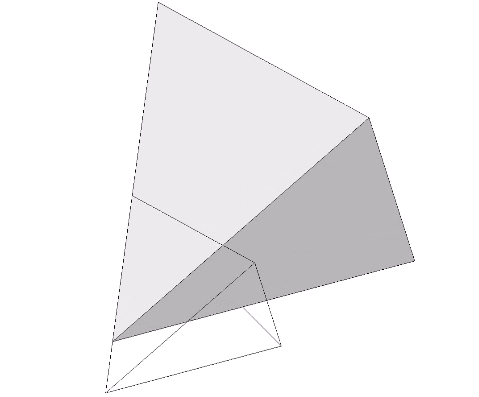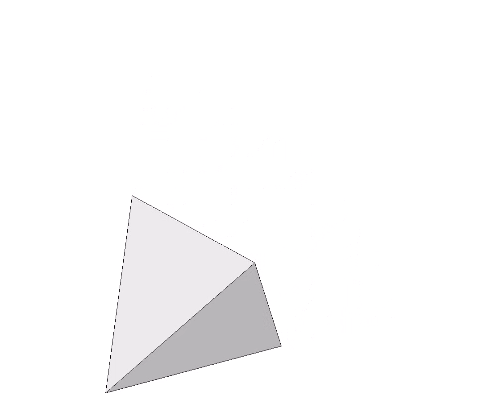
Any tetrahedron, regular or irregular, may be sliced parallel to any one or more of its faces without losing its basic symmetry. Or, as Fuller observed, “only the tetrahedron’s four-dimensional coordination can accommodate asymmetric aberrations without in any way disrupting the symmetrical integrity of the system.” (Synergetics, 100.304)

Four regular tetrahedra, sliced parallel to one each of its four faces.
Any tetrahedron, regular or irregular, may be sliced parallel to any face without losing its basic symmetry.

The pulling outward or pushing inward of one or more faces of the tetrahedron accomplishes the same transformation as uniform scaling would achieve. This accommodation of asymmetrical aberrations while preserving its symmetrical integrity allows for the linear translation of the its center of gravity without actually moving the tetrahedron.

One face of regular tetrahedron is pulled outward to the right, creating a regular tetrahedron of twice its original edge length, then pushed inward from its front face back to its original size, repositioned at new coordinates.
Pushing inward or pulling outward any face of the tetrahedron is identical with uniform scaling. But because it also changes its center of gravity, sequential pushing and pulling on different faces can effectively move the original tetrahedron to new coordinates.

The illustration below shows the same transformation, but with the two actions performed simultaneously, i.e., the pulling outward of one face occurs at the same time and at the same rate as the other face is pushed inward. This is essentially equivalent to a linear translation of the tetrahedron. We can accomplish any translation to any coordinates using this method, something that is possible with no other polyhedron.

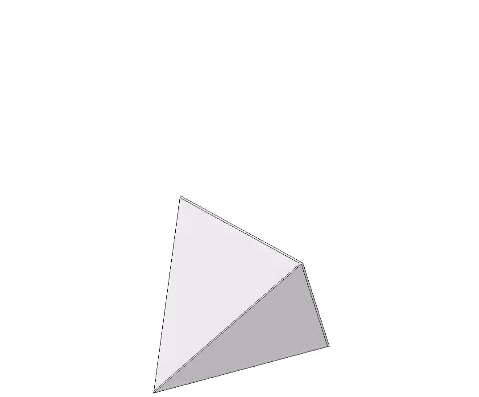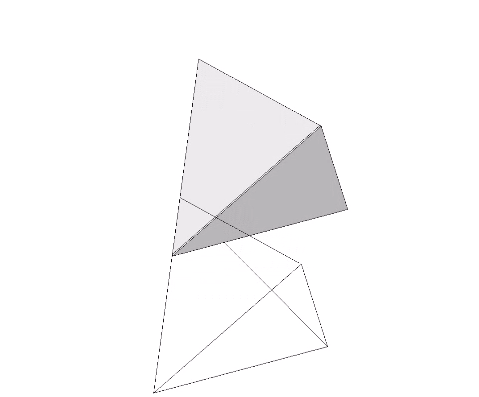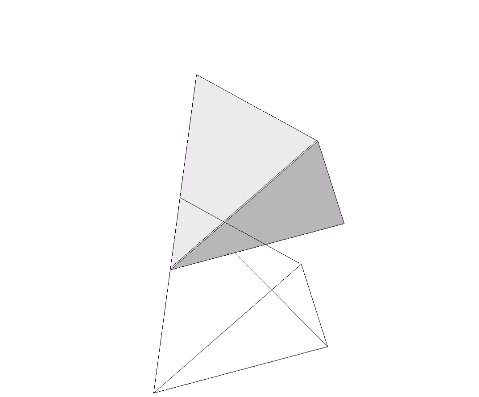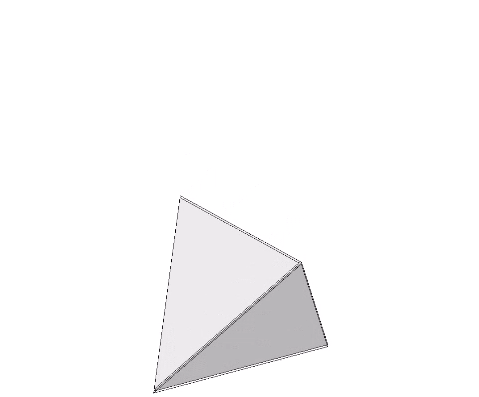
A regular tetrahedron, with one face pulled outward while another face pushed inward at the simultaneously and at the same rate, moves to a new location without any change in shape, scale, or orientation.
The same transformation as above, but with the pushing and pulling happening simultaneously rather than sequentially, produces a transformation identical with positional translation without actually moving the tetrahedron.

The tetrahedron may be turned inside out by pushing a vertex through the opening of its opposite face.

Time lapse sequence of a regular tetrahedron being turned inside out by forcing one of its vertices through the opening of its opposing face.
The tetrahedron is unique among the regular polyhedron in that it may be turned inside out by forcing any one of its vertices through the opening of its opposite face.

Each consecutive (non-oscillating) inside-outing produces a unique orientation of the tetrahedron, and results in an infinite or near-infinite number of helices or helical translations. See also: Tetrahelix.

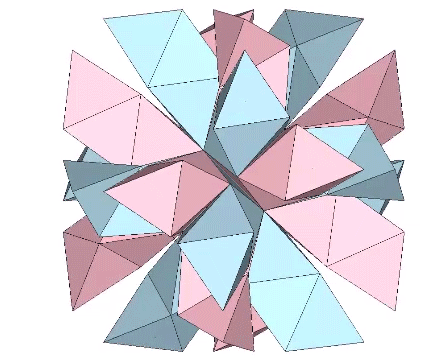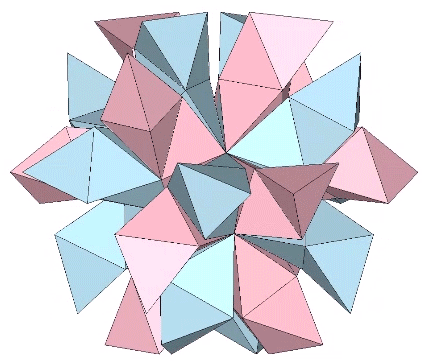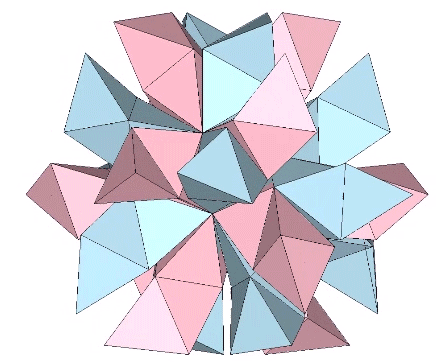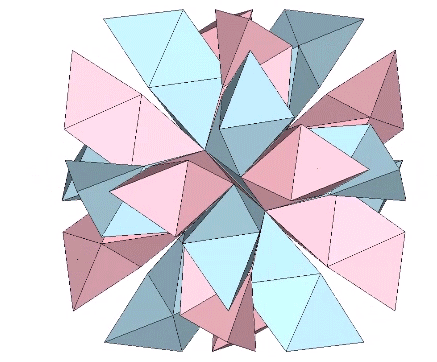
Twelve tetrahelices, six clockwise and six counter-clockwise, emerging from a single tetrahedron.
Sequential inside-outing from a single tetrahedron at the center of this array produces an infinite or near infinite number of unique orientations of the tetrahedron.

The tetrahedron may also turn itself inside-out by rotating three of its triangular faces outward from their common vertex like the petals of a flower. The process may be halted before the vertices rejoin on the opposite side, with the result being an octahedron rather than another tetrahedron. In the octet truss network, the octahedra occupy the spaces between tetrahedra. In the isostropic vector matrix, the octahedron defines the space between the spheres which in turn are defined by positive and negative tetrahedra sharing a common vertex at the center of the vector equilibrium (VE). It seems appropriate, therefore, to conceive of the octahedron as a positive and a negative tetrahedron turned inside-out, as the illustration below demonstrates.

Two regular tetrahedron face-bonded to opposite faces of a regular octahedron. Their three remaining faces open like the petals of a flower to settle into positions occupied by the remaining six faces of the octahedron.
A tetrahedron may be turned inside out by opening three of its faces like the petals of a flower. Two tetrahedra may be turned inside out to constitute the faces of the octahedron.

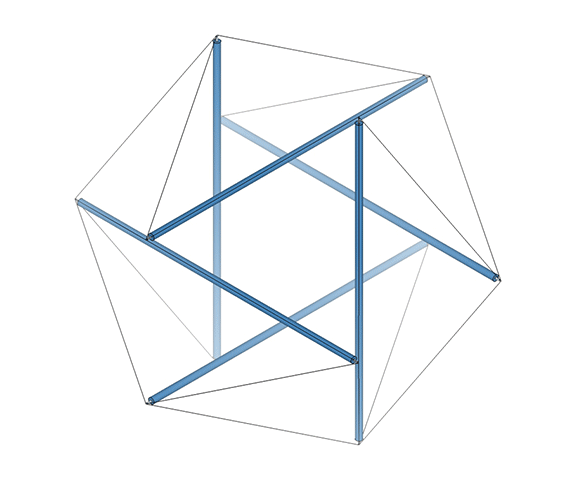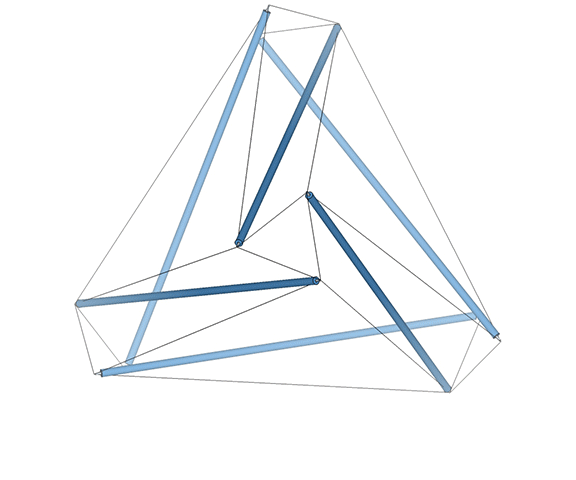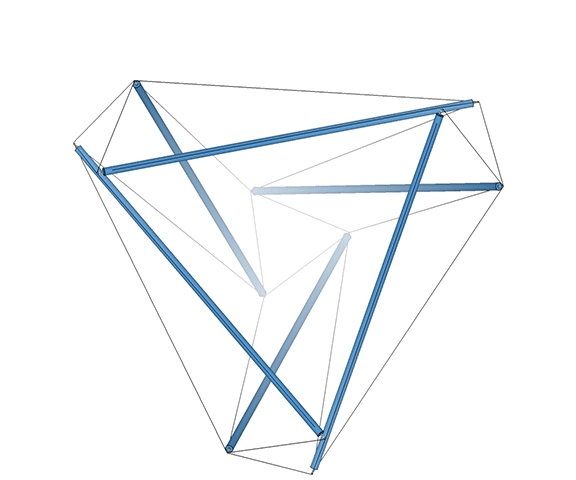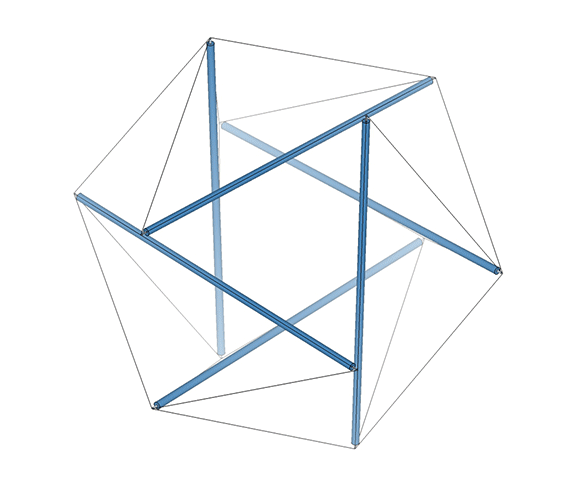
The tetrahedron is uniquely ambidextrous. By this, I mean that we can model the transformation from the positive to the negative tetrahedron non-destructively, i.e., without violating any of the principles that determine its structural or symmetrical integrity. To demonstrate, we need the tensegrity model.

As I’ve said elsewhere, anything in the universe (both physical and metaphysical as Fuller would insist on saying) that may be called structural is structured on tensegrity principles. The structural polyhedra (the tetrahedron, octahedron, icosahedron, and the geodesic polyhedra derived from them) can all be modeled as both polyhedral and spherical tensegrities. But only the tetrahedron may pass through its spherical phase and reverse polarity, with its vertices defined by either a clockwise or counter-clockwise tension loop. The remaining polyhedra are locked into a clockwise or counter-clockwise orientation, and cannot, non-destructively, reverse themselves. See also: Dual Nature of the Tetrahedron.

Two vertices of the tensegrity tetrahedron, one oriented clockwise and the other oriented counter-clockwise.
The vertices of all tensegrity polyhedra are structured in either a clockwise or a counter-clockwise orientation.

The transformation from a positive, or clockwise tetrahedron, to a negative, or counter-clockwise tetrahedron, is what spontaneously drives the jitterbugging of the isotropic vector matrix. See Jitterbug.

The six strut tensegrity sphere transforming into, alternately, a clockwise (positive) tetrahedron, and counter-clockwise (negative) tetrahedron.
The tensegrity tetrahedron is unique among the the structural (tensegrity) polyhedra in that it may spontaneously transform between a clockwise and counter-clockwise orientation

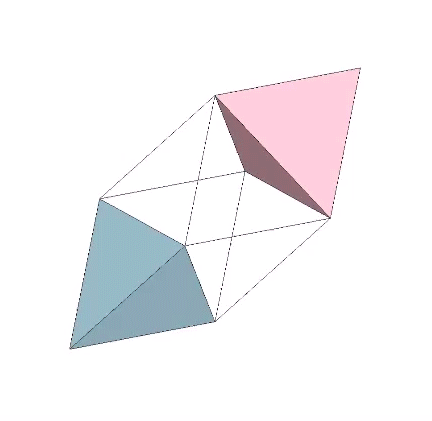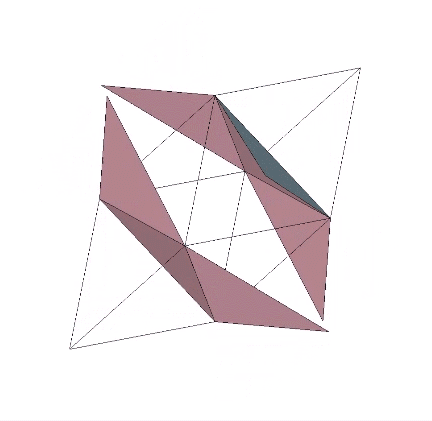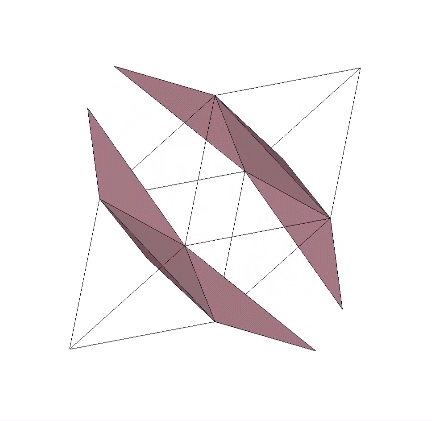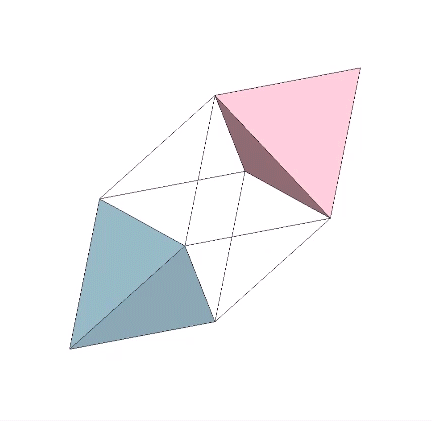
Fuller, taking his A and B quanta modules as inspiration, elaborated on their constancy of volume by continuing the progression out to infinity. Ultimately, we have something indistinguishable from a line, but with the volume of of the original tetrahedron. Fuller regarded this as a model of the photon. While we may imagine a photon traveling through space and time from its origin to its destination, the photon, from its own point of view, is already there.

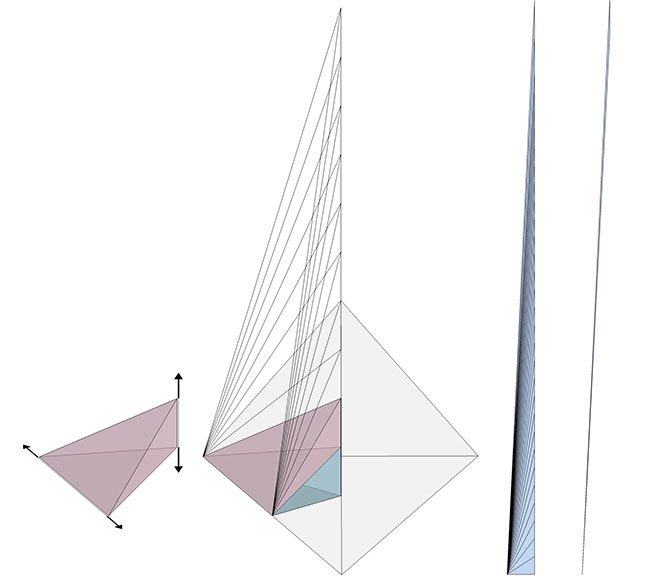
Illustration of the constant volume of tetrahedra sharing equal base areas and identical altitudes
The A (blue) and B (pink) quanta modules have equal volumes by virtue of equal base areas and identical altitudes. It follows that a line, originating at the center of the triangular base of a regular tetrahedron, projected through the apex of the tetrahedron and subdivided into equal increments, will produce additional modules with the same volume as the original A or B Module. As the incremental line approaches infinity the modules will tend to become lines (for right), but lines still having the same volume as the original A or B modules.

A similar constancy is observed when we orient the tetrahedron on its edge-to-edge axes. The highly skewed half-octahedra in the illustration below each have the same volume as the original tetrahedron.

A regular tetrahedron oriented vertically on its edge-to-edge axis, and two highly skewed half octahedron stacked vertically from one if its faces, and with vertically-oriented rectangular bases, their horizontal sides equal to the tetrahedron's edge length, and their vertical sides equal to the tetrahedron's edge-to-edge height.
Half-octahedra produced by pulling one of edges vertically away from its opposing edge, along with one of its faces, in increments equal to its mid-sphere (edge-to-edge) diameter will have the same volume as the original tetrahedron.

Leave a comment