Construction Method for the Pyritohedron and Tetrakaidecahedron of the Weaire-Phelan Structure

Greg Frederick

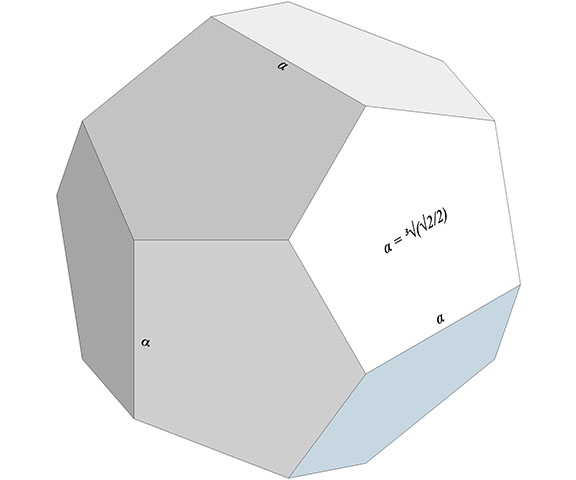
This construction produces the rational-volume tetrakaidecahedron and pyritohedron that align with the distribution of nuclei in the radially close-packed spheres of the isotropic vector matrix. See also: Formation and Distribution of Nuclei in Radial Close-Packing of Spheres.

Tetrakaidecahedron

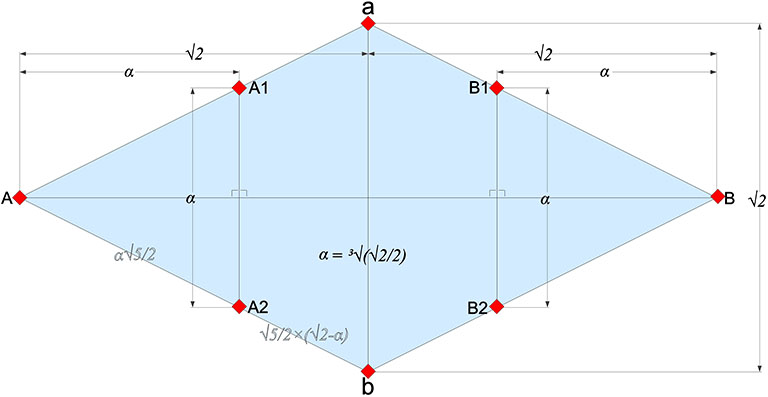
Begin with a 2√2 by √2 rhombus. Mark the vertices of the long diagonal A and B, and the vertices of the short diagonal a and b. On AB, mark points ³√(√2/2), about 0.8908987, in from each end. Lines perpendicular to AB and passing through these points bisect the edges of the rhombus at A1, A2, B1, and B2. (See illustration.)

A rhombus measuring √2 by 2 from which one hexagonal face of the Weaire-Phelan tetrakaidecahedron will be constructed.
The first step in this construction of the Weaire-Phelan tetrakaidecahedon is a 1×2 rhombus dimensioned and scribed as indicated. The points A1, a, B1, B2, b, and A2 define one of its two hexagonal faces.

Replicate the rhombus, rotate 90°, and separate (along the center face normal vector) by √2. Mark points as above, substituting C c for A a, and D d for B b.

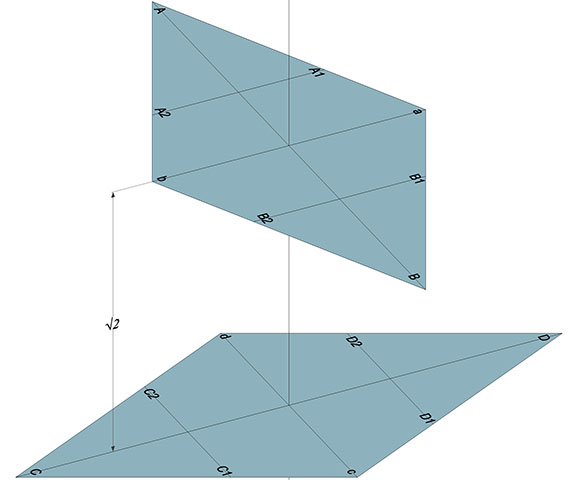
Two √2 by 2√2 rhombuses spaced √2 on their face normal vector from with the two hexagonal faces of the Weaire-Phelan tetrakaidecahedron will be constructed.
A second rhombus spaced one unit (√2) from the first and rotated 90° defines the vertices of the 2nd hexagonal face of the tetrakaidecahedron: C2, d, D2, D1, c, and D2.

Connect the vertices to and create faces: BCcB; BDcB; bCBb; aDBa; ACdA; ADdA; aDAa, and; bCAa. Measure the distance, r, from A to either A1 or A2, and, using this length as the radius, scribe arcs from A on each of its adjacent faces. Repeat for B, C, and D.

The precise value of r is ³√(√2/2)×√5/2, or about 0.996055.

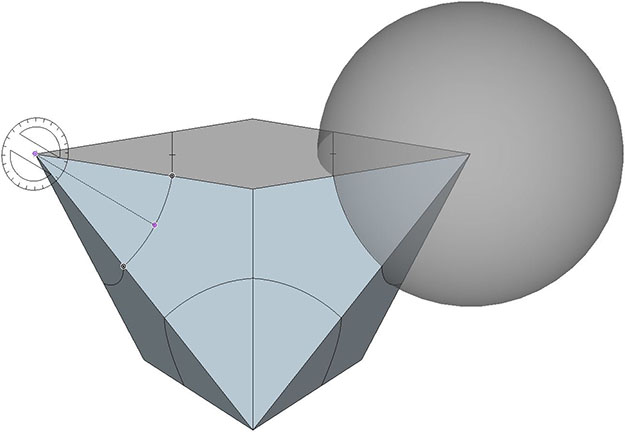
A ten-sided polyhedron constructed by connecting the vertices of two rhombuses, and scribed by arcs of radius r from each of its four acute corners.
A ten-sided polyhedron is constructed by connecting the vertices of the two rhombuses. Arcs scribed onto the faces from each of its four acute corners will be used to define the planes of its four large pentagonal faces.

The scribed arcs locate the peaks of the tetrakaidecahedron’s four larger pentagonal faces at A3, B3, C3 and D3 (see illustration).

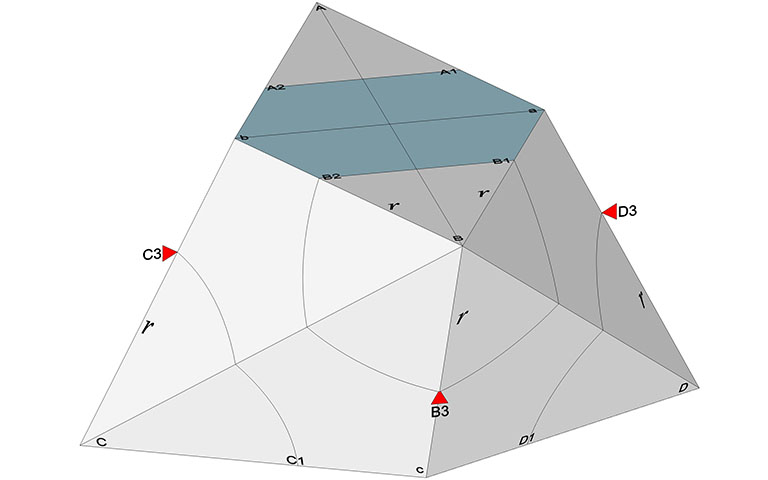
The ten-sided polyhedron from with the Weaire-Phelan tetrakaidecahedron will be constructed, scribed with points labeled.
The scribed arcs locate the peaks of the larger of the two pentagonal faces, indicated here by red triangles B3, C3, D3, and A3 (hidden).

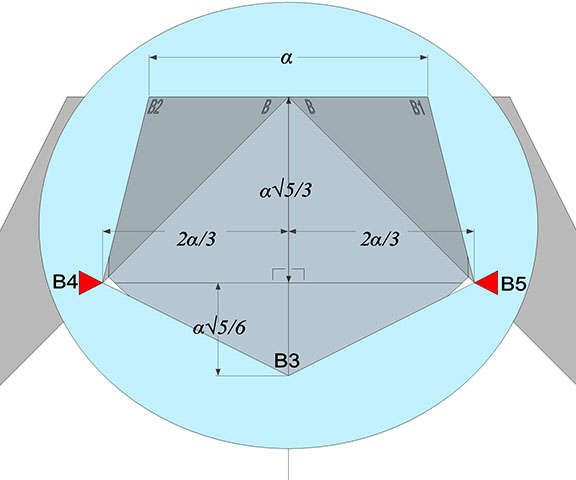
Each of the tetrakaidecahedron’s four larger pentagonal faces occupy a plane defined by the three vertices identified so far. At corner B, the plane (the blue disk in the illustration below) is defined by B1, B2, and B3. To locate the remaining two vertices, draw a line from the midpoint between B1–B2 to B3, and mark a point on this line ³√(√2/2)×√5/3 from the midpoint, or ³√(√2/2)×√5/6 from B3. A perpendicular through this point parallel to B1–B2 intersects BC and BD at B4 and B5, completing the pentagonal face (see illustration).

Illustration of the construction of the larger of the two pentagonal faces of the Weaire-Phelan tetrakaidecahedron.
The three points identified so far from corner B (B1, B2, and B3) define the plane (blue disk) occupied by the pentagonal face. This enables us to determine the positions of the pentagon’s remaining two vertices, B4 and B5. Note these points are not identical with the intersections of the arcs we scribed earlier, which lie slightly above the plane.

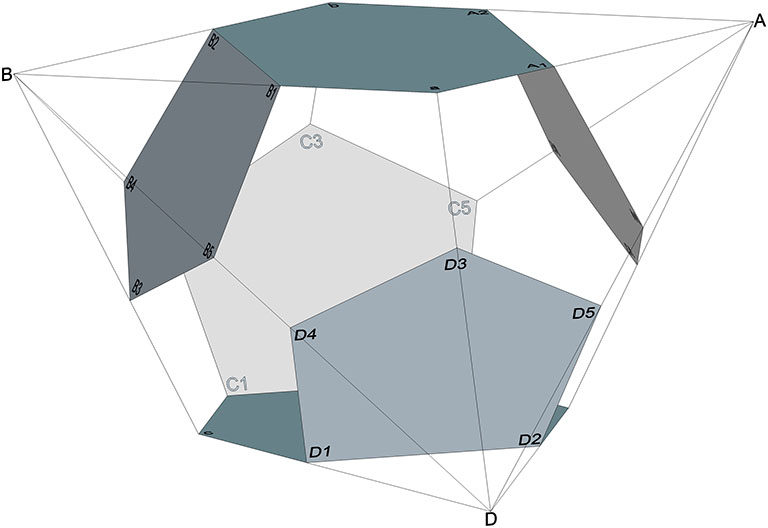
Repeating the steps for each corner A, B, C and D, produces four pentagonal faces in addition to the two hexagonal faces defined in the first step.

Six faces (two hexagons and four pentagons) of the Weaire-Phelan tetrakaidecahedron scribed onto the scaffold of a ten-sided polyhedon
The tetrakaidecahedron with its two hexagonal faces (top and bottom), and its four, larger pentagonal faces as constructed with the operations described.

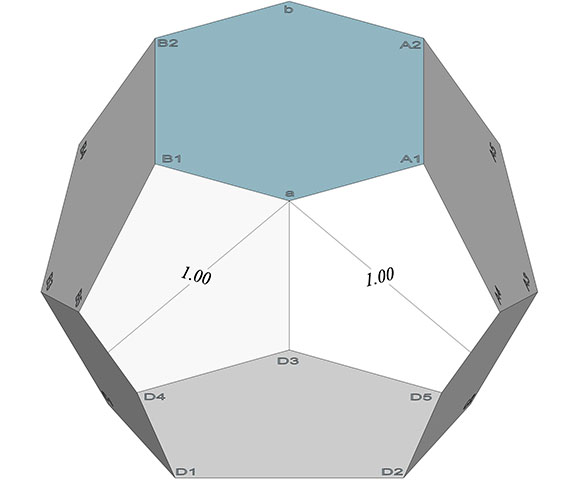
The points surrounding the remaining empty space should all lie on the same plane and define the eight smaller pentagonal faces of the Weaire-Phelan tetrakaidecahedron. A line bisecting their faces from the peak to mid-base should be of unit length, or, in terms of the isotropic vector matrix, one sphere diameter.

The Weaire-Phelan tetrakaidecahedron with vertices labeled and unit length indicated for the height of the smaller pentagonal faces.
The Weaire-Phelan tetrakaidecahedron. The height of its eight smaller pentagonal faces is identical with the diameter of the radially close-packed spheres that define the isotropic vector matrix.

Pyritohedron

Begin with three, intersecting and mutually perpendicular 1 x 2 rectangles all sharing a common center. To construct a pyritohedron that will complement the Weaire-Phelan tetrakaidecahedron to fill all-space, the rectangle’s short edge will be ³√(√2/2) and the long edge will be twice that length (see illustration).

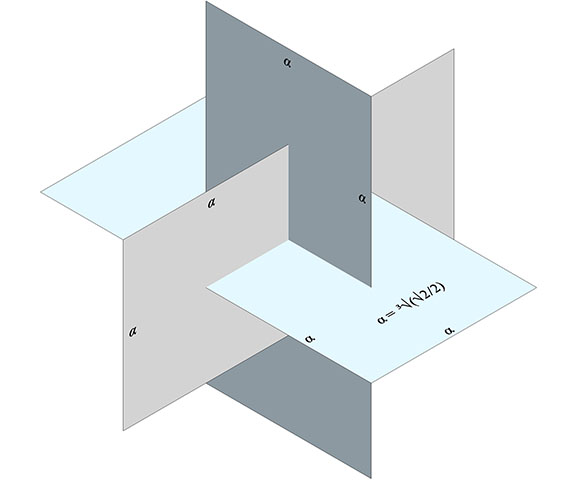
Three mutually perpendicular 1x2 rectangles to be used in constructing the pyritohedron.
The first step in the creation of the pyritohedon is to construct three mutually perpendicular 1×2 rectangles. The length of the short edge, α, is ³√(√2/2) and the long edge is 2×α.

The twelve pentagonal faces of the pyritohedron are identical with the four larger pentagonal faces of the tetrakaidecahedron, and they are constructed using a method nearly identical with the procedure for the four larger pentagonal faces of the tetrakaidecahedron described above. Each face plane is defined by the the short edge of one rectangle, and the nearest corners of the rectangle perpendicular to that edge.

Three mutually perpendicular 1x2 rectangles with one pentagonal face of the pyritohedron indicated by construction.
The twelve faces of the pyritohedron are constructed similarly to the larger of the pentagonal faces of the tetrakaidecahedron. The plane of each is defined the ends of the short edge of one rectangle and the nearest corners of the rectangle perpendicular to that edge.

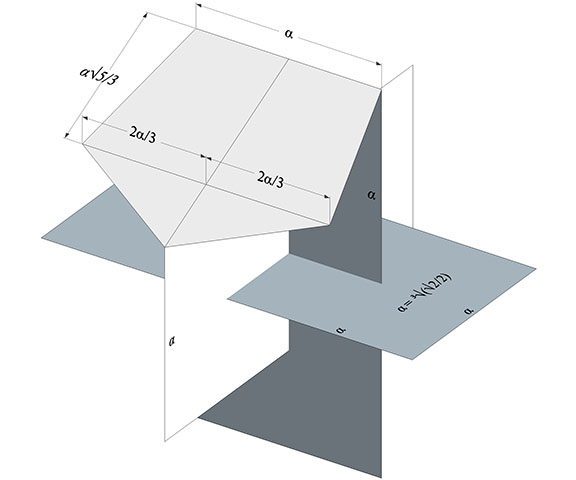
This pyritohedron has a rational volume of 24d³ in unit tetrahedra, where d is is the diameter of the unit sphere in the isotropic vector matrix or the height of the tetrakaidecahedron’s smaller pentagonal face. Its cubic volume of 4α³, where α is the length of the pyritohedron’s long edge. This volume should be identical with that of its companion tetrakaidecahedron. See Pyritohedron Dimensions and Whole-Number Volume, and Tetrakaidecahedron Dimensions and Whole Number Volume.

The pyritohedron with long edge equal to α = ³√(√2/2), and a volume of 24 unit tetraheda.
The pyritohedron. With the long edge equal to ³√(√2/2), it complements the Weaire-Phelan tetrakaidecahedron to fill all-space, and isolates the the nuclear domains of the radially-close-packed unit spheres of the isotropic vector matrix.

Leave a comment