The 31 Great Circles of the Icosahedron (new illustrations)

Greg Frederick

This is a supplement to a previous article, Great Circles: The 31 Great Circles of the Icosahedron, with new illustrations I hope will add clarity to the topic.

The figure below illustrates the full set of 31 great circles described by rotations about the regular icosahedron’s axes of symmetry.

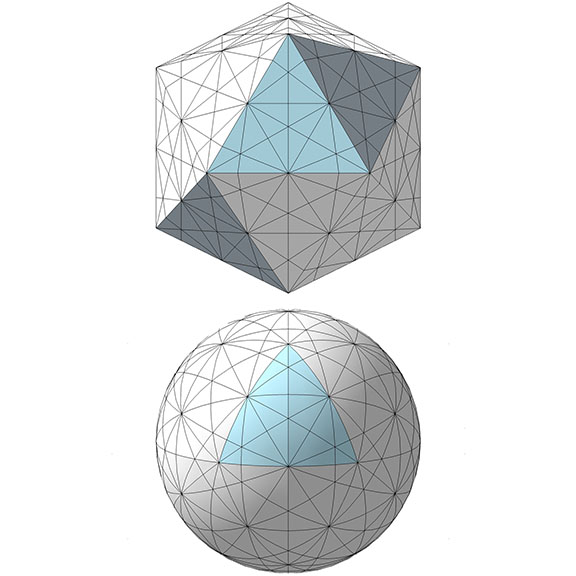
Illustration of the 31 great circles of the icosahedron projected onto the planar icosahedron (top), and sphere (bottom).
The 31 great circles of the icosahedron as projected onto the planar icosahedron (top) and sphere (bottom).

The 31 great circles are divided into three sets according to their spin axes. Axes running through diametrically opposing vertices generate the set of 6 great circles. Axes running through opposite faces generate the set of 10 great circles. And axes running through the midpoints of diametrically opposing edges generate the set of 15 great circles.

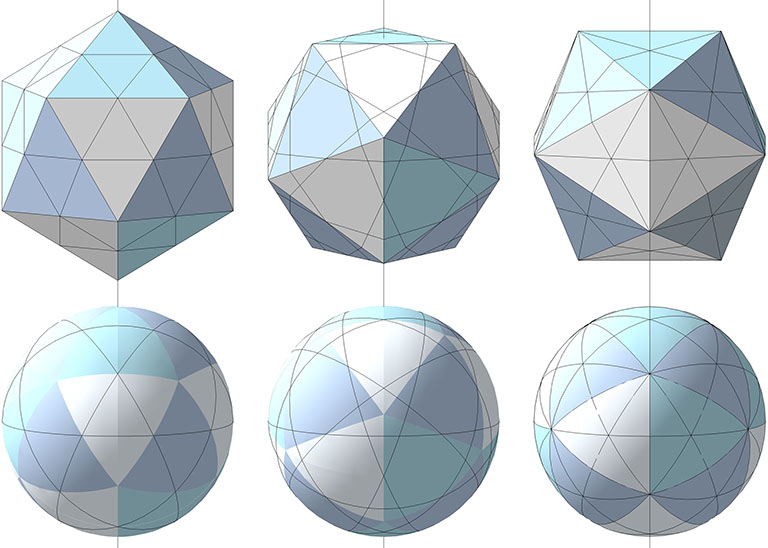
Illustration of the 3 sets of axes that define the 31 great circles of the icosahedron, as projected onto planar icosahedra (top) and spheres (bottom).
Left to right: the set of 6 great circles on axes running though opposing vertices; the set of 10 great circles on axes running through the centers opposing faces, and; the set of 15 great circles on axes running though he midpoints of opposing edges.

6 Great Circles

The set of 6 great circles circumscribes the equators of the six spin axes that pass through the icosahedron’s opposing vertices, and together they disclose the spherical icosidodecahedron.

Illustration of the set of 6 great circles of the icosahedron, and highlighted to disclose the spherical icosidodecahedron.
The set of 6 great circles of the icosahedron disclose the spherical icosidodecahedron.

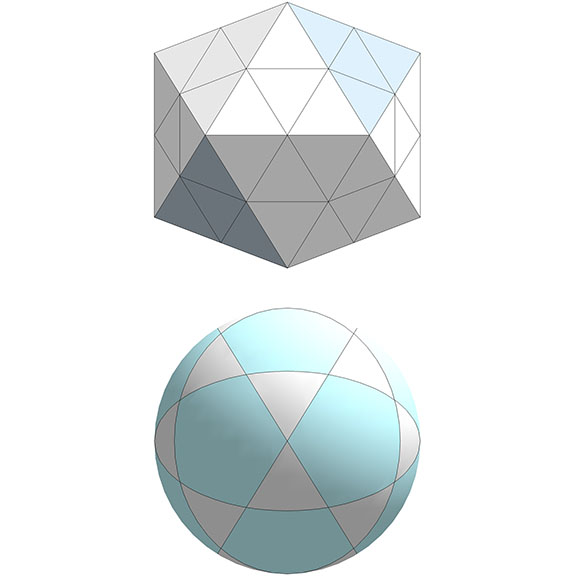
15 Great Circles

The set of 15 great circles disclose the two orientations of the spherical octahedron, the spherical icosahedron, pentagonal dodecahedron, rhombic triacontahedron, and the 120 basic disequilibrium LCD triangles.

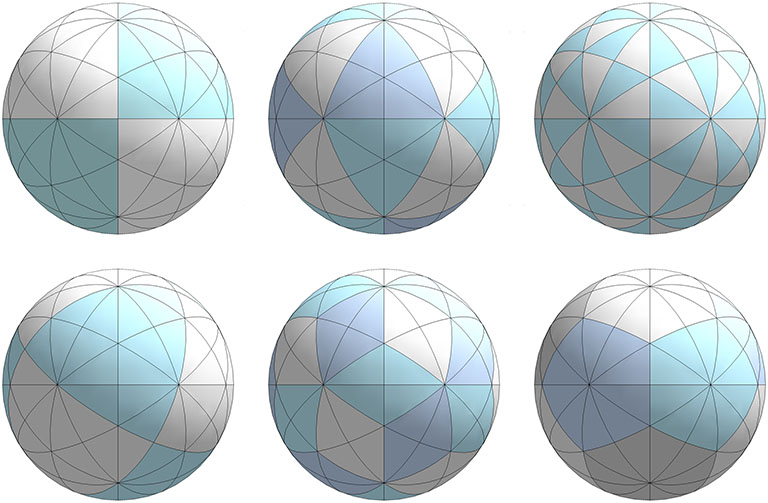
Illustration of the 15 great circles of the icosahedron, and highlighted to disclose two orientations of the spherical octahedron (left); spherical icosahedron (top middle); spherical rhombic triacontahedron (bottom middle); the 120 basic disequilibrium LCD triangles (top right); and spherical pentagonal dodecahedron (bottom right).
The set of 15 great circles of the icosahedron disclose two orientations of the spherical octahedron (left); the spherical icosahedron (top middle); the rhombic triacontahedron (bottom middle); the 120 basic disequilibrium LCD triangles (top right); and the pentagonal dodecahedron (bottom right).

The same spherical icosahedron is symmetrically aligned with both orientations of the spherical octahedron. See also: Icosahedron Inside Octahedron.

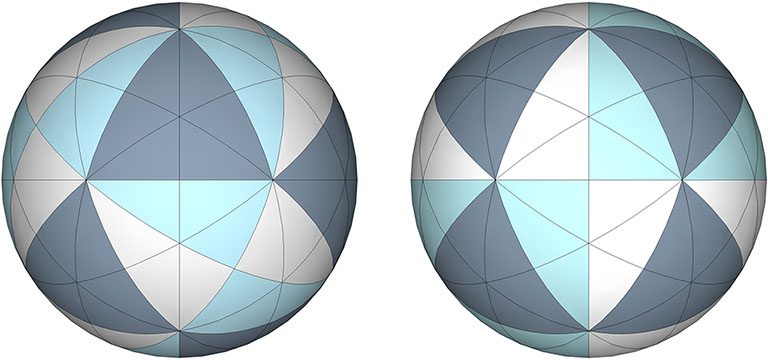
Illustration of the two orientations of the spherical octahedron with their faces inscribed with faces of the same spherical icosahedron as disclosed by the set of 15 great circles of the icosahedron.
Both orientations of the spherical octahedron align symmetrically with the same spherical icosahedron disclosed by the 15 great circles of the icosahedron.

10 Great Circles

The set of 10 great circles discloses three orientations of the spherical vector equilibrium (VE).

Illustration the set of 10 great circles of the icosahedron, and highlighted to disclose three orientations of the vector equilibrium (VE).
Three orientations of the vector equilibrium (VE) as disclosed by the 10 great circles of the icosahedron.

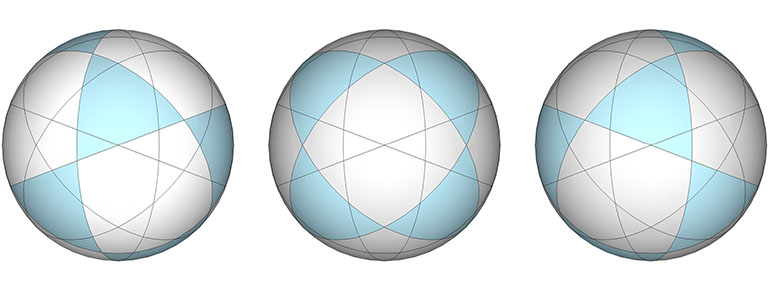
The same spherical icosidodecahedron (generated from the six great circles) is symmetrically aligned with all orientations of the spherical vector equilibrium (VE).

Illustration of the three orientations of the spherical vector equilibrium (VE) as disclosed by the 10 great circles of the icosahedron, and highlighted to disclose their alignment with spherical icosidodecahedron (disclosed by the set of 6 great circles of the icosahedron.)
All three orientations of the VE as disclosed by the 10 great circles of the icosahedron are symmetrically aligned with the same icosidodecahedron disclosed by the 6 great circles.

Leave a comment