The 25 Great Circles of the VE (new illustrations)

Greg Frederick

This is a supplement to a previous article, Great Circles: The 25 Great Circles of the Vector Equilibrium (VE), with new illustrations which I think add some clarity to the topic.

The figure below illustrates the full set of great circles in the context of the vector equilibrium (VE), both the planar VE (top), and spherical VE (bottom). Note that twelve great circles converge, cross, or are deflected at each of the twelve vertices, and at the centers of each triangular face.

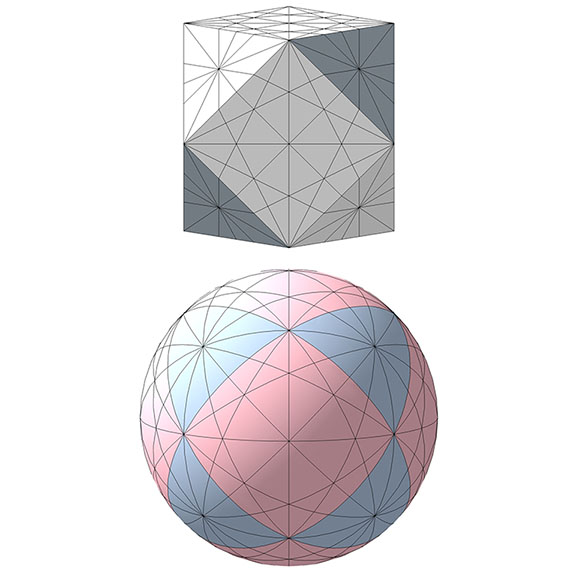
The 25 great circles of the vector equilibrium (VE) projected onto the surface of a planar VE (top) and a spherical VE (bottom).
The 25 great circles of the vector equilibrium (VE)

The 25 great circles are divided into four sets according to their spin axes. Axes running through opposite square faces generate the set of 3 great circles. Axes running through the centers of opposite triangular faces generate the set of 4 great circles. Axes running through diametrically opposing vertices generate the set of 6 great circles. And axes running through the midpoints of diametrically opposing edges generate the set of 12 great circles.

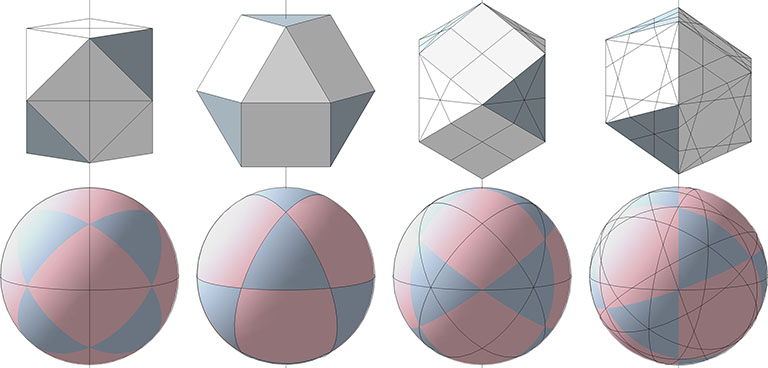
The 25 great circles of the vector equilibrium (VE) divided into four sets according their spin axis, illustrated with both planar and spherical VEs.
Left to right: Set of 3 great circles on axes through opposing square faces; Set of 4 great circles on axes running through opposing triangular faces; Set of 6 great circles on axes running through opposing vertices; Set of 12 great circles with axes running through opposing edges.

3 Great Circles

The set of 3 great circles discloses the spherical octahedron.

Illustration of a spherical octahedron.
The spherical octahedron disclosed from the set 3 great circles, with one face highlighted.

4 Great Circles

The set of 4 great circles discloses the spherical vector equilibrium (VE).

Illustration of a spherical vector equilibrium (VE).
The spherical VE disclosed from the set of 4 great circles, with its triangular faces highlighted.

6 Great Circles

The six great circles disclose the spherical rhombic dodecahedron, the spherical tetrahedron (both positive and negative), and the spherical cube.

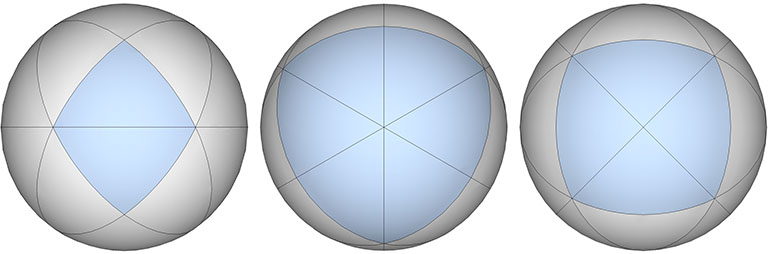
Illustrations of a spherical rhombic dodecahedron, tetrahedron, and cube derived from the 6 great circles of the vector equilibrium (VE).
The set of 6 great circles disclosing, left to right: the spherical rhombic dodecahedron; the spherical tetrahedron, and; the spherical cube, each with one face highlighted.

The six great circles complement the three great circles to disclose three additional octahedra.

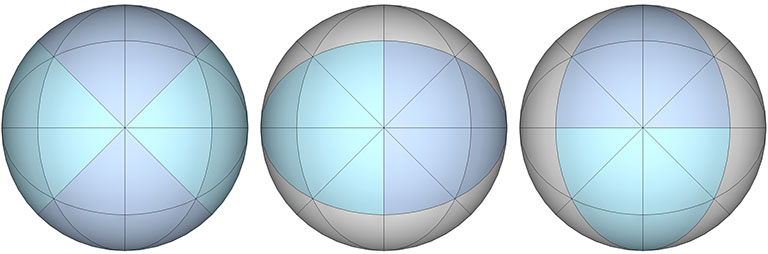
Three spherical octahedra with the primary axis perpendicular to viewer (left), horizontal (middle), and vertical (right).
The sets of 3 and 6 great circles disclose three additional spherical octahedron.

The same combination of great circles (3 and 6) also disclose the perimeter of the basic equilibrium LCD triangle.

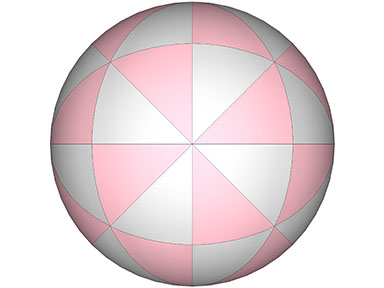
Sphere divided into 48 identical triangles, the basic equilibrium LCD triangle.
The sets of 3 and 6 great circles of the VE disclose the 48 basic equilibrium LCD triangles.

12 Great Circles

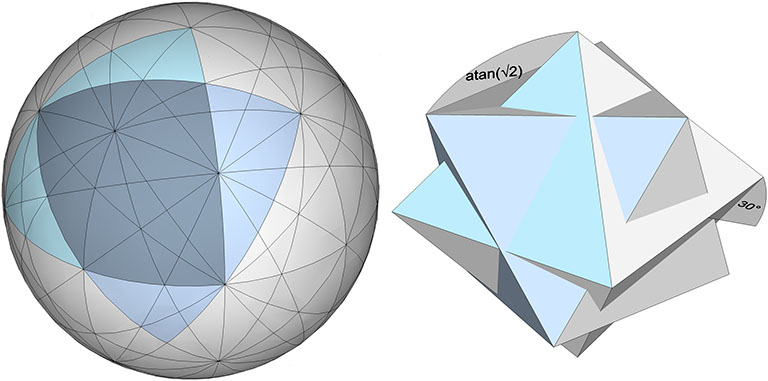
The twelve great circles of VE do not appear to disclose, by themselves, any of the regular polyhedra. However, in combination with the 4 and 6 great circle sets, the 12 great circles do disclose an alternate spherical regular octahedron that is curiously askew from the others, rotated 30° on the z axis, and atan(√2) on the y axis.

The 25 great circles of the VE (left) disclose the regular octahedron (light blue), and an alternate octahedron (violet) that is rotated 30° on the z axis, and atan(√2) degrees on the y axis, illustrated with overlapping planar octahedron (right).
The 4, 6, and 12 great circles of the VE each contribute one edge to disclose a spherical octahedron whose axes are curiously skewed from all the other polyhedra the 25 great circles of the VE disclose.

Leave a comment