Spaces and Spheres (Redux)

Greg Frederick

“The closest-packed symmetry of uniradius spheres is the mathematical limit case that inadvertently captures all the previously unidentifiable otherness of Universe whose inscrutability we call space. The closest-packed symmetry of uniradius spheres permits the symmetrically discrete differentiation into the individually isolated domains as sensorially comprehensible concave octahedra and concave vector equilibria, which exactly and complementingly intersperse eternally the convex “individualizable phase” of comprehensibility as closest-packed spheres and their exact, individually proportioned, concave-in-betweenness domains as both closest packed around a nuclear uniradius sphere or as closest packed around a nucleus-free prime volume domain.”
—R. Buckminster Fuller, Synergetics, 1006.12

Spaces, like spheres, have surfaces. The interstitial model of the isotropic vector matrix (IVM) makes evident that it is the sphere’s surfaces (both its convex and its concave surfaces) that matter. Electric charge is carried on the surface of the conductor. Molecular biology is all about the lock and key system of protein surfaces and shapes. The surface of the “space” in the isotropic vector matrix is a continuity broken only be the seams at the interface of the concave “spaces” and “interstices” (see below). These seams align with the four great circles of the vector equilibrium (VE), and describe the most efficient paths between the points of contact with adjacent spheres. See also: Anatomy of a Sphere.

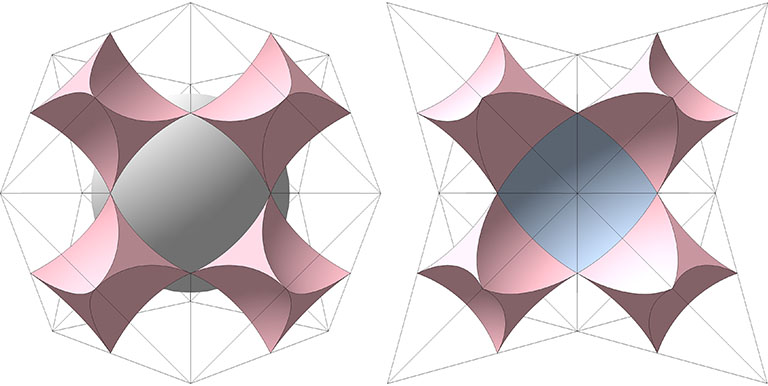
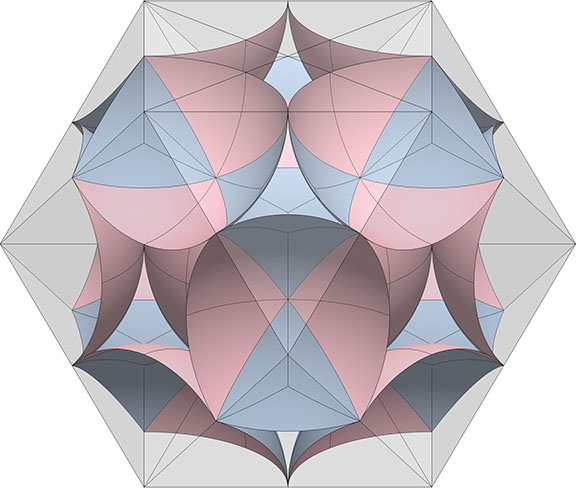
The figure below shows the exact correlation between two models of the isotropic vector matrix, a correspondence that Fuller attempted to describe in the excerpt I’ve quoted above.

The packing of concave octahedra, concave vector equilibria, and spherical vector equilibria (right) corresponds exactly to the space filling of planar octahedra and planar vector equilibria (left).
Space Filling of Octahedron and Vector Equilibrium: The packing of concave octahedra, concave vector equilibria, and spherical vector equilibria corresponds exactly to the space filling of planar octahedra and planar vector equilibria. Exactly half of the planar vector equilibria become convex; the other half and all of the planar octahedra become concave.

Though the VEs (blue) and octahedra (pink) on the left align with the spaces (blue) and interstices (pink) on the right, close inspection of the above models reveals a key difference. The model on the left does not distinguish between spheres and spaces. While on the right the difference is obvious, on the left both spheres and spaces are represented by identical VEs. The ambiguity is apt: In the isotropic vector matrix, there is a one-to-one identity between the spheres and spaces; one is simply the other turned inside out.

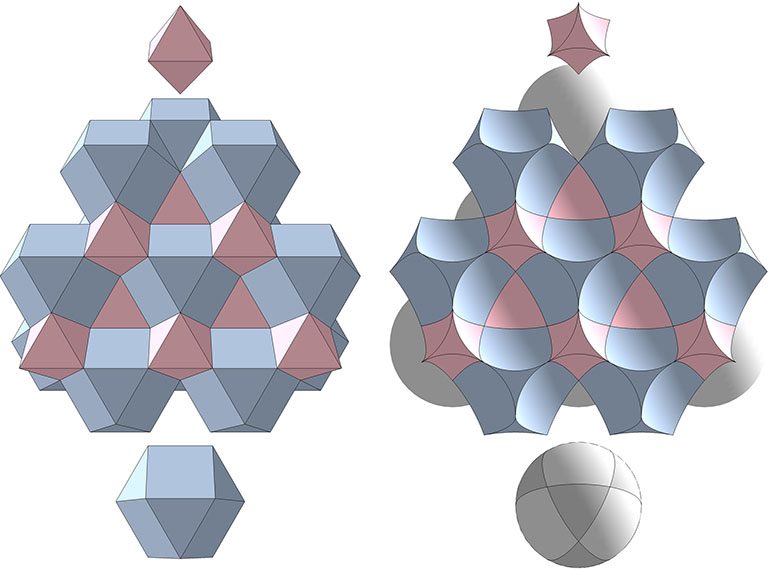
The model on the right is what I’m calling the interstitial model of the isotropic vector matrix. It consists of concave vector equilibrium (VE) spaces and concave octahedron interstices. The concave VE is the shape of the void at the center of six close-packed spheres defining the octahedron. The concave octahedron is the shape of the void at the center of four close-packed spheres defining the tetrahedron.

Concave VE (“space”)

Because it occupies the space in the isotropic vector matrix that is replaced by a sphere in the jitterbug transformation, I reserve the term “space” for the concave VE at the common center of the six close-packed spheres of the regular octahedron.

Illustration of the concave-VE-shaped void at the center of six close-packed spheres centered on the vertices of the regular octahedron.
The void at the center of the six close-packed spheres centered on the vertices of the regular octahedron has the shape of a concave vector equilibrium (VE). In the jitterbug transformation, this “space” is turned inside-out to define the spherical VE or “sphere.”

Concave Octahedron (“interstice”)

The void at the center of four close-packed spheres has the shape of a concave octahedron which I call the “interstice” to distinguish it from the “space” referred to above. The interstices maintain both their shape and position during the jitterbug transformation, while their 90° rotations articulate the sphere-to-space oscillations described below.

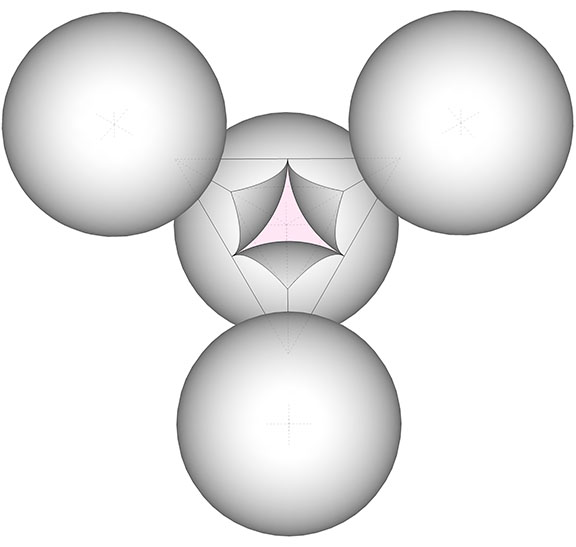
Illustration of the concave-octahedra-shaped void at the center of the six spheres centered on the vertices of the regular tetrahedron.
The void at the center of the four spheres centered on the vertices of the regular tetrahedron has the shape of a concave octahedron. These “interstices” are rotated 90° to alternately define the spheres and spaces that exchange places in the jitterbug transformation.

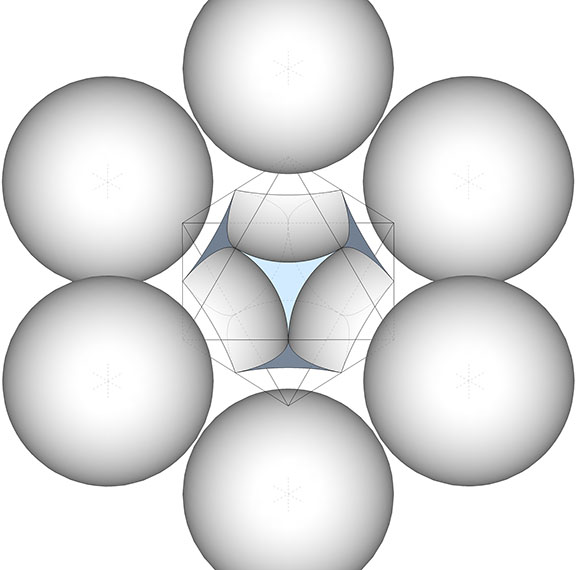
Spherical Domains

The polyhedra of the isotropic vector matrix divide the spheres into rational sections which, when added together, constitute the polyhedron’s spherical domain. Fuller thought this rationality was sufficient to eliminate pi (π) from his geometry. He’d already shown that the volumes of most polyhedra were rational if instead of the cube we used the regular tetrahedron as the unit volume. And if we replaced the irrational volume of the sphere with the rational sections carved from the rational polyhedra, pi was irrelevant.

Rhombic Dodecahedron144 quanta modules1 spherical domain
Vector Equilibrium (VE)480 quanta modules3.40 spherical domains
Cube72 quanta modules1/2 spherical domain
Octahedron96 quanta modules3/5 spherical domain
Tetrahedron24 quanta modules1/5 spherical domain

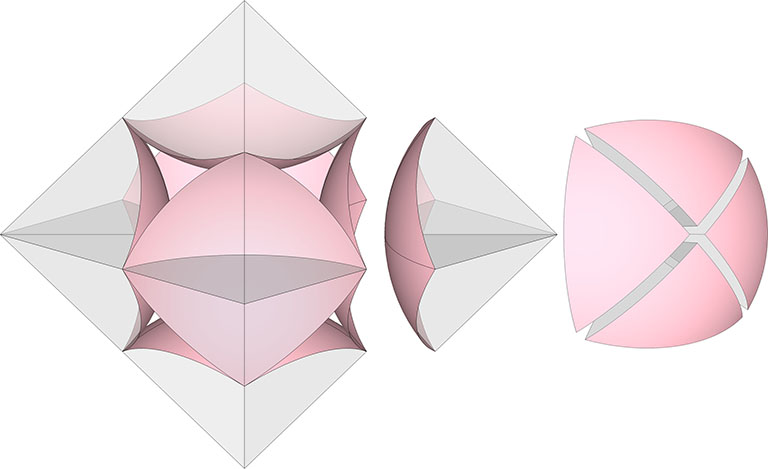
Octahedron

The six spheres at the vertices of the octahedron define the concave vector equilibrium space at its center. The planar facets of each vertex carve a 1/10 section from its sphere. The 1/10 section is further subdivided to form the four 1/40 sections used in the spherical domain calculations. The total spherical domain of the planar octahedron is 3/5.

Illustration of the concave-VE space divided into six 1/10th spheres whose centers are at the vertices of a regular octahedron. One of these sections has been further subdivided into four equal sections along the diagonals of the convex square face.
The planar octahedron cuts 1/10 sections from each of its six spheres, for a total spherical domain of 3/5. Each of these 1/10 sections is further subdivided into four 1/40 sections which are used to calculate the spherical domains of the remaining polyhedra.

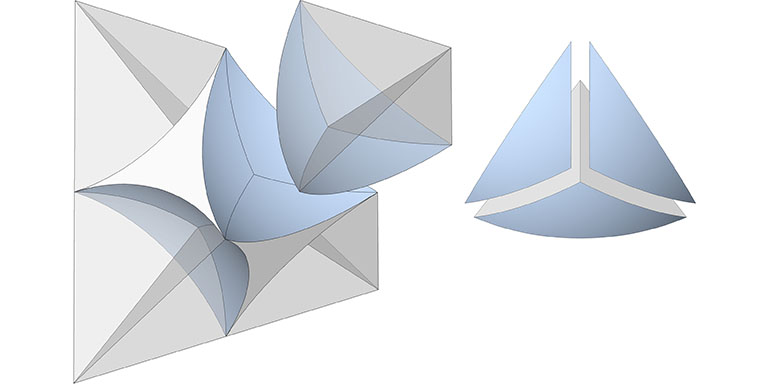
Tetrahedron

The four spheres at the vertices of the tetrahedron define the concave octahedron interstice at its center. The planar facets of each vertex carve a 1/20 section from its sphere. The 1/20 section is further divided to form the three 1/60 sections used in the spherical domain calculations. The total spherical domain of the planar tetrahedron is 1/5.

Illustration of the concave-octahedron space divided into four 1/20th spheres whose centers are at the vertices of a regular tetrahedron. One of these sections has been further subdivided into three equal sections along lines connecting the center of the convex triangular face with its three vertices.
The planar tetrahedron cuts 1/20 sections from each of its four spheres, for a total spherical domain of 1/5. Each of these 1/20 sections is further subdivided into three 1/60 sections which are used to calculate the spherical domains of the remaining polyhedra.

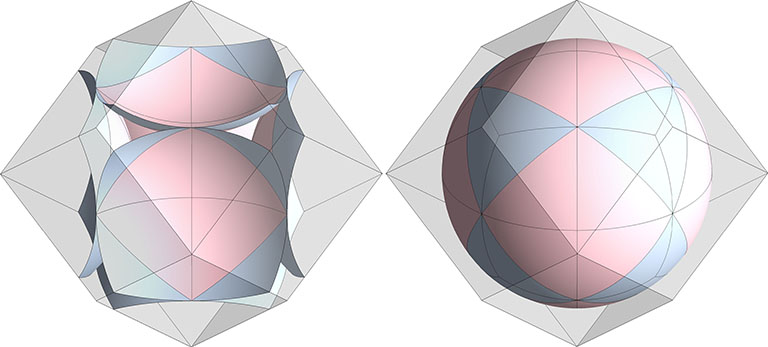
Rhombic Dodecahedron

There are two rhombic dodecahedra in the isotropic vector matrix—one with a space at its center, and one with a sphere. For the rhombic dodecahedron with a space at its center, each of the six acute vertices define the center of a sphere from which the planar facets of each carve a 1/6 section. Both of the planar rhombic dodecahedra contain precisely one spherical domain.

Note that one is made from the other by reversing the 1/6 sections so that their peaks point either inward to define the sphere, or outward to define the space.

Two planar rhombic dodecahedra, one defining the domain of a concave VE space and the other the convex VE domain of sphere in the context of the isotropic vector matrix.
The planar rhombic dodecahedron on the left cuts 1/6 sections from each of the six spheres centered on its six acute vertices, for a total spherical domain of 1, the same spherical domain of the rhombic dodecahedron on the right, where the 1/6 sections have been rotated 180° so that their convex faces are pointing outward.

Cube

There are two cubes in the isotropic vector matrix, one a 90° rotation of the other. Their rotation comprises the jitterbug transformation and the exchange between spheres and spaces. Four of its eight vertices each define the center of a sphere from which the planar facets of each carve a 1/8 section. The planar cube contains precisely 1/2 spherical domain.

Two planar cubes, one a 90° rotation of the other, showing them each to be comprised of four 1/8 sections of a sphere.
The planar cube carves a 1/8 section from the spheres centered on four of its eight vertices, for a total spherical domain of 1/2. The cube on the right is a 90° rotation of the cube on the left. This rotation accounts for the sphere-to-space oscillations of the isotropic vector matrix in the jitterbug transformation.

Vector Equilibrium (VE)

The twelve vertices of the VE each define the center of a sphere from which the planar facets carve a 1/5 section. These plus the nuclear sphere add to a total of 3.4 spherical domains.

The planar vector equilibrium (VE) comprised of twelve 1/5 sphere sections and one nuclear sphere.
The planar vector equilibrium (VE) carves 1/5 sections from each of the twelve spheres centered on its vertices. These plus the nuclear sphere total add to 3.4 spherical domains.

Ratio of Spheres to Spaces in the Isotropic Vector Matrix

While the sphere-to-space ratio differs for the polyhedra, when the isotropic vector matrix is considered as a whole the ratio approaches that of the rhombic dodecahedron; rhombic dodecahedra close pack exactly as spheres close pack, and the rhombic dodecahedron constitutes one spherical domain.

The volume of the unit-diameter sphere is π√2 tetrahedra and the volume of the rhombic dodecahedron which contains that sphere is six unit tetrahedra. So, the sphere-to-space ratio is (π√2)/(6 – π√2), or ≈ 2.853275. Fuller wanted this number to be rational. It is not.

Transparency showing the rhombic dodecahedron domain of the unit-diameter sphere.
The domain of the radially close-packed unit-diameter sphere is a rhombic dodecahedron whose in-sphere radius and long face diagonal are of unit length, and whose tetrahedral volume is exactly 6.

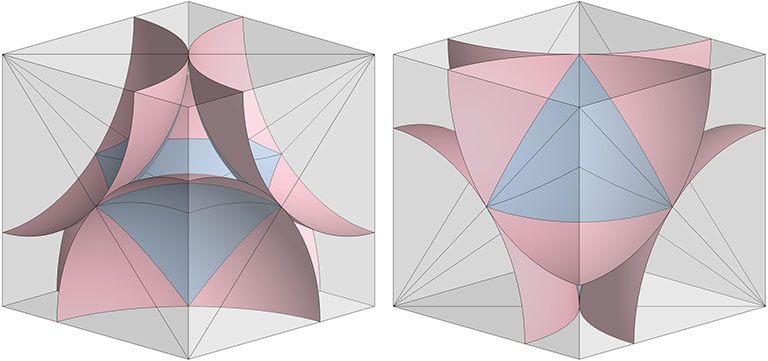
Sphere-to-Space and Space-to-Sphere Oscillation of the Jitterbug

The interstitial model provides the most literal interpretation of the space-to-sphere oscillations of the jitterbug. The tetrahedron’s polarity reversal is accomplished by a 90° rotation of the concave octahedron interstices which alternately disclose the nuclear sphere, on the left in the illustration below, and the nuclear space, on the right:

On the left, the vector equilibrium constructed of eight concave octahedron interstices framing its nuclear sphere. On the right, the concave octahedron interstices of been rotated 90° to frame a concave VE space at the center of a regular octahedron.
The concave octahedron interstices are rotated 90° to alternately disclose the nuclear sphere at the center of the vector equilibrium (left), and the nuclear space at the center of the octahedron (right).
An animated model of the jitterbug, with sixteen concave octahedra rotating 90° to alternately disclose one sphere and two concave VE spaces, and two spheres and one concave VE space.
The 90° rotation of the concave octahedra interstices at the centers of positive and negative tetrahedra account for the sphere-space oscillations of the jitterbug transformation.

Leave a comment