A curious mathematical coincidence that I think is worth noting is that the edge length of the tetrahedron in which a unit octahedron or unit icosahedron is inscribed is numerically equivalent to the units of volume, in tetrahedra, provided by each of the inscribed polyhedron’s structural quanta. (For more information on calculating volumes in tetrahedra, see Areas and Volumes in Triangles and Tetrahedra.)
A structural quantum is defined by the six edges of the minimum structural system. The six edges of the tetrahedron comprise one structural quantum, the twelve edges of the octahedron comprise two structural quanta, and the thirty edges of the icosahedron comprise five structural quanta.
In the regular tetrahedron, one structural quantum encloses 1 unit of volume. In the regular octahedron, one structural quantum encloses 2 units of volume. And, in the regular icosahedron, one structural quantum encloses Φ²√2 units of volume (where Φ is the golden ratio: (√5+1)/2).
If these unit polyhedra (i.e., all edges are of unit length) are inscribed within a regular tetrahedron, the edge length of the enclosing tetrahedron is numerically equivalent to the volume enclosed by each structural quantum of the inscribed polyhedron.

Fuller’s “structural quanta” are related to the idea that all the structural polyhedra can be thought of as self-interfering wave patterns. Each cycle of the wave consists of the three vectors of an open ended triangle. The tetrahedron, for example, consists of two open-ended triangles, one clockwise and one counter-clockwise, as in the following illustration:
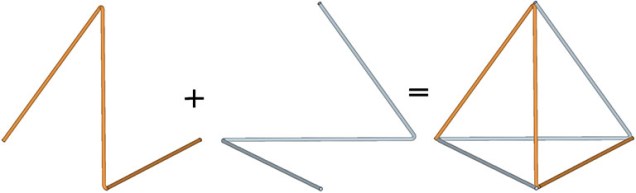
The six vectors of the two open-ended triangles constitute one “structural quantum.” See also: Isotropic Vector Matrix as Transverse Waves.