Tensegrity Sphere Equations

Greg Frederick

I’ve used the equations described in this topic to calculate the strut and tendon lengths of the tensegrity sphere models I describe in Model Making. They are slightly modified from those published by Hugh Kenner in his book, Geodesic Math and How To Use It (1976, 2003). See also: Tensegrity.

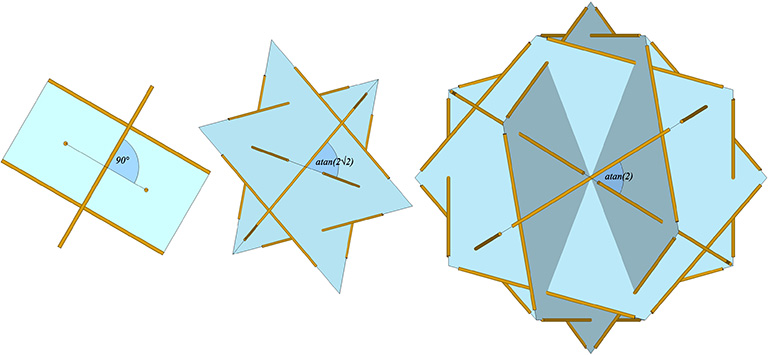
After some rather clever reasoning, Kenner concluded that all of the dimensions of the tensegrity spheres could be derived from just two quantities: the number of sides (n) in their great circle (or lesser circle) planes, and the angle (µ) at which they cross. The following illustration shows the three primary tensegrity spheres, i.e., the spherical phases of the tensegrity tetrahedron, octahedron, and icosahedron:

  • the six-strut tensegrity sphere with three great circles planes of two struts (n=2), each crossing at µ=90°;
  • the twelve-strut tensegrity sphere with four great-circle planes of three struts (n=3), each crossing at µ=atan(2√2) ≈ 70.530°; and,
  • the thirty-strut tensegrity sphere with six great circle planes of five struts (n=5), each crossing at µ=atan(2) ≈ 60.435°.
The intersecting great circle planes of the (from left to right) six-, twelve-, and thirty-strut tensegrity spheres, intersecting at 90°, arctan(2√2) and arctan(2), respectively.
The great circle planes of the six-, twelve-, and thirty-strut tensegrity spheres, and the angles at which they intersect

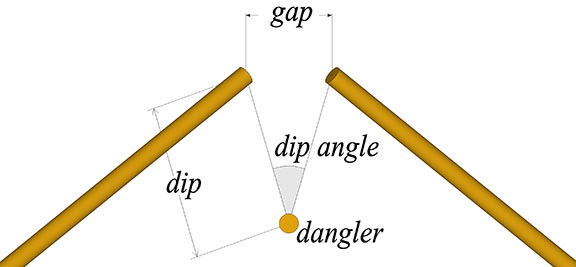
The intersection of the great-circle and lesser-circle planes can be broken down to two struts and a dangler, as in the following illustration.

The ends of two struts of a tensegrity sphere straddling their dangler strut, with "gap", "dip", and "dip angle" identified.
The gap, dip, and dip angle are parameters used in the calculations for tensegrity structures.

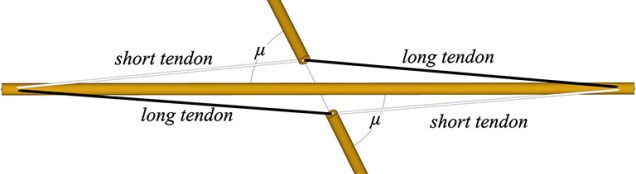
The dangler strut’s great circle crosses the great circle of the other two struts at an angle, µ. If this angle is less than 90° (as is the case for all but the six-strut tensegrity sphere), the tension elements will consist of a long and a short tendon, as shown in the following illustration.

Two struts of a tensegrity sphere crossing the midpoint of their dangler at angle, µ, with long and short tendons identified.
Two struts of a great circle plane crossing the midpoint of a dangler at angle, µ, with the long and short tendons connecting their endpoints.

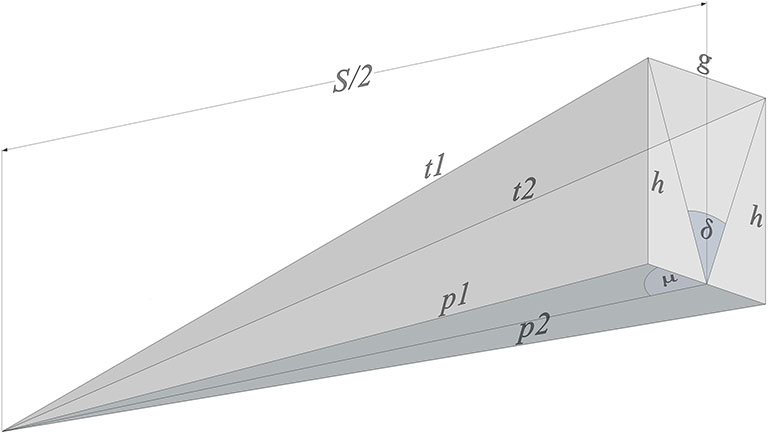
The next illustration shows the relationships between all the parameters that go into calculating the circumsphere radius, strut length, and tendon lengths of the tensegrity spheres:

  • S = strut length;
  • r = the circumsphere radius, from sphere center to each of the strut endpoints;
  • dangler = the strut bisected by the great circle plane of two struts;
  • μ = the angle the great circle plane of the dangler makes with the great circle plane of the two struts;
  • d = dip, i.e., the distance between each strut’s endpoint and the midpoint of its dangler;
  • δ = the dip angle, i.e., the angle between the dangler’s midpoint and the two strut endpoints;
  • g = the gap, i.e. the linear distance between the two strut endpoints;
  • h = the vertical distance between a strut’s endpoint and the horizontal plane of its dangler;
  • t1 and t2 = the length of the short and long tendons, respectively;
  • p1 and p2 = the base of the right angle made with h, and with t1 or t2 as its hypotenuse, respectively.
Illustration of relationships between the parameters used to calculate the dimensions of a tensegrity sphere.
Parameters and equations used to calculate the tendon lengths (t1 and t2) of the three primary tensegrity spheres.

The Equations

  • S = strut length
  • dip angle (δ) = 180°/n
  • gap (g) = S×sin²(δ/2)
  • dip (d) = S×sin(δ/2)/2 = √g/2
  • height (h) = √((g–g²)/4)
  • p1 = √[(S/2)²+(g/2)²+((S/2)×g×cos(µ))]
  • p2 = √[(S/2)²+(g/2)²- ((S/2)×g×cos(µ))]
  • short tendon (t1) = √(h²+p1²)
  • long tendon (t2) = √(h²+p2²)
  • circumsphere radius (r) = √((1+3g)/16g)

Leave a comment