The Jessen Orthogonal Icosahedron in the Isotropic Vector Matrix

Greg Frederick

The Jessen Orthogonal Icosahedron fits neatly between two overlapping vector equilibria (VEs) in the isostropic vector matrix.

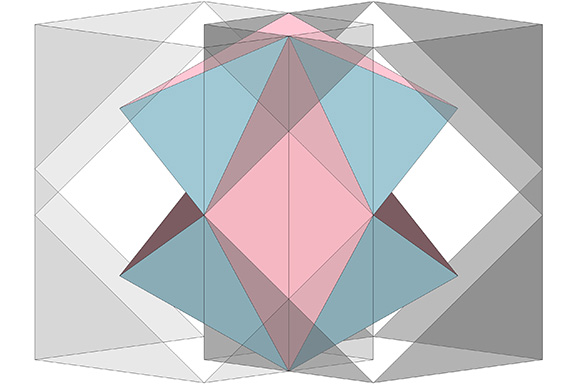
The Jessen Orthogonal Icosahedron placed between two symmetrically overlapping vector equilibria (VEs)
The Jessen Orthogonal Icosahedron (center) constructed from two overlapping VEs (left and right).
Click on image to open animation in new tab.

This is halfway between the nuclear sphere at the center of the VE and the space at the centers of its constituent octahedra. The location is apt, as the Jessen marks the halfway point in the jitterbug transformation between the VE and octahedron, i.e., between spheres and spaces.

Schematic showing the relative placement of the Jessen Orthogonal Icosahedron between a VE with a sphere at its center, and an octahedron with a space (concave vector equilibrium) at its center.
The Jessen Orthogonal Icosahedron (blue) occupies a position in the isotropic vector matrix diametrically halfway between the spheres and spaces at the centers of VEs and octahedra in the isotropic vector matrix.

The Jessen has a rational tetrahedral volume. If we attempt to isolate the space it occupies in the quanta module construction of the isotropic matrix, we discover that it can almost, but not entirely be modeled in A and B quanta modules.

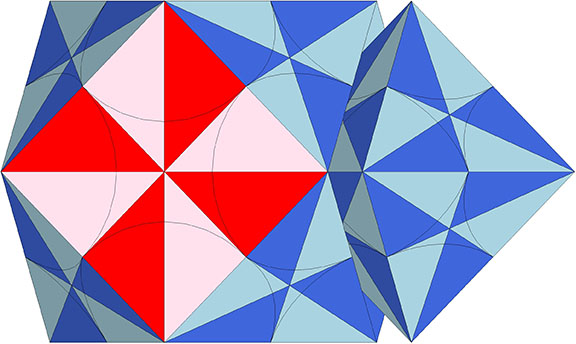
Quanta module construction of a vector equilibrium (VE) and one of its constituent octahedra.

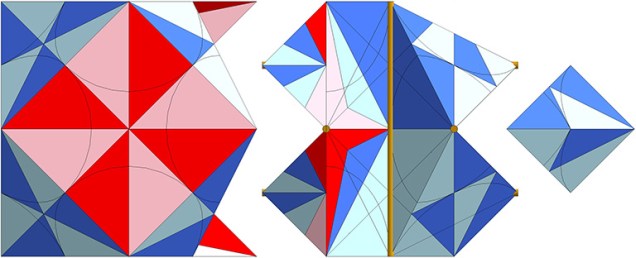
A and B Quanta module construction of a vector equilibrium (VE) and one of its constituent octahedra, animated to reveal a partial construction of the Jessen Orthogonal Icosahedron at their center.
The position of the Jessen Orthogonal Icosahedron in the quanta module construction of the isotropic matrix.
Click on lower image to open animation in new tab.

At the center of the quanta module construction of the Jessen is the eight-Mite coupler that joins spheres with spaces.

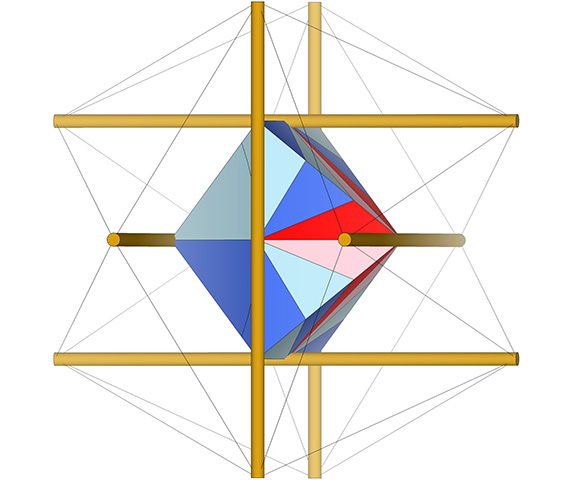
Six-strut tensegrity sphere with a with the four-Mite, sphere-space coupler at its center.
An eight-Mite coupler lies the center of the Jessen Orthogonal Icosahedron, shown here as the six-strut tensegrity sphere whose struts and tendons define the Jessen’s edges.
Click on image to view animation in new tab.

Note that the coupler is polarized and seems to point, forwards and backwards, along the vector of its displacement between the VE and octahedron, i.e. from the sphere in the direction of its adjoining space (or vice versa). The only other polyhedron whose quanta module construction is similarly polarized is the cube. The orientation of the cube in the quanta module construction of the isotropic vector matrix determines the polarity of the tetrahedron, and the six-strut tensegrity that defines the Jessen is the spherical phase of the tensegrity tetrahedron, the wave function, if you will, that collapses into either a positive or negative tetrahedron. (See also: Dual Nature of the Tetrahedron.)

Leave a comment