*This article is under construction.

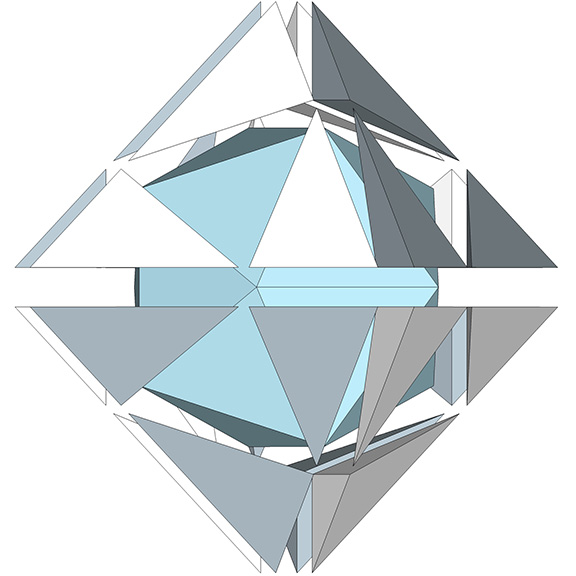
“The icosahedron positioned in the octahedron describes the S Quanta Modules. […] As skewed off the octa-icosa matrix, they are the volumetric counterpart of the A and B Quanta Modules as manifest in the nonnucleated icosahedron. They also correspond to the 1/120th tetrahedron of which the triacontahedron is composed.”
—R. Buckminster Fuller, Synergetics, 988.110

The S quanta module is documented in Synergetics, but it doesn’t seem to have led Fuller anywhere. It was, I think, an attempt to rationalize the volume of the icosahedron, or, at the very least, to calculate the volume of the icosahedron that is inscribed inside the regular octahedron. See Icosahedron Inside Octahedron. Fuller’s operational method is provided here, along with my own calculations which, it should be noted, don’t always agree with Fuller’s.

With a regular icosahedron placed inside a regular octahedron with unit-length edges, the space not occupied by the icosahedron is subdivided into 24 irregular tetrahedron, 12 positive and 12 negative. These are the S quanta modules.

With the edge of the octahedron, a, taken as unity, the six edges of the S quanta module have the following lengths:

AC = a(3-√5)/2;
CB = a/φ;
AC+CB = a = 1
BA = a√(7-3√5);
AD = a√(7-3√5)/2;
BD = a√3×√(7-3√5)/2, and;
CD = a√(7-3√5)/2

With the edge of the icosahedron, d, taken as unity, the six edges of the S quanta module have the following lengths:

AC = d√3/2
CB ≈ d×0.9045085
BA = d = 1
AD = d/2
BD = d√3/2
CD = d/2

Given the following angles:

α = atan(√15/3) + 30° ≈ 82.2387561°;
ß = atan(√15/5) ≈ 37.7612439°;
Φ = atan(√5/5) ≈ 24.0948426°, and;
Θ = atan(1+φ) ≈ 69.0948426°,

the vertices of the S quanta module are:

A (45°,α, 45°);
B (30°, ß, Φ);
C (45°,60°,45°), and;
D (90°, 90°, (180°- Θ))

Note that the difference of 90° and α (i.e. 90°−82.2387561°) is 7.7612439°, or arctan(√(3/5))-30°. (See angle n in figure below.) This is the same angle that separates the icosahedron phases of the jitterbug.

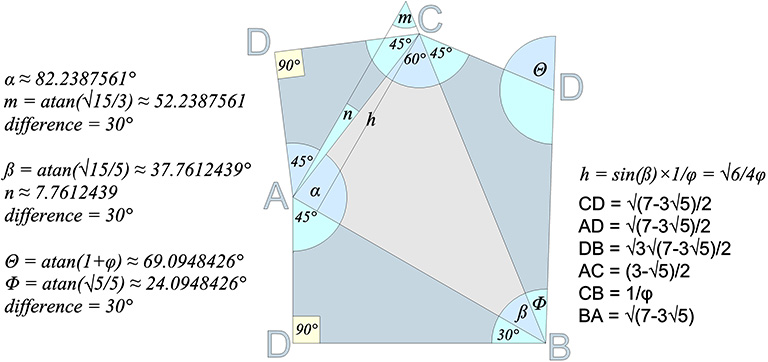
To calculate the volume of the S quanta module, we first find the area of its external face which will be taken as the S module’s base.

Base of external face of S module = BA
= a√(7-3√5) = d
90° height of external face of S module = h
= sin(ß) × BC = √6/4 × a/φ ≈ √6/4 × d×0.9045085
60° height of external face of S module = h’ = h × 2√3/3
= a√6/4φ × 2√3/3 = a√2/2φ ≈ √6/4 × d×0.9045085 × 2√3/3 ≈ √2d/2 × 0.9045085
Area of external face of S module (in equilateral triangles) = BA × h’
= a√(7-3√5) × a√2/2φ ≈ a² × 0.2063310 ≈ d × (√2d/2 × 0.9045085)
90° height of S module = AD
60° height of S module = h” = AD × √6/2
Volume of S module (in tetrahedra) = Area of external face × h”

The volume of the A quanta module is 1/24th that of the unit tetrahedron, or ≈ 0.041666, and the volume of the S quanta module is about 1.87415 times that of the A quanta module. Fuller thought the S module’s volume was 1.0820 times that of the A module’s. If we divide the volume of the S quanta module by 2, the volume of the A quanta module is about 1.06715 times that of the halved S quanta module, and that’s as close as I’ve come to Fuller’s figure, which remains a mystery.

The volume of space in the octahedron that is not occupied by the icosahedron is the S module’s volume times 24 ≈ 1.874147087. That leaves a volume of approximately 2.125852913 for the inscribed icosahedron. I haven’t found anything meaningful in these numbers.