Pyritohedron Dimensions and Whole-Number Volume

Greg Frederick

Note: For instructions on how to construct the Weaire-Phelan structure, see my post: Construction Method for the Pyritohedron and Tetrakaidecahedron of the Weaire-Phelan Structure.

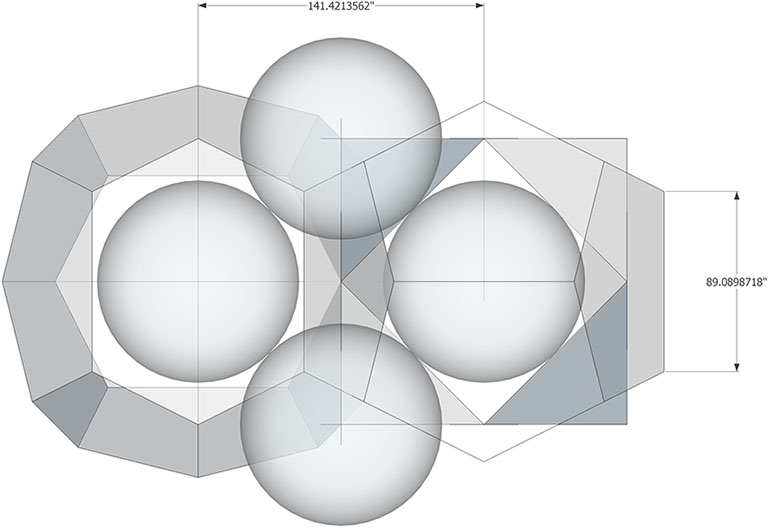
Pyritohedra and tetrakaidecahedra close pack to constitute the Weaire-Phelan structure (or Weaire-Phelan “matrix” as I prefer to call it, and, when dimensioned appropriately, align precisely with the distribution of nuclei in the isotropic vector matrix. The unit vector (d in the illustration below) is identical with the unit vector (sphere diameter) of the isotropic vector matrix.

The Weaire-Phelan structure: the tetrakaidecahedron with height of tall pentagonal face (d) and the pyritohedron in with base of pentagonal face (a) in relation to the distribution of unique (red) and non-unique (pink) nuclei of the isotropic vector matrix.
The pyritohedron (right) and the tetrakaidecahedron (left) combine to form the Weaire-Phelan structure (or matrix) and, when dimensioned appropriately, align with the distribution of unique nuclei (red) and shared nuclei (pink) in the isotropic vector matrix.

The pyritohedron and, presumably, the tetrakaidecahedron have identical rational volumes in both cubic and tetrahedral units of measure. For the cubic volume, we take the long edge of the pentagonal face as the unit length (a in the illustrations). For the tetrahedral volume, we take the diameter of the sphere as the unit length (d in the illustrations).

The pentagonal face of the pyritohedon with the angles and dimensions necessary for calculating its area.
The dimensions of the pyritohedron’s pentagonal face are all related rationally to the length of its long edge, a, which is irrational with respect to d, the diameter of the unit sphere.

When we measure the angles, edge lengths, and radii of the pyritohedron, the numbers do not inspire confidence. It would seem unlikely that so many irrational numbers could possibly result in a rational, whole-number volume. But they do.

a = long edge or base of pentagonal face
d = diameter of sphere*
d = a × ³√4 × √2/2
a = d × ³(√2/2) = (d√2)/(³√4) = d√2 × ³√(1/4)

*d is identical with the unit vector of the isotropic vector matrix. In the Weaire-Phelan matrix, it aligns with the height vectors connecting the base with the peak of the smaller of the two pentagonal faces of the tetrakaidecahedron, and to the radial vectors connecting the height vector’s endpoints (see illustration below).

Lines connecting the center of the tetrakaidecahedron with the base and peak of its tall pentagonal faces are equal to the diameter of the nuclei distributed as pyritohedra in the Weaire-Phelan Matrix.
The unit vector, d, used in the volume calculations of the pyritohedron (right) is identical with the unit vector in the isotropic vector matrix, i.e. the diameter of the unit sphere. It aligns with the Weaire-Phelan matrix as the radial vectors and face heights in the tetrakaidecahedron (left).

The long edge of the pyritohedron’s pentagonal face, a, (which, when taken as unit length results in a cubic volume for the pyritohedron of 4a³) seems to be related to the diameter of the sphere, d, by ³(√2/2) or about 0.890898718. I don’t have a geometric proof to account for the appearance of this third root, but the number seems to work to at least 7 decimal places in my computer models, and the irrational roots cancel out perfectly in the volume calculations to produce the rational result of 24d³ for the tetrahedral volume.

Pyritohedron specifications:

  • 12 irregular pentagonal faces, 20 vertices, 30 edges
  • Face angles:
    • atan(2√5) + atan(√5/4) ≈ 106.6015496°
    • atan(√5/10)+90° ≈ 102.6043826°
    • 2atan(4√5/5) ≈ 121.588136°
  • Dihedral angle: 2atan(2) ≈ 126.8698976°
  • Volume (in tetrahedra): 24a³√2
  • Volume (in tetrahedra): 24d³
  • Cubic volume: 4a³
  • Cubic volume: 2d³√2
  • Quanta modules: 576 modules, types unknown*
  • Surface area (in equilateral triangles): 8a²√15
  • Surface area (in squares): 6a²√5
  • In-sphere radius: 2a/√5
  • Mid-sphere radius (center to mid-long-edge): a
  • Circum-sphere radius: a√5/2

*It should be possible to construct the pyritohedron from quanta modules, but may involve one or more variants of those quanta modules already described by by Fuller.

The image below shows my computer model with the calculated dimensions accurate to 7 decimal places.

Illustration showing key dimensions (accurate to 7 decimal places) of the Weaire-Phelan matrix sized to the unit spheres of the isotropic vector matrix.
If the circumsphere radius of the tetrakaidecahedron is of unit length (one sphere diameter), the long edge of the pyritohedron is, to an accuracy of at least seven decimal places, equal to √2׳√(1/4), or about 0.890898718, which produces a rational volume of 24 unit tetrahedra for both the pyritohedron and its complementary tetrakaidecahedron.

Leave a comment