All … regular, omnisymmetric, uniform-edged, -angled, and -faceted, as well as several semisymmetric, and all other asymmetric polyhedra other than the icosahedron and the pentagonal dodecahedron, are described repetitiously by compounding rational fraction elements of the tetrahedron and octahedron. These elements are known in synergetics as the A and B Quanta Modules.
—R. Buckminster Fuller, Synergetics, Section 910.11
The pentagonal dodecahedron (or “regular dodecahedron in conventional geometry) is the double of the regular icosahedron; the 12 vertices of the regular icosahedron can be truncated to form the 12 faces of the pentagonal dodecahedron, and the 20 vertices of the pentagonal dodecahedron can be truncated to form the 20 faces of the regular icosahedron. (See: Icosahedron.)
But I think a more interesting symmetry is with the counterpart to the regular icosahedron that occurs in the jitterbug transformation of the isotropic vector matrix (see Icosahedron Phases of the Jitterbug). The counterpart to the regular icosahedron can be constructed from the pentagonal dodecahedron by truncating 8 of its 20 vertices along triangles formed by joining the vertex’s three face diagonals.
Otherwise, the pentagonal dodecahedron does not appear in Fuller’s geometry. Like the icosahedron, it is incommensurate with the isotropic vector matrix and its volume is irrational whether measured in cubes or in tetrahedra.
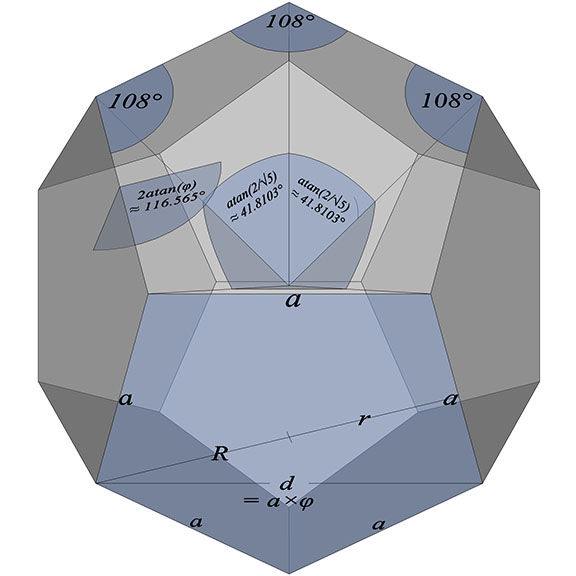
The pentagonal, or “regular,” dodecahedron with edge length, a, has the following dimensions when expressed in terms of the golden ratio (φ):
- φ = golden ratio, (√5+1)/2
- a = edge length = d/φ = d(φ-1)
- d = diagonal = a×φ
- 12 pentagonal faces, 20 vertices, 30 edges
- Face angles all 108°
- Dihedral angle: 2atan(φ) ≈ 116.565051°
- Central angle: atan(2/√5) ≈ 42.8103°
- r = in-radius (unit edge length, a): a×φ/2√(3-φ)
- r = In-radius (unit diagonal, d): d×1/(2√(3-φ))
- R = Circum-radius (unit edge length, a): a/√(3-φ)
- R = Circum-radius (unit diagonal, d): d/√(φ+2)
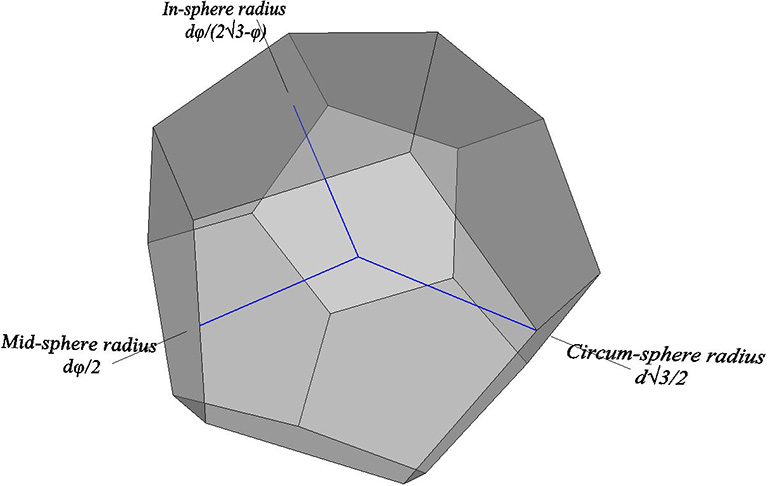
- Ri = Insphere radius (unit edge length (a): a×(φ+1)/√(2(5-√5)) –or– a×φ²/2√(3-φ)
- Ri = Insphere radius (unit diagonal d): d×φ/√(2(5-√5) –or– d×φ/2√(3-φ)
- Rm = Midsphere radius (unit edge length a): a×(φ+1)/2
- Rm = Midsphere radius (unit diagonal d): d×φ/2
- Rc = Circumsphere radius (unit edge length a): a×φ√3/2
- Rc = Circumsphere radius (unit diagonal d): d×√3/2
- Volume (cubic, unit edge length (a): a³×5φ³/(5-√5)
- Volume (tetrahedral, unit edge length (a): a³×φ³×30√2/(5-√5)
- Volume (cubic, unit diagonal (d): d³×(φ+2)/2
- Volume (tetrahedral, unit diagonal (d): d³×3√2(φ+2)
- Quanta modules: n/a
The volume of the pentagonal dodecahedron seems to be irrational regardless of which of its dimensions is taken as unity, and regardless of whether the volume is calculated in cubes or tetrahedra, as shown in the following table:
| unit dimension | formula (cubic volume × 6√2) | volume (tetrahedra) |
|---|---|---|
| edge length (a) | a³ × 5φ³/(5-√5) × 6√2 | ≈65.02372058516 |
| diagonal (d) | d³ × (φ+2)/2 × 6√2 | ≈15.35001820805 |
| in-radius (r) | r³ × 20φ√(7-4φ) × 6√2 | ≈199.50093013318 |
| circum-radius (R) | R³ × 5φ³√(3-φ)/2 × 6√2 | ≈105.63743770232 |
| insphere radius (Ri) | Ri³ × 20√(7-4φ)/φ² × 6√2 | ≈47.09578108587 |
| midsphere radius (Rm) | Rm³ × 40/(φ³(5-√5)) × 6√2 | ≈22.14576445397 |
| circumsphere radius (Rc) | Rc³ × (20√3)/(9(3-φ)) × 6√2 | ≈23.63289905196 |