“… we observe the child taking the “me” ball and running around in space. There is nothing else of which to be aware; ergo, he is as yet unborn. Suddenly one “otherness” ball appears. Life begins. The two balls are mass-interattracted; they roll around on each other. A third ball appears and is mass-attracted; it rolls into the valley of the first two to form a triangle in which the three balls may involute-evolute. A fourth ball appears and is also mass-attracted; it rolls into the “nest” of the triangular group. . . and this stops all motion as the four balls become a self-stabilized system: the tetrahedron.“
—R. Buckminster Fuller, Synergetics, 100.331

“The mathematics involved in synergetics consists of topology combined with vectorial geometry. Synergetics derives from experientially invoked mathematics. Experientially invoked mathematics shows how we may measure and coordinate omnirationally, energetically, arithmetically, geometrically, chemically, volumetrically, crystallographically, vectorially, topologically, and energy-quantum-wise in terms of the tetrahedron.”
—ibid., 201.01

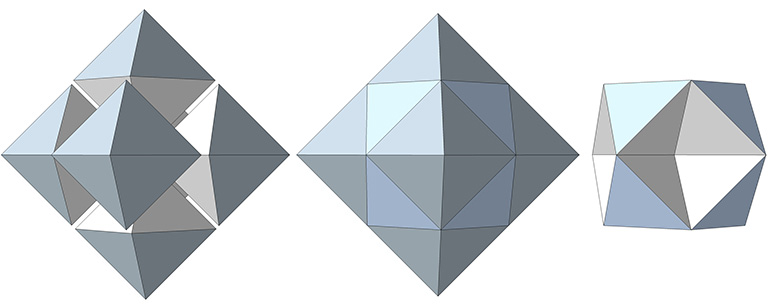
Nature’s simplest structural system is the tetrahedron. Regular tetrahedra, however, do not combine to fill all-space (as do cubes, for example). In order to fill all-space, the regular tetrahedron must be complemented by the regular octahedron. Together they produce what Fuller conceived as the simplest, most powerful structural matrix in the universe, the octahedron-tetrahedron matrix, which he was able to patent in 1961 and subsequently copyright under the trademark name, the “octet truss.”

This complementary relationship between the tetrahedron and its space-filling counterpart, the octahedron, is demonstrated by stacking four tetrahedra vertex-to-vertex to create a larger tetrahedron. In doing so, we discover that we have inadvertently produced an octahedron at its center.

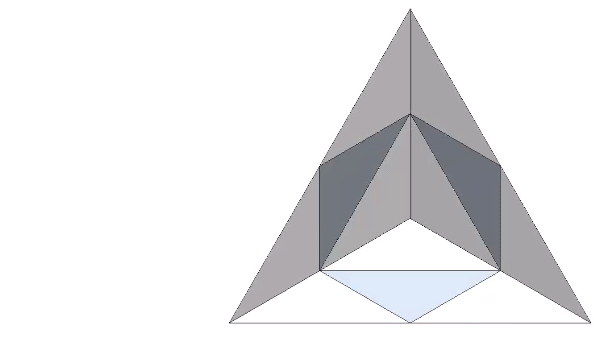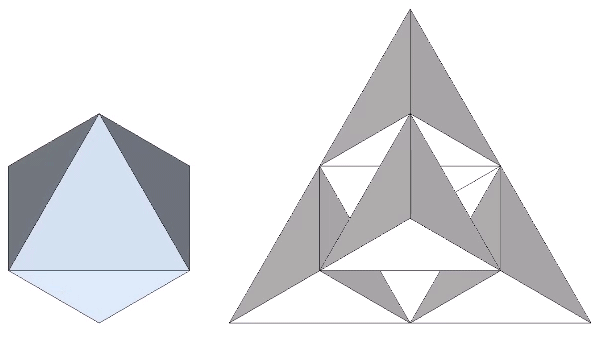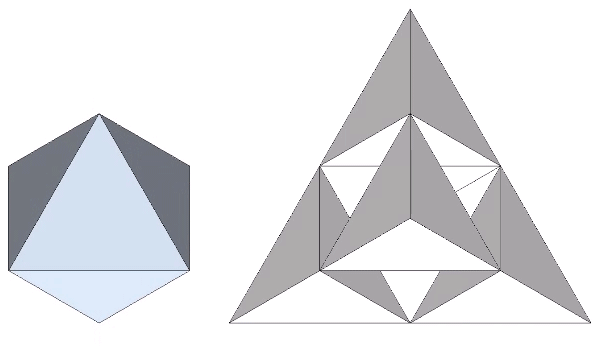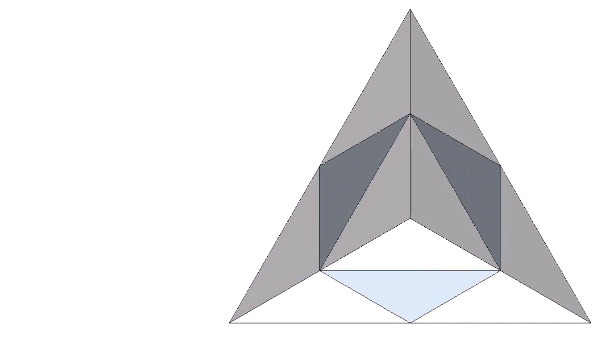
Fuller considered this system of all-space-filling tetrahedra and octahedra to be nature’s own coordinate system: the isotropic vector matrix.

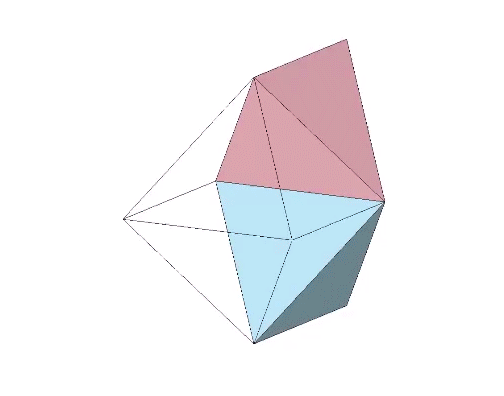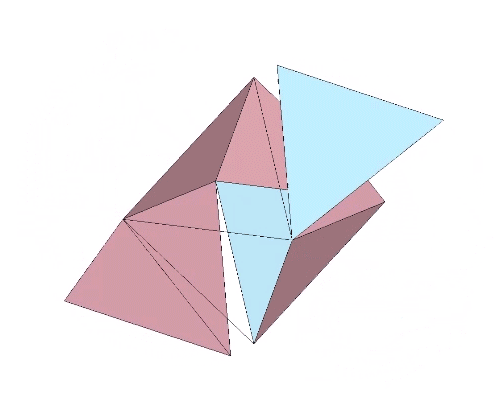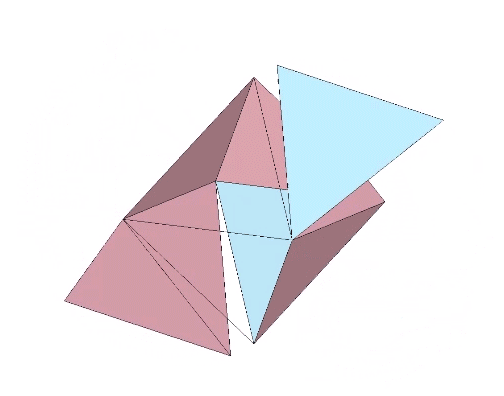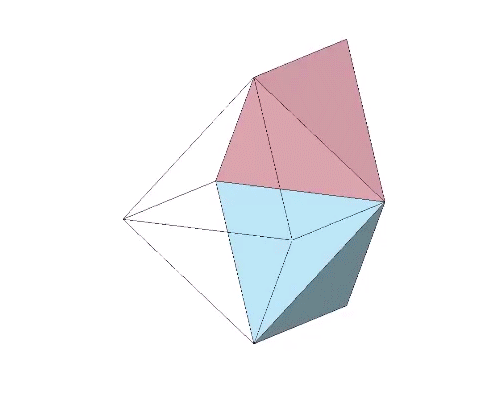
The regular tetrahedron is perhaps most easily conceived on the orthogonal grid as two unit length edges separated by a distance of √2/2 and oriented at 90° to the other (thick red lines in the figure below). Connecting their endpoints forms the the regular tetrahedron of edge length, a.

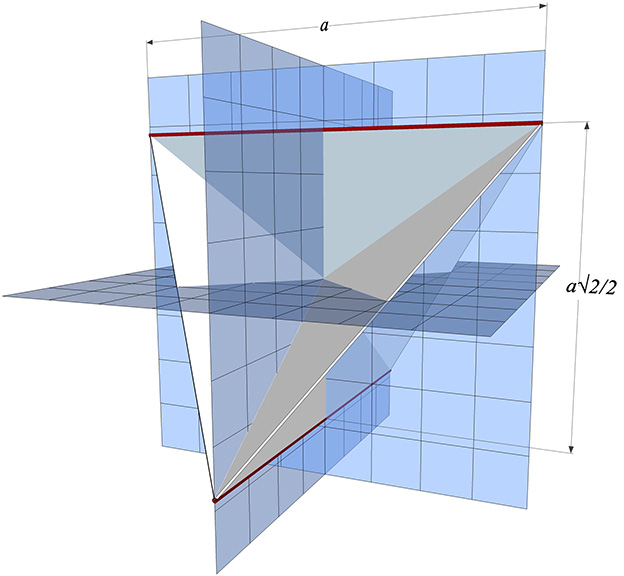
The Regular Tetrahedron

a = edge length

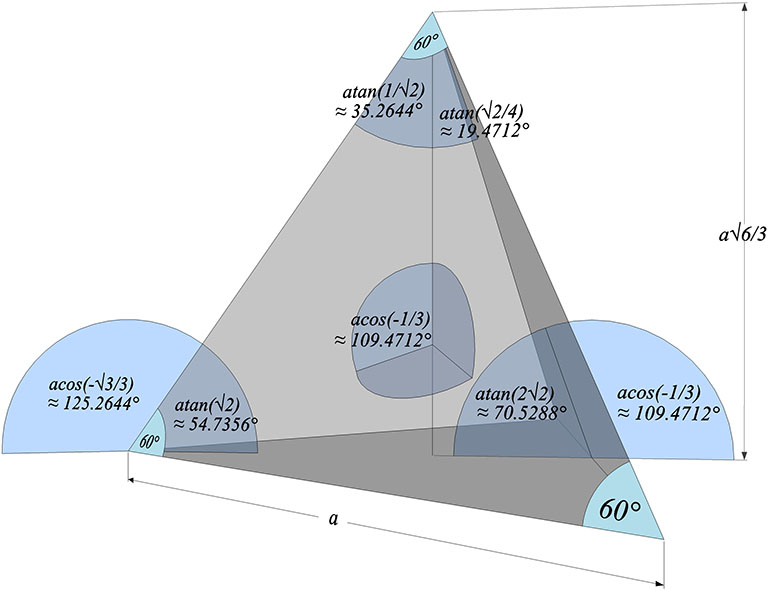
• 4 equilateral triangle faces, 4 vertices, 6 edges
• Face angles all 60°
• Central angles all arccos(-1/3) ≈ 109.4712°
• Dihedral angle: atan(2√2) ≈ 70.5288°
• Volume (in tetrahedra): a³
• Cubic Volume: a³√2/12
• A Quanta Modules: 24
• B Quanta Modules: 0
• Surface area (in equilateral triangles): 4a²
• Surface area (in squares) 4a²√3/4
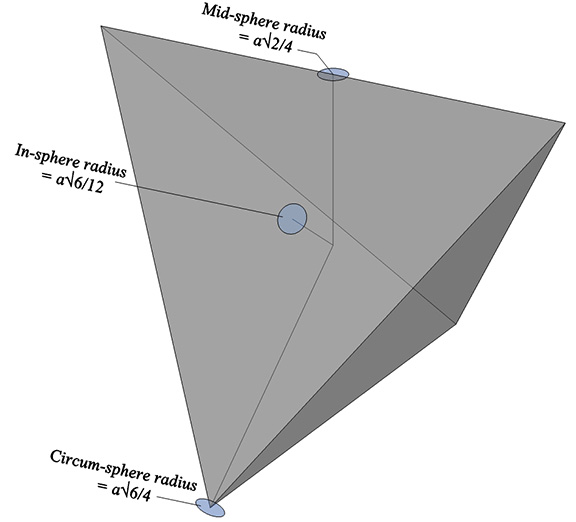
• In-sphere radius (center to mid-face): a√6/12
• Mid-sphere radius (center to mid-edge): a√2/4
• Circumsphere radius (center to vertex): a√6/4

The surface, central, dihedral and other angles of the regular tetrahedron:

The in-sphere radius (center to mid-face), mid-sphere radius (center to mid-edge), and circumsphere radius (center to vertex) of the regular tetrahedron:

The regular tetrahedron has three natural poles, or axes, of spin, the three axes running between mid-edges.

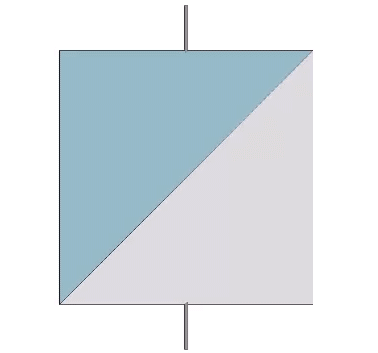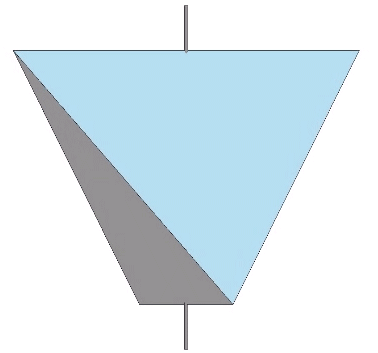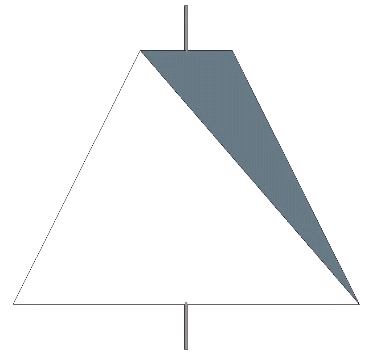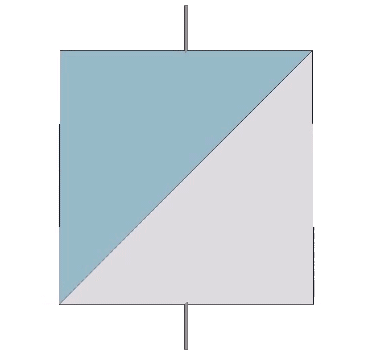
The A quanta module is derived from the regular tetrahedron. Through symmetrical quartering and bisecting the regular tetrahedron is divided into 24 A quanta modules, 12 positive and 12 negative.

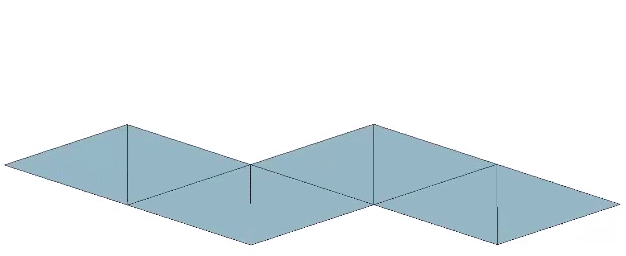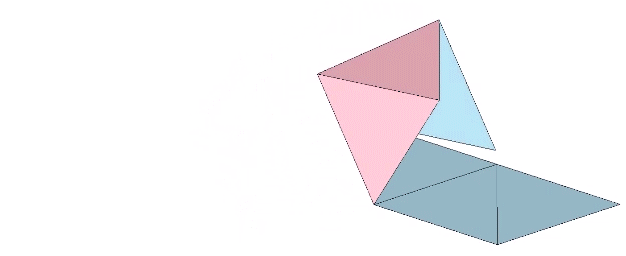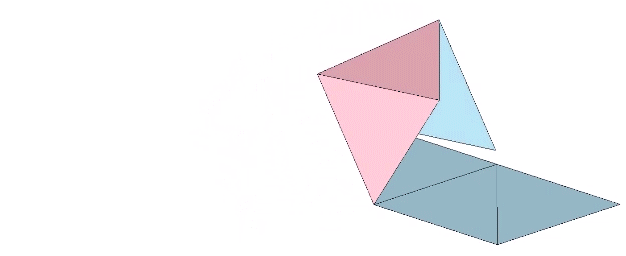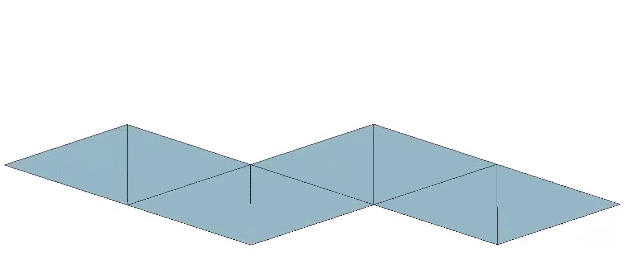
The regular tetrahedron can be constructed from a paper strip with three consecutive folds of arccos(-1/3), approximately 109.4712°.

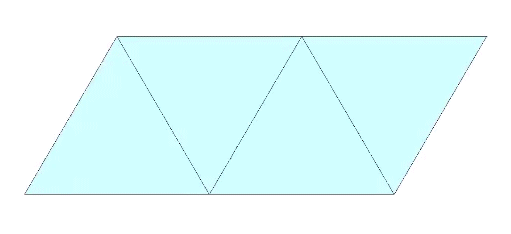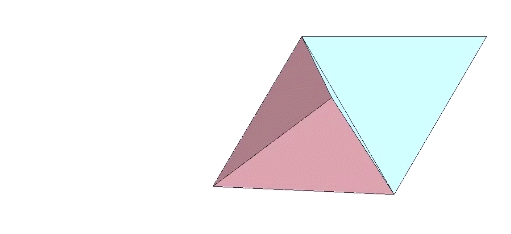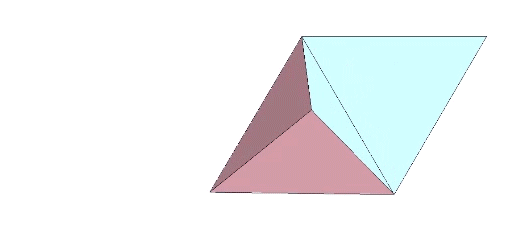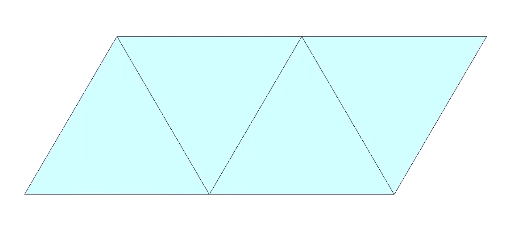
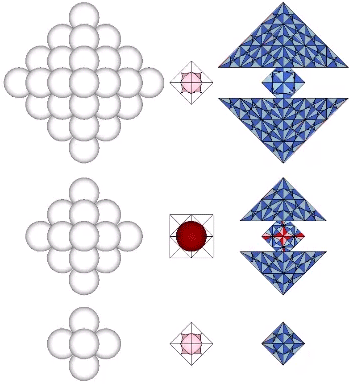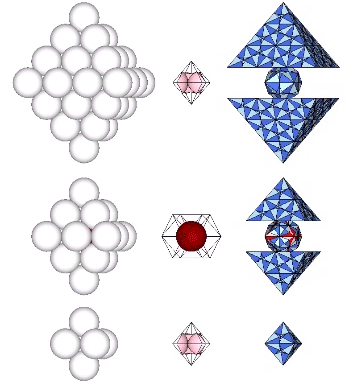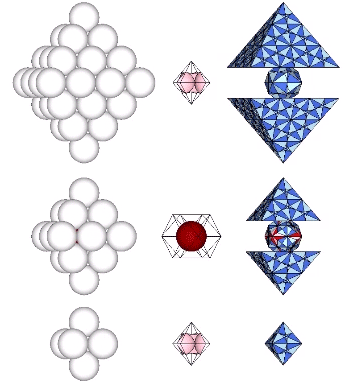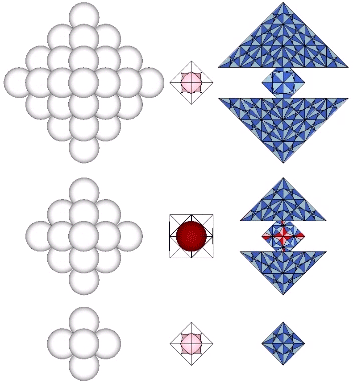
Spheres close pack as tetrahedra in even-numbered layers around octahedra (spaces) and VEs (spheres). In odd-numbered layers, the spheres surround a positive or negative tetrahedron (concave octahedron interstice). The growth pattern repeats every fourth layer, with the first layer surrounding a positive tetrahedron (concave octahedron interstice); the second layer surrounding an octahedron (concave VE space); the third layer surrounding a negative tetrahedron (concave octahedron interstice); and the fourth layer surrounding a VE (sphere).

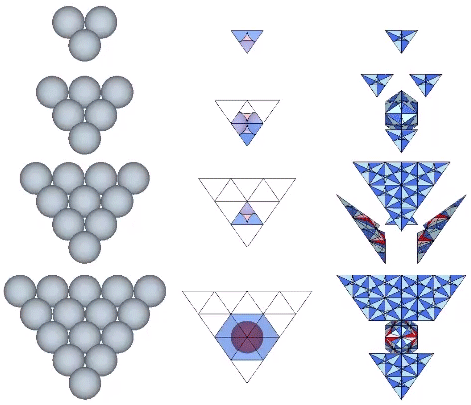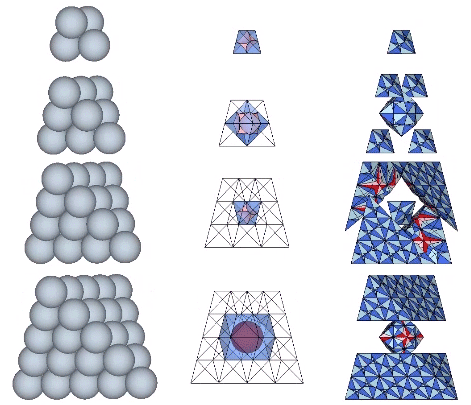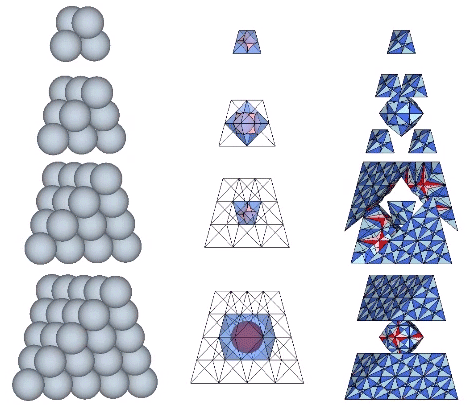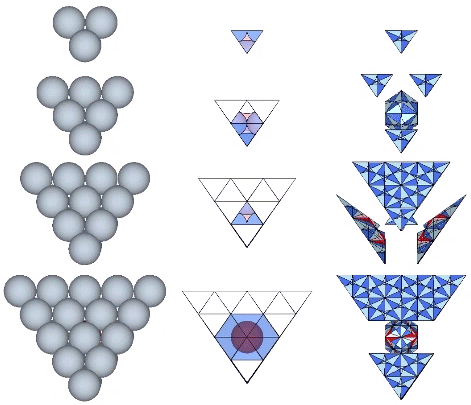
Number of spheres in outer layer: 2F²+2
F = edge frequency, i.e., number of subdivisions per edge

Total number of spheres: [(N+1)³-(N+1)]/6
N = number of spheres per edge

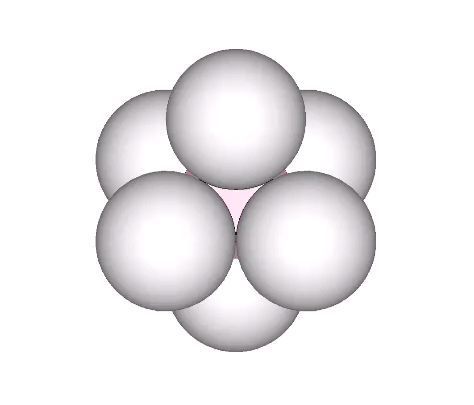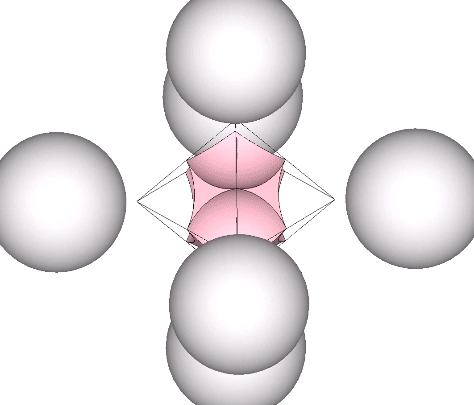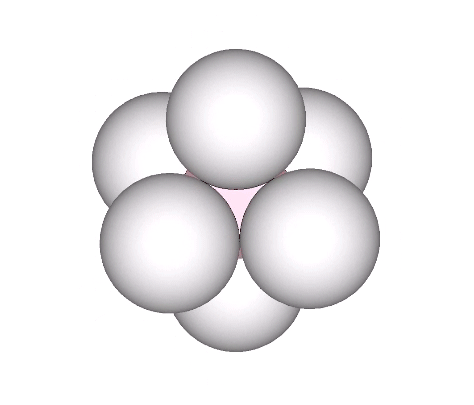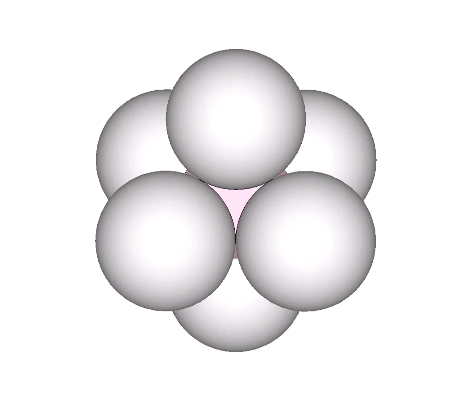
A single sphere is free to rotate in any direction. Two tangent spheres are free to rotate in any direction but must do so cooperatively. Three spheres can rotate cooperatively about a single axis, i.e., they may involute and evolute along an axis perpendicular to the line connecting them with the center of the group. The addition of a fourth sphere acts as a lock, preventing all from rotating independently of the others. No rotation is possible, making the minimum stable closest-packed-sphere system: the tetrahedron.

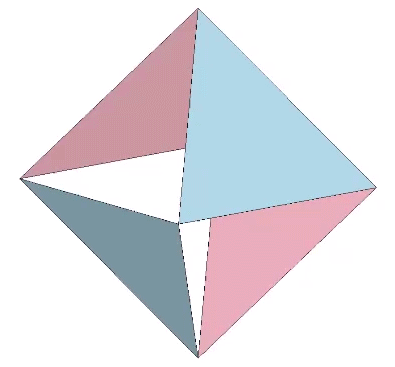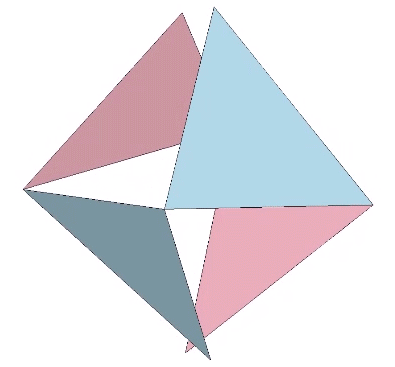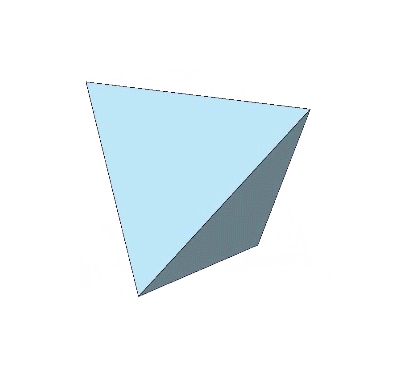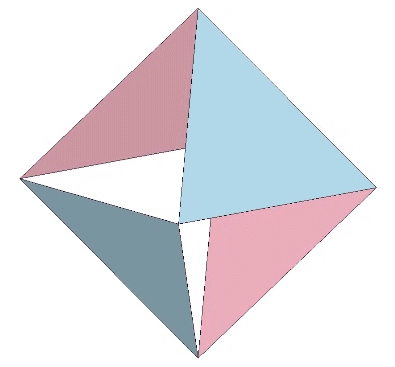
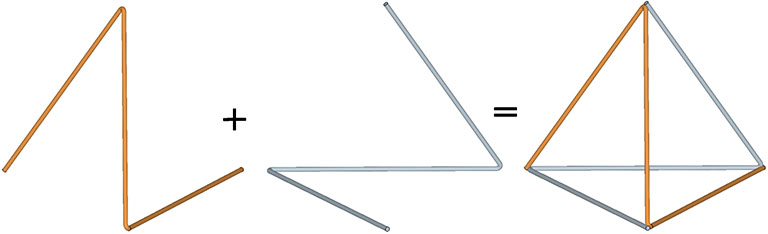
Two triangular helical units combine to form one 4-sided tetrahedron. 1+1 = 4. Fuller would use this as a primary example of synergy and complementation. The two additional triangles were always there but invisible until the first two were combined into a system.

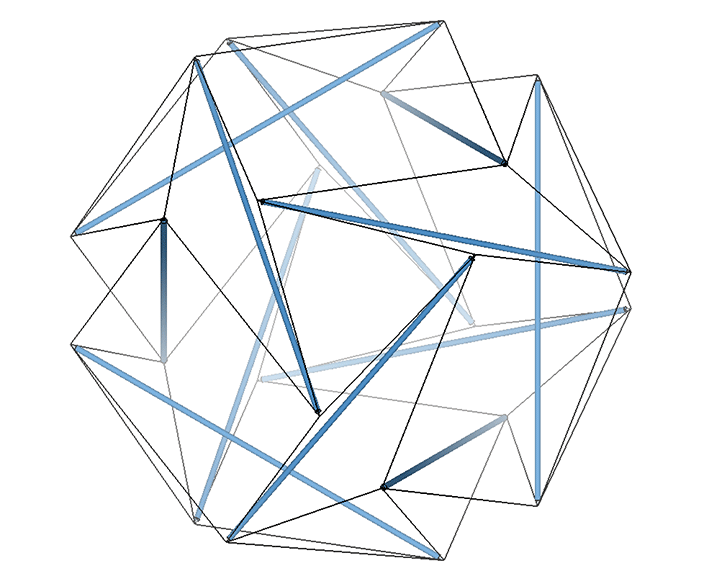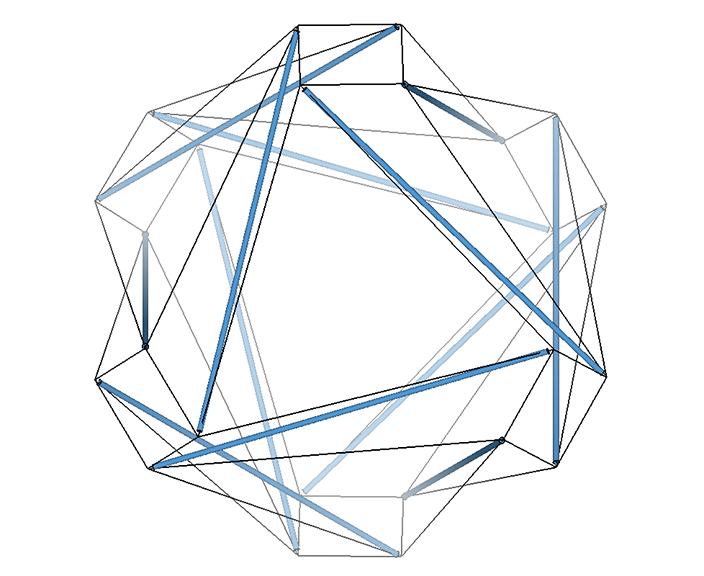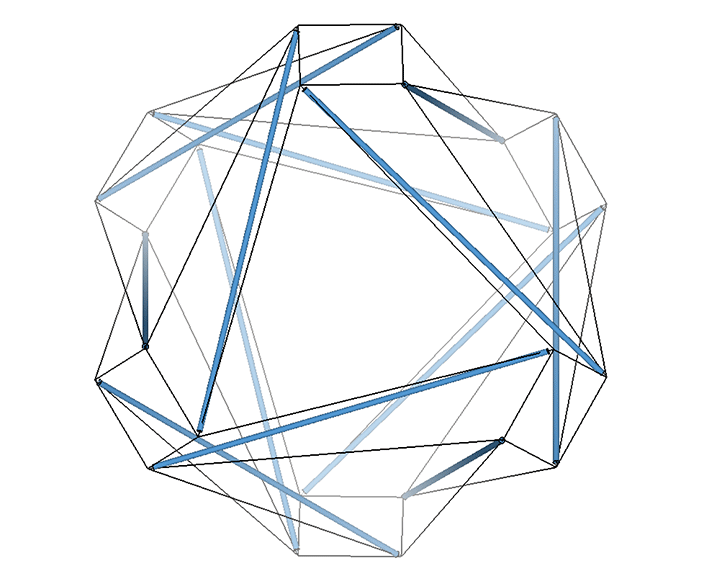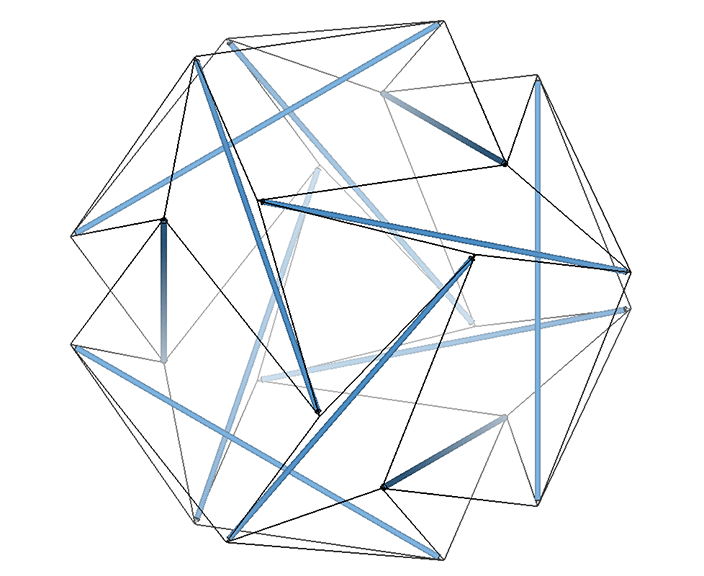
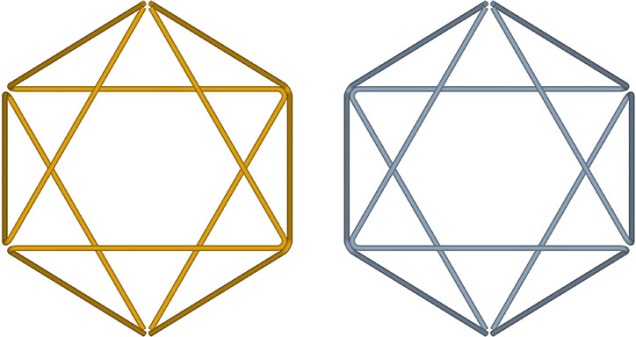
The tetrahedron in its tensor-equilibrium phase has the overall shape of the Jessen orthogonal icosahedron. This 6-strut tensegrity is uniquely ambidextrous, i.e., neither right- nor left-handed; the vertex loops may be pulled inward to generate either a positive or a negative tetrahedron.

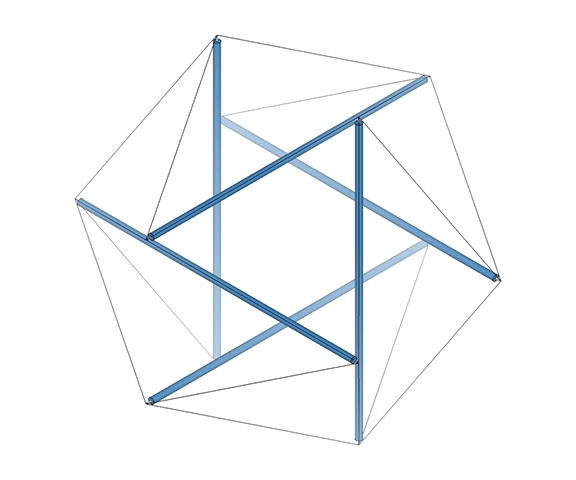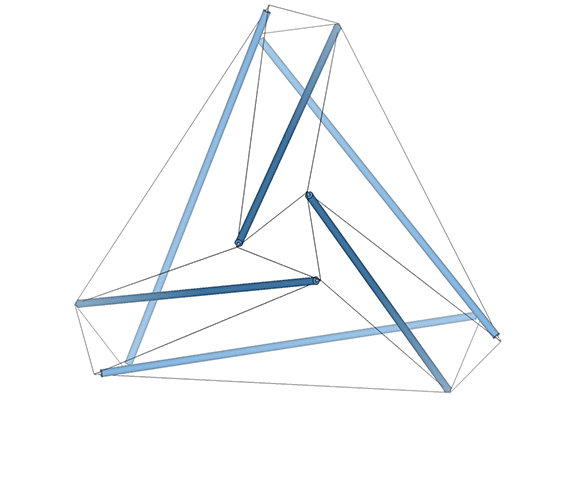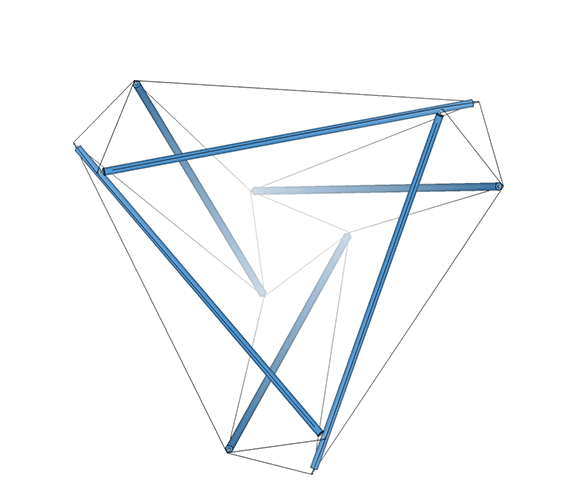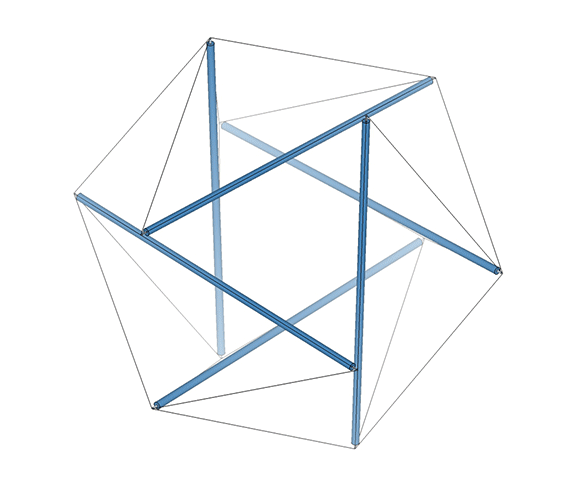
In the interstitial model of the isotropic vector matrix, the interstices occupy the positions defined by tetrahedra in the vector model, and by cubes in the quanta model. The interstices, i.e. the space between spheres close-packed as tetrahedra, describe a concave octahedron. (See Spheres and Spaces.)

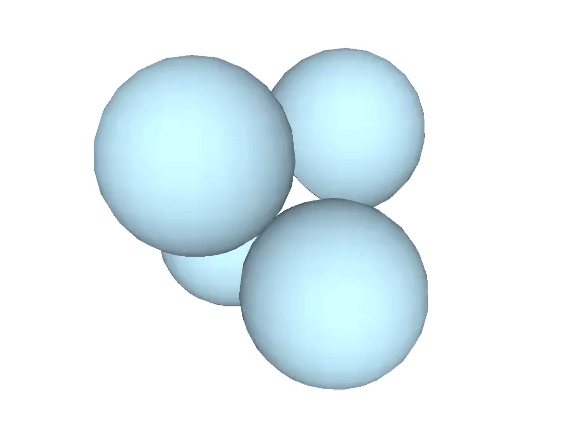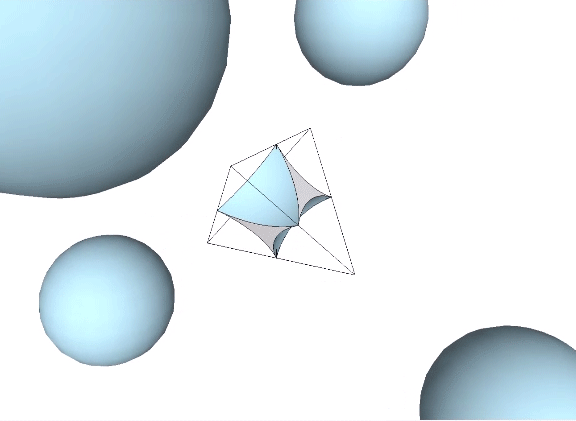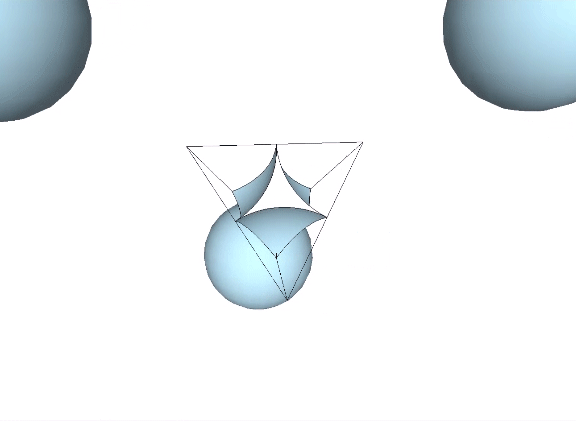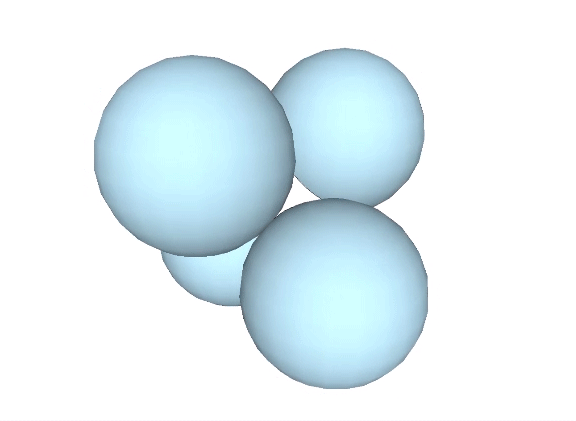
This concave octahedron and its enclosing tetrahedron retain their shape and position throughout the jitterbug transformation. Only their orientation changes, with the tetrahedron rotating 90° between phases. See: The Jitterbug.

In any omni-triangulated structural system, that is, for any polyhedron structurally stabilized through triangulation:

1. the number of vertices (“crossings” or “points”) is always evenly divisible by two;
2. the number of faces (“areas” or “openings”) is always evenly divisible by four, and;
3. the number of edges (“lines,” “vectors,” or “trajectories”) is always evenly divisible by six.

This holds true for any polyhedron of whatever its size or complexity, just so long as its faces (areas, openings) are all triangulated and therefore constitute a “structure” by Fuller’s definition, i.e. any system that holds its shape without external support. The point here is that the same numbers, two, four, and six, fundamentally describe the tetrahedron:

1. The number of (non-polar) vertices in a tetrahedron is two;
2. The number of faces (“areas” or “openings”) in a tetrahedron is four, and;
3. The number of edges (“lines”, “vectors”, or “trajectories”) in a tetrahedron is six.

The tetrahedron is the minimum structural system and therefore the prime unit of volumetric measurement in Fuller’s geometry. The regular tetrahedron, unit-diagonal cube, octahedron, vector equiilbrium (VE), rhombic dodecahedron, and other polyhedra, both regular and irregular, all have rational, whole number volumes when measured in tetrahedra. See also: Polyhedra With Whole Number Volumes; Areas and Volumes in Triangles and Tetrahedra, and Calculating Volumes of Regular Polyhedra.

“When four tetrahedra of a given size are symmetrically intercombined by single bonding, each tetrahedron will have one of its four vertexes uncombined, and three combined with the six mutually combined vertexes symmetrically embracing to define an octahedron; while the four noncombined vertexes of the tetrahedra will define a tetrahedron twice the edge length of the four tetrahedra of given size; wherefore the resulting central space of the double-size tetrahedron is an octahedron. Together, these polyhedra comprise a common octahedron-tetrahedron system.”
—R. Buckminster Fuller, Synergetics, 422.03

Nature’s simplest structural system is the tetrahedron. Regular tetrahedra, however, do not combine to fill all-space (as do cubes, for example). In order to fill all-space, the regular tetrahedron must be complemented by the regular octahedron. Together they produce what Fuller conceived as the simplest, most powerful structural system in the universe, the octahedron-tetrahedron system, which he was able to patent in 1961 and subsequently copyright under the trademark name, the “octet truss.”

If we stack six octahedra edge-to-edge to create a larger octahedron we discover that we have inadvertently produced eight tetrahedra at its center. The eight edge-bonded tetrahedra share a common vertex and form the vector equilibrium (VE).

Another name for this system of all-space-filling tetrahedra and octahedra is the isotropic vector matrix.

One of the simplest ways to construct the octahedron is to orient three squares to the three planes of the Cartesian grid, centered on the origin and turned so that each of their vertices lie on the axes.

The Regular Octahedron

a = edge length

• 8 equilateral triangle faces, 6 vertices, 12 edges
• Face angles all 60°
• Dihedral angle: acos(-1/3) ≈ 109.4712°
• Central angles: all 90°
• Volume (in tetrahedra): 4a³
• Cubic volume: a³×√2/3
• A quanta modules: 48
• B quanta modules: 48
• Total quanta modules: 96
• Surface area (in equilateral triangles): 6a²
• Surface area (in squares): 6√3a²/4
• In-sphere radius: a√6/6
• Mid-sphere radius: a/2
• Circum-sphere radius: a√2/2

The surface, central, dihedral, and other interior and exterior angles of the regular octahedron.

The in-sphere (center to mid-face), mid-sphere (center to mid-edge), and circumsphere (center to vertex) radii of the octahedron.

The regular octahedron consists of 96 quanta modules, evenly distributed between A and B modules with 48 each.

The regular octahedron can be constructed from a single paper strip along seven consecutive folds of atan(2√2), or approximately 70.5288°, each. See also: Polyhedra From Polygonal Strips.

The octahedron may be produced through the unfolding of one positive and one negative tetrahedron.

The octahedron can also be produced from one positive or one negative tetrahedron alone. This produces an octahedron of four triangular facets and four empty triangular windows. This can be demonstrated through a kind of jitterbug transformation, as shown in the figure below.

Spheres close-pack as octahedra around a central sphere or nucleus in even numbered layers only. The odd numbered layers surround a space, or concave vector equilibrium (VE).

Number of spheres in outer shell: 4F²+2
F = edge frequency, i.e., the number of subdivisions per edge

Total number of spheres: (4N³+2N)/6
N = number of spheres per edge

The tensor equilibrium phase of the octahedron suggests the overall shape of the VE, with its six vertex loops forming the square “faces” of the VE. As with all polyhedra, with the exception of the tetrahedron (see: The Dual Nature of the Tetrahedron), the vertex loops are oriented in either a clockwise or a counter-clockwise direction, and when pulled in tight form the six vertices of either the positive or the negative octahedron. (See also: Tensegrity.)

In the interstitial model of the isotropic vector matrix, the spaces between spheres occupy the positions defined by the octahedra in the vector model, and by one of the two rhombic dodecahedra in the quanta model. The spaces, i.e., the space between spheres close-packed as octahedra, describe a concave VE.

In the jitterbug transformation, the concave vector equilibria (VE’s) and their enclosing octahedra transform into spheres, and vice-versa. See: Spheres and Spaces; Spaces and Spheres (Redux), and; The Jitterbug.

All the structural (i.e. triangulated) polyhedra may be constructed from an even number triangular helices, or what Fuller called one half of a structural quantum. The tetrahedron and icosahedron require an equal number of clockwise and counter-clockwise helices. However, the octahedron is curiously constructed from an even number of clockwise, or an even number of counter-clockwise triangular helices, which seems to contradict our intuitive concept of structure as a knot of positive and negative forces.

This underscores, I think, our understanding of the octahedron as the space between the spheres, and the void between the tetrahedra, of the isotropic vector matrix.

Note further that the endpoints of the helices converge on just two of the octahedron’s six vertices, resulting in a preferred axis of spin, and of wave propagation (see Isotropic Vector Matrix as Transverse Waves.)