The golden ratio appears nowhere in Fuller’s two-volume exposition of his geometry, Synergetics. This isn’t surprising; Fuller eschewed irrational numbers, and his mathematical explorations persuaded him that all irrational numbers, like the golden ratio, could be expunged from our science if only we adopted his physical geometry, grounded in the real and experimentally verifiable rather than the axiomatic. But the golden ratio turns up again and again in both his and in conventional geometry, and recognizing it when you see it might lead to discoveries otherwise overlooked.
Expressed algebraically, the golden ratio (φ) is:
a+b/a = a/b = φ = (1+√5)/2 ≈ 1.618034
from which we can deduce the following selection of algebraic identities:
- φ² = φ + 1
- 1/φ = φ – 1
- 1/φ² = 2 – φ
- φ + φ² = φ³
- 1/φ – 1/φ² = 1/φ³
Expressed in trigonometry, the golden ratio has the following identities:
φ = 1 + 2sin(18°) -or- asin(1/2φ) = 18°
φ = 2cos(36°) -or- acos(φ/2) = 36°
φ = 2sin(54°) -or- asin(φ/2) = 54°
φ = 1/2cos(72°) -or- acos(1/2φ) = 72°
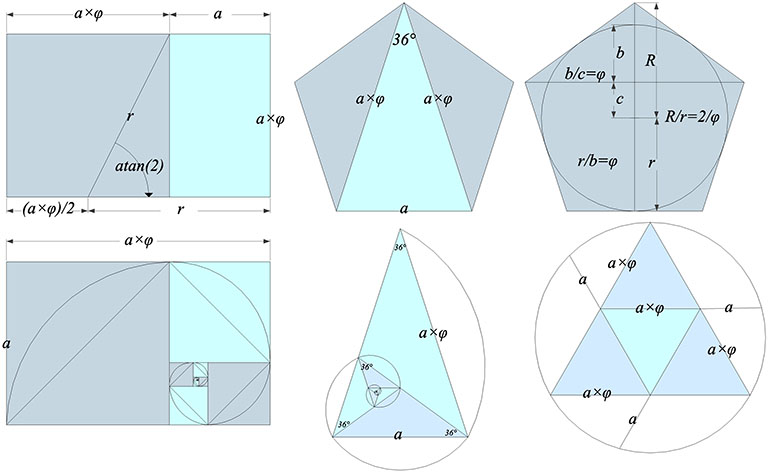
The visual geometric expressions of the golden ratio (φ) are numerous. Here is a selection in two dimensions:
The golden ratio turns up in many polyhedra, both regular and irregular.
Icosahedron
The icosahedron is perhaps the most famous example of the golden ratio in three dimensions. It can be constructed from three golden rectangles intersecting at 90° around a common center, as shown in the following illustration:

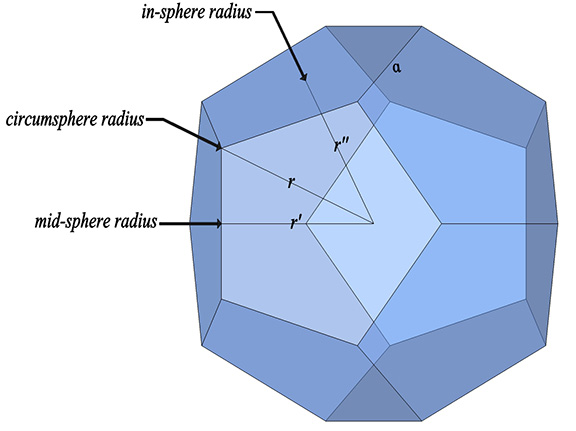
Regular (Pentagonal) Dodecahedron
Wherever pentagons are found, the golden ratio is sure to turn up. The in-sphere, mid-sphere and circumsphere radii of the pentagonal dodecahedron are all related to the golden ratio.
a = edge length
φ = (√5+1)/2
The in-sphere radius (center to mid-face) = a × φ²/2√(3-φ)
The mid-sphere radius (center to mid-edge) = a × φ²/2
The circumsphere radius (center to vertex) = a × √3φ/2
Rhombic Triacontahedron
The 30 faces of the the rhombic triacontahedron are identical with the golden rhombus.
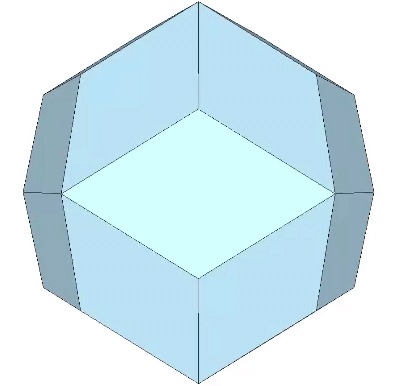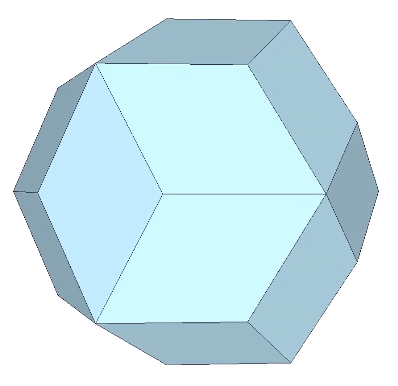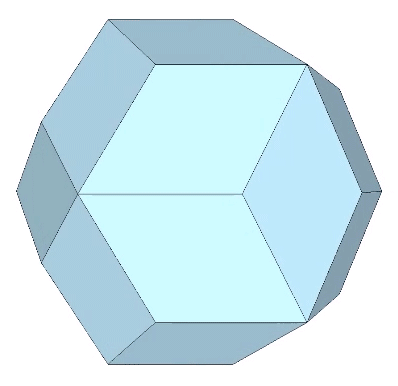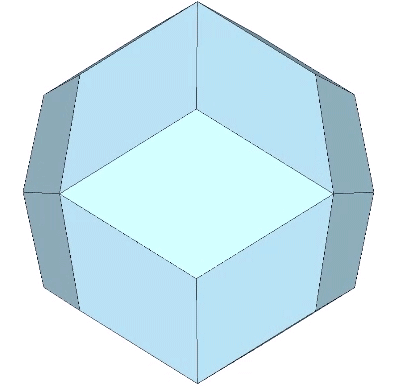
The long diagonal of the golden rhombus is φ times the length of its short diagonal.
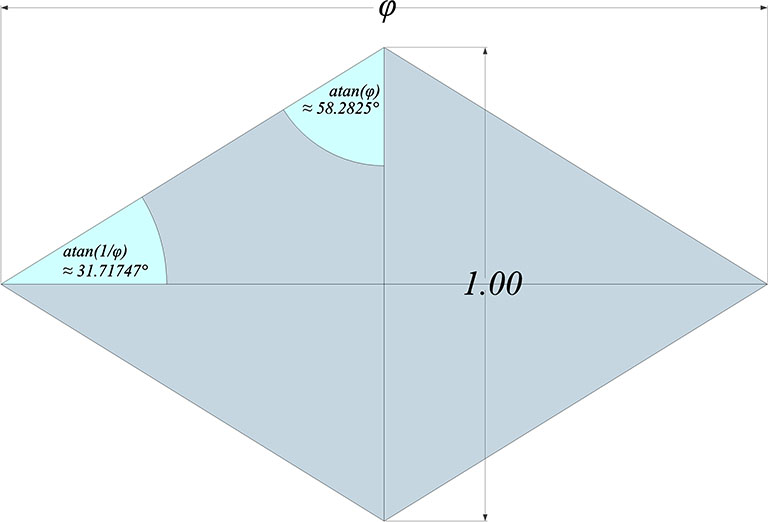
Its angles, atan(φ) (≈ 58.2825°) and atan(1/φ) (≈ 31.7175°) also turn up in the Basic Disequilibrium LCD Triangle.
Space-Filling Complement to the Regular Icosahedron
Twelve of the twenty faces of the space filling complement to the regular icosahedron are golden triangles. See: Icosahedron Phases of the Jitterbug.
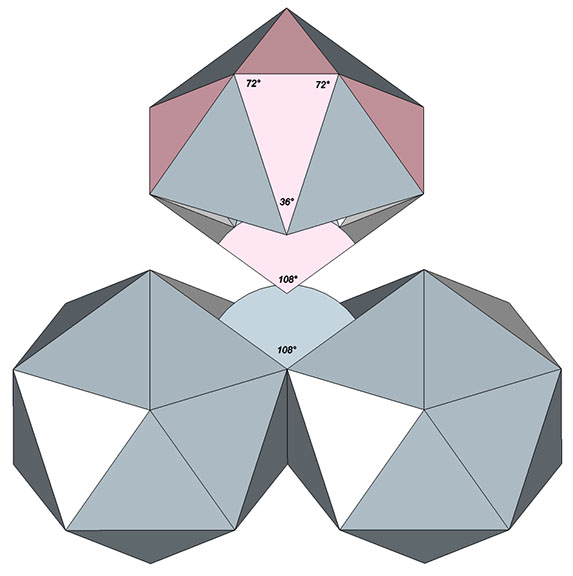
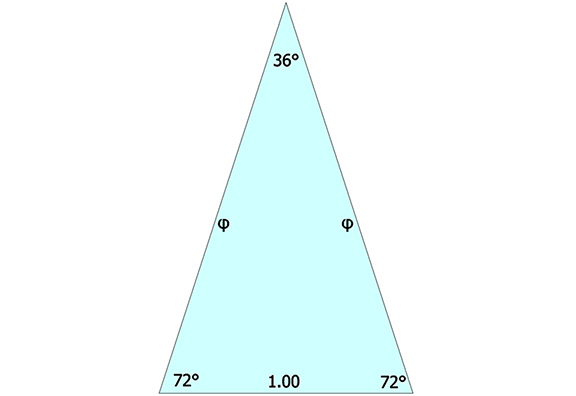
The golden triangle is an isosceles triangle in which the ratio of the sides to the base is φ, the golden ratio.