Calculating the Triangular Areas of Regular Polygons

Greg Frederick

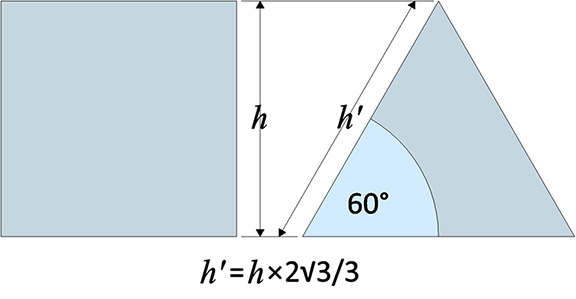
When calculating areas in equilateral triangles, the perpendiculars are measured at 30° from the vertical, or 60° from the horizontal. The equivalent 90° measures require a conversion factor of 2√3/3.

A square of height h measured at 90 degrees from the horizontal beside an equilateral triangle of height h' measured at 60 degrees from the horizontal. h' equals h times 2 times the square root of 3 divided by 3.

The area for any polygon, regular or irregular, may be calculated by dividing it into rhombuses and/or triangles, calculating the areas of each, and then summing the results.

The area of any regular, symmetrical polygon, may be calculated using its midradius (the distance from the center to mid-edge) and circumference.

Square area = 1/2 × midradius × circumference
Triangular area = 2√3/3 × midradius × circumference

The midradius is calculated from the circumradius, the distance from the center to any vertex.

midradius = circumradius × cos(180°/n), where n is the number of sides.

The following illustration shows the relationships between the number of sides, n, the circumradius, r, the midradius, r’, the edge length, a, and the angle 180°/n, Θ.

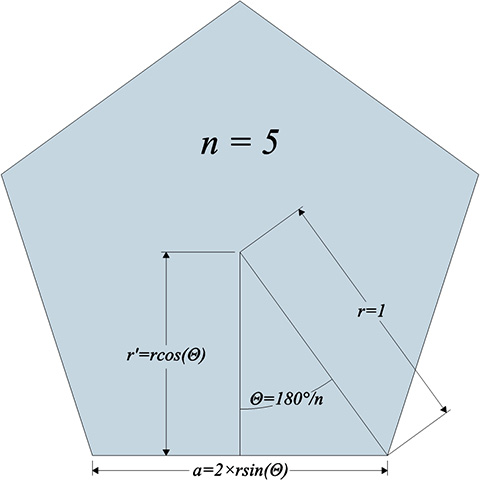
A pentagon with 5 equal sides. Theta is the angle which a line drawn from its center to mid-edge, r', makes with a line drawn from his center to one of the edge's vertices, r. If r equals 1, the edge length, a, equals 3 times r times the sine of theta.

With the above illustration in mind, the area formulas become:

Square area = n/2 × r cos(Θ) × 2r sin(Θ) = n×sin(2Θ)/2 × r²
Triangular area = n × (r cos(Θ) × 2√3/3) × 2×r sin(Θ) = n×sin(2Θ)/2 × 4r²√3/3

Note that as the number sides, n, approaches infinity, the expression, n×sin(Θ)/2, approaches pi (π). That is,

as (n→∞), (n×sin(360°/n)/2)→π

For more information, see Pi and the Synergetics Constants.

Examples

Hexagon (n=6; r=1.00)

Square area = (6r² sin(360°/6)/2) = 6r² √3/4 ≈ 2.598072×r²
Triangular area = 4r²√3/3 × (6 sin(360°/6)/2) = 4r²√3/3 × 6√3/4 = 6×r²

Circle (n=infinity; r=1.00)

Square area = r² (∞×sin(360°/∞)/2) = πr² ≈ 3.141593×r²
Triangular area = 4r²√3/3 × (∞×sin(360°/∞)/2) = πr²×4√3/3 ≈ 7.255197*×r²

* We might consider replacing pi (the ratio of the circumference of the circle to its diameter) with this number, the ratio of the circumference of the circle to the radius of its circumscribed hexagon. But then we might be likewise persuaded into replacing pi with the ratio of the circumference of the sphere to the radius of its circumscribed rhombic dodecahedron, which is a different number.

Leave a comment