Areas and Volumes in Triangles and Tetrahedra

Greg Frederick

Calculating areas and volumes in units of equilateral triangles and regular tetrahedra generally produces more rational results than calculating in units of squares and cubes. See Polyhedra With Whole Number Volumes.

The volume of a regular tetrahedron is conventionally calculated as the base times the perpendicular height divided by three. In the conventional Cartesian (90°) system of measurement, both the area of the triangular base and the volume of the tetrahedron are irrational numbers. Given an edge length of a, the height of the triangle is a√3/2, and the height of the tetrahedron is a√6/2. So,

Base of regular tetrahedron (in squares) = 1/2 × a × a√3/2, or a²√3/4, and
Volume of regular tetrahedron (in cubes) = 1/3 × a√3/2 × a√6/3, or a³√6/2

In Fuller’s 60° system of measurement, the area of the base triangle is simply a², and the volume of the tetrahedron is a³, the same formulas conventionally used for squares and cubes. In the 60° system, the tetrahedron is the unit by which volume is measured, and the equilateral triangle is the unit by which surface area is measured.

For example, an equilateral triangle of edge length 4 has an area of 16, or 4×4 smaller triangles. And a regular tetrahedron of edge length 4 has a volume of 64, or 4×4×4 tetrahedra.

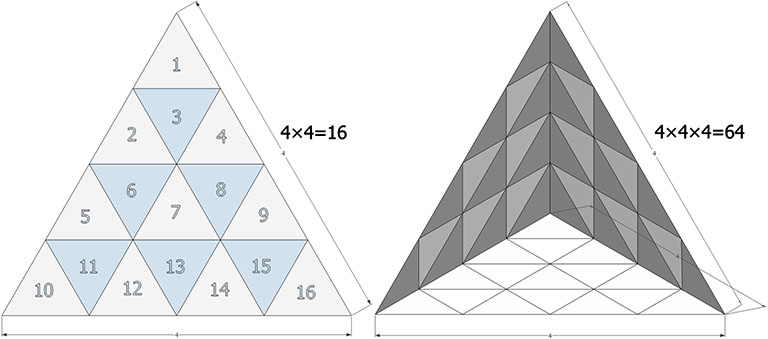
An equilateral triangle subdivided into 16 smaller triangles with 4 triangles to the edge; 4 times 4 equals 16. A regular tetrahedron is subdivided in the same way, with four smaller tetrahedra to the edge. 4 times 4 times 4 equals 64.
60° accounting works just like 90° accounting; the 2nd power of the triangle’s edge length gives its area, and the 3rd power of the tetrahedron’s edge length gives its volume.

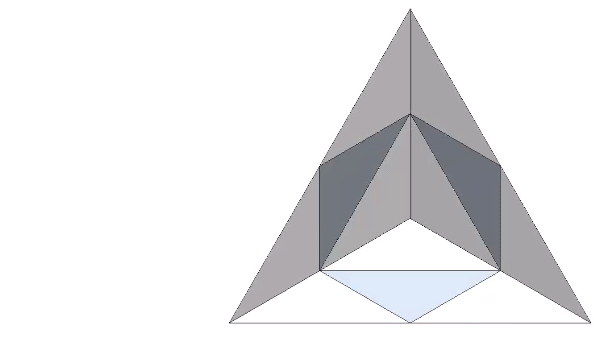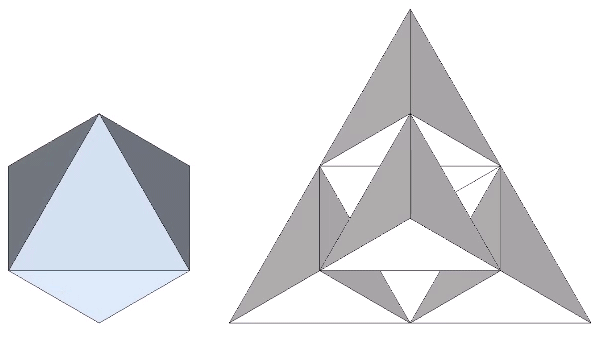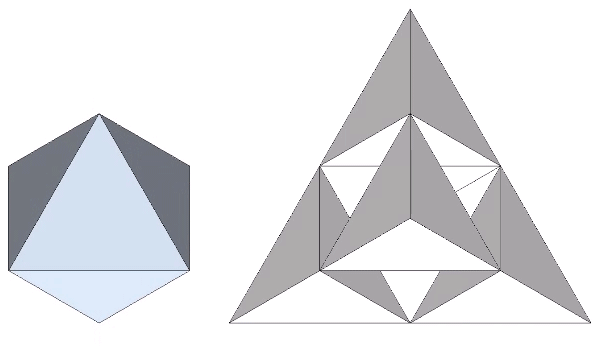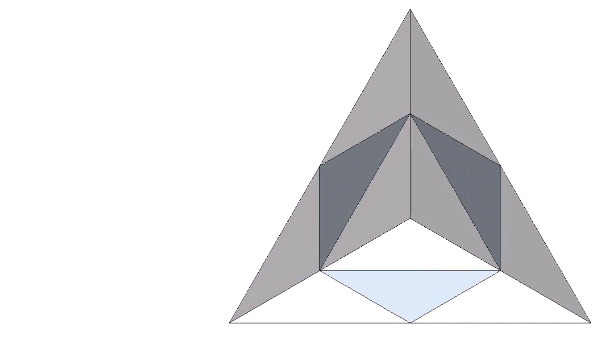
Note that you cannot stack tetrahedra to fill all-space. The large tetrahedron in the above illustration isn’t built of 64 smaller tetrahedra. It is built of a combination of twenty tetrahedra and ten octahedra. Fortunately, the volume of one octahedron is precisely the same as four tetrahedra. 20 + (10×4) = 64.

Subdividing the tetrahedron produces layers of vertex-bonded tetrahedra face-bonded to edge-bonded octahedra. It can be demonstrated operationally that the regular octahedron has a volume of precisely four regular tetrahedra.

To determine the area of a given polygon or the volume of a given polyhedron, we can calculate the area and volume using conventional methods, and then use a conversion factor to find the equivalent area in equilateral triangles or the equivalent volume in tetrahedra. See General Unit Conversions.

Alternatively, we can measure areas and volumes directly, remembering only that the heights differ between the two systems. In conventional geometry, both in plane geometry and in solid geometry, the height is measured at 90° to the base. In 60° geometry, the two-dimensional height is measured at 30° from the perpendicular or 60° from the horizontal base, and the three-dimensional height is measured at arctan(√2/2) from the perpendicular or arctan(√2) from the horizontal base. These are the angles that the edges of the equilateral triangle and tetrahedron make with their respective bases.

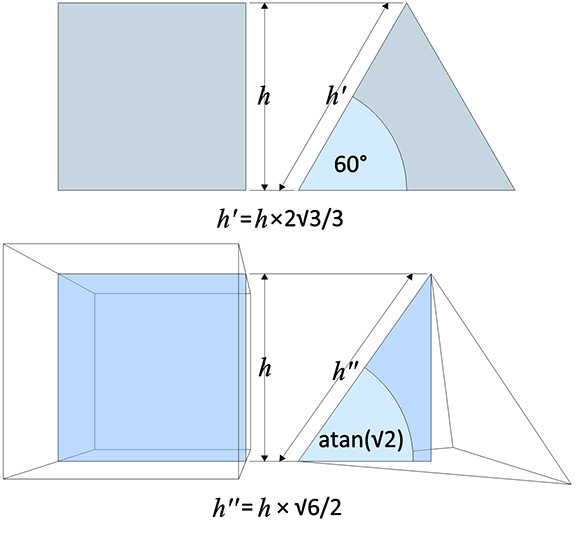
A square whose height, h, is measured at 90 degrees from the horizontal, beside an equilateral triangle whose height, h', is measured at 60 degrees from the horizontal. h' = h times 2√3/3. A cube whose height h is measured at 90 degrees from the horizontal beside a regular tetrahedron whose height, h'', is measured at atan(√2) from the horizontal. h'' = h times √6/2.
In 90° geometry, height (h) is always measured at 90° from the horizontal. In 60° geometry, height in two dimensions (h’) is measured at 60° from the horizontal: h’=h×2√3/3. Height in three dimensions (h”) is measured at arctan(√2) from the horizontal: h”=h×√6/2.

The area for any rhombus (quadrilateral, rectangle, or square) is 2 × base × height, where height is measured at 30° from vertical. Where base = a and the vertical height = h, the formula is:

Triangular area of any rhombus = 2 × a × h2√3/3

Likewise, the area for any triangle is base × height, or, where base = a and h is the vertical height, the formula is:

Triangular area of any triangle = a × h2√3/3

The area for any polygon, regular or irregular, may be calculated by dividing it into rhombuses and/or triangles, calculating the areas of each, and then summing the results. See Calculating Areas of Regular Polygons. The areas of regular polyhedra may be calculated directly from the number sides and the length of its radius. See Calculating Volumes of Regular Polyhedra.

The volume of any polyhedron, regular or irregular, may be calculated by dividing it into cylinders and cones. By cylinders and cones, we mean all cylindrical or conical objects regardless of the shape of their bases. Where h is the perpendicular height…

Tetrahedral volume of a cone = area of base × h × √6/2
Tetrahedron volume of a cylinder = 3 × base × h × √6/2

Examples

Cone with triangular base (Tetrahedron)

This example serves as a proof of the proposition that the volume (in unit tetrahedra) of any regular tetrahedron can be expressed as [edge length]³.

a = edge length
h = height = a√6/3
base (in equilateral triangles) = a²

Volume (in tetrahedra) = base × h√6/2 = a² × (a√6/3 × √6/2) = a³

Cone with Square Base (Half Octahedron)

This example serves as a proof of the proposition that the volume (in unit tetrahedra) of any regular half octahedron can be expressed as 2×[edge length]³.

a = edge length
h = height = a√2/2
base (in equilateral triangles) = a²4√3/3

Volume (in tetrahedra) = base (in equilateral triangles) × h√6/2 = a²4√3/3 × (a√2/2 × √6/2) = 2a³

Cylinder with Square Base (Cube)

This example serves as a proof of the proposition that the volume (in unit tetrahedra) of any cube can be expressed as 3×[length of face diagonal]³.

a = edge length
h = a
d = diagonal = a√2
a = d√2/2
h = d√2/2
base (in equilateral triangles) = 2a×h×2√3/3 = 2(d√2/2)²×2√3/3 = 2d²√3/3

Volume (in tetrahedra) = 3×base (in equilateral triangles)×h = 3×2d²√3/3×(d√2/2×√6/2) = 3d³

Leave a comment