Month: September 2023

Cube

Greg FrederickLeave a comment

“None of the always co-occurring cube’s edges is congruent with the vectorial lines (edges) of the isotropic vector matrix. Thus we witness that while the cubes always and only co-occur in the eternal cosmic vector field and are symmetrically oriented within the field, none of the cubes’ edge lines is ever congruent or rationally equatable with the most economical energetic vector formulating, which is always rational of low number or simplicity as manifest in chemistry. Wherefore humanity’s adoption of the cube’s edges as its dimensional coordinate frame of scientific-event reference gave it need to employ a family of irrational constants with which to translate its findings into its unrecognized isotropic-vector-matrix relationships, where all nature’s events are most economically and rationally intercoordinated with omnisixty-degree, one-, two-, three-, four-, and five- dimensional omnirational frequency modulatability.”
—R. Buckminster Fuller, Synergetics, 982.12

The cube in Fuller’s geometry is conceived as two tetrahedra, one positive and one negative, sharing a common center of volume. In the absence of the triangulation provided by at least one of the tetrahedra, the cube would lack structure and collapse. The length of the face diagonal, rather than the edge length, is therefore taken as unity and produces a cube whose volume is precisely three (3) regular tetrahedra.

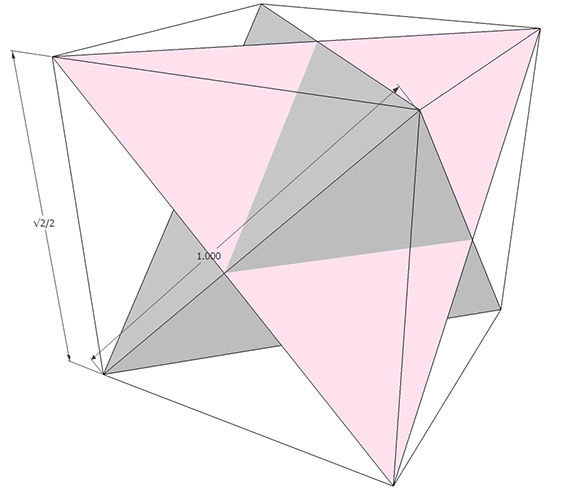
The cube of edge length √2/2 represented as two concentric tetrahedra, one positive and one negative, whose unit-length edges are the cube's diagonals.

The cube, with the face diagonal taken as unit length, d:

  • 6 square faces, 8 vertices, 12 edges
  • Face angles: all 90°
  • Dihedral angle: 90°
  • Tetrahedral volume: 3d³
  • Cubic volume: d³×√2/4
  • Surface area (in equilateral triangles): 8d²√3
  • Surface area (in squares): d²×√2/4
  • A quanta modules: 48
  • B quanta modules: 24
  • In-sphere radius: d×√2/4
  • Mid-sphere radius: d/2
  • Circumsphere radius: d×√6/4

The cube can be constructed from of a regular tetrahedron with four 1/8th octahedra added to its faces.

The unit tetrahedron, consisting of 24 A quanta modules, and four 1/8 octahedra, consisting 6 A and 6 B quanta modules each, combine to form the 3 tetra-volume cube.
The volume-3 cube, shown here in quanta modules, is constructed of one regular tetrahedron with four eighth-octahedra added to its faces.

When we model the isotropic vector matrix as vectors between spheres, the volume-3 cube is indistinguishable from the tetrahedron it encloses.

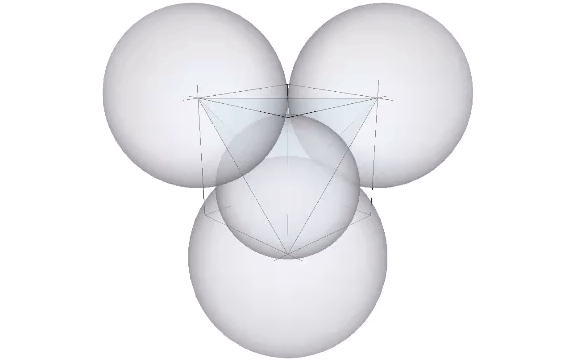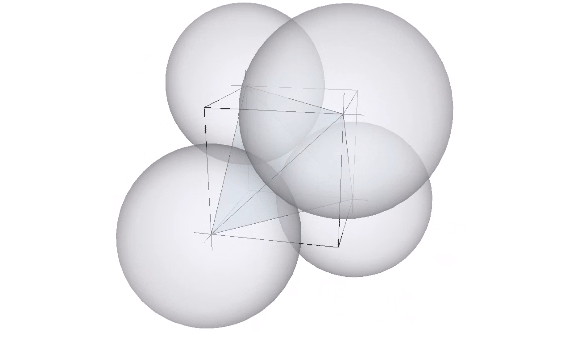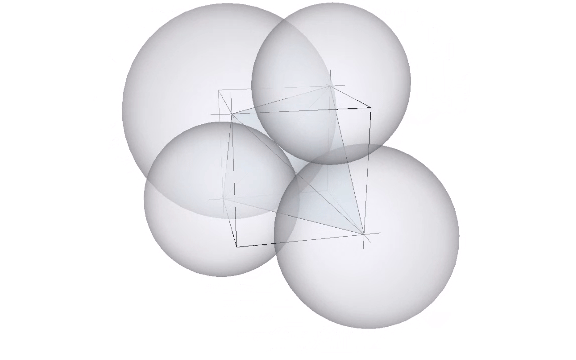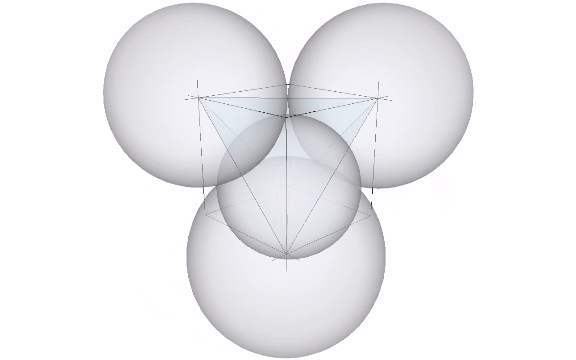
Four spheres occupying the vertices of a unit tetrahedron inscribed inside a cube whose remaining 4 vertices occupy the space between spheres of the isotropic vector matrix.
In the vector-sphere model of the isotropic vector matrix, the volume-3 cube is essentially a tetrahedron.

The cube emerges in the isotropic matrix only at higher frequencies, either by adding four tetrahedra centered on the faces of a larger tetrahedron with twice the edge length, or by adding eight tetrahedra to the eight faces of an octahedron with the same edge length.

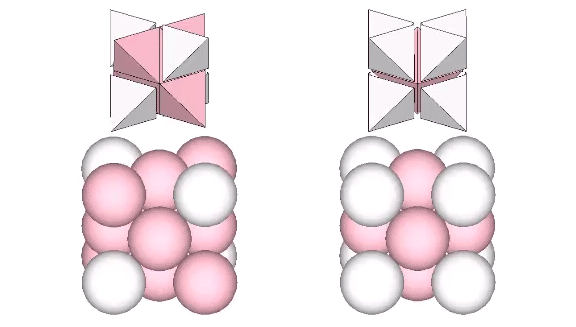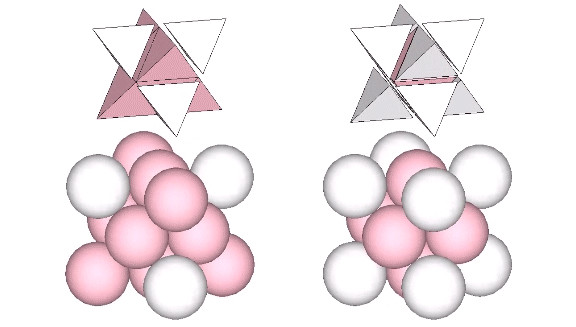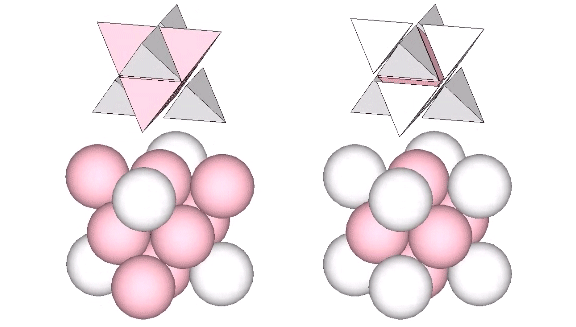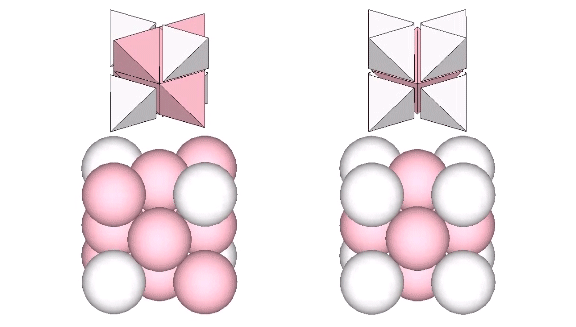
4 spheres (top) or unit tetrahedra (bottom) surmount a 2F tetrahedron (left), 8 spheres (top) or unit tetrahedron (bottom) surmount a 1F octahedron (right).

We can stack eight volume-3 cubes in two configurations to form two larger, distinct, cubes, each of volume-24. From the outside, the difference between these two cubes is subtle. What makes each cube unique is the position each occupies in the isotropic vector matrix. The addition of spheres reveals one to be a cube while the other to be a vector equilibrium (VE).

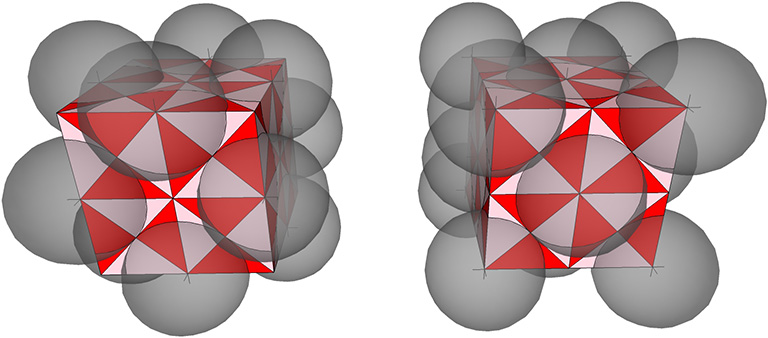
Two configurations of eight 3-tetra-volume cubes stacked around a common center. Transparent spheres occupy the vertices coincident with the isotropic vector matrix. The configuration on the left describes the 1F vector equilibrium with 12 spheres around a nuclear sphere; the configuration on the right describes the 2F cube with 14 spheres around a nuclear space.
Eight volume-3 cubes can be stacked in two configurations resulting two larger cubes occupying different positions in the isotropic vector matrix.

Dissecting the quanta model reveals the VE to contain eight tetrahedra all sharing a common vertex at the center of the vector equilibrium.

24-tetra-volume cube constructed of A and B quanta modules exploding to reveal the eight tetrahedra of the vector equilibrium at its center.
One of the two quanta-module configurations of the the cube reveals eight tetrahedra sharing a common vertex at the center of the VE.

Disecting the quanta model reveals the volume-24 cube to contain eight tetrahedra all rotated at 90° and pointing away from their common center. That is, the two volume-24 cubes constitute the two vector-equilibrium phases of the jitterbug: the VE and the octahedron phases.

24-tetra-volume cube constructed of A and B quanta modules exploding to reveal eight unit tetrahedra surmounting a 1F octahedron.
The other of the two quanta module configurations of the cube reveals eight tetrahedra rotated 90° away from their common center of volume.

At the centers of both cubes is one of the two constructions of the rhombic dodecahedron, one modeling the nuclear sphere, and the other the nuclear space. See: Spheres and Spaces; and Quanta Module Constructions of the Rhombic Dodecahedron.

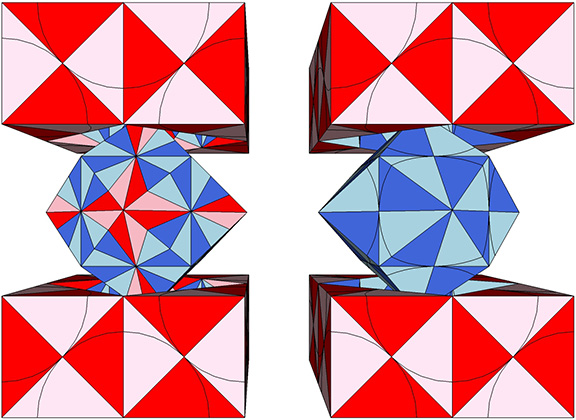
Two configuration of the 24-tetra-volume cubes constructed of A and B quanta modules. Each is divided horizontally to reveal a rhombic dodecahedron at its center. The configuration on the left reveals the rhombic dodecahedron associated with the sphere. The configuration on the right reveals the rhombic dodecahedron associated with the space between spheres.

In the quanta model of the isotropic vector matrix, the two cubes overlap. One or the other is revealed depending on how we slice the matrix. When modeled as the radial close packing of spheres, however, the two cubes form discrete modules that close pack to fill the matrix.

The isotropic vector matrix divided into four each of two clusters, one with 12 spheres surrounding a central sphere, and the other with 14 spheres surrounding a space.

The two exchange places during the jitterbug transformation, i.e., one transforms into the other. Each gains or loses a sphere in the process, suggesting the migration of nuclei.

Eight unit tetrahedra sharing a common vertex are rotated 90 degrees to exchange their common vertex for a 1F octahedron. As the tetrahedra rotate, the spheres move from the center of one to the periphery of the other, and vice versa.
The transformation of the two cubes in the jitterbug suggests the migration of nuclei.

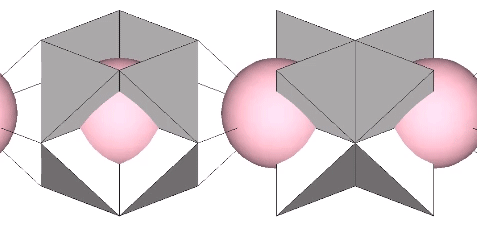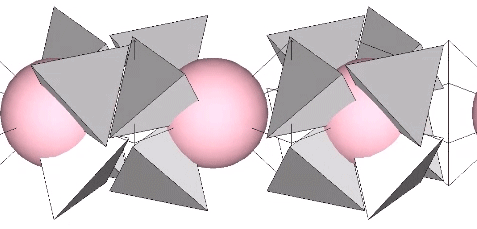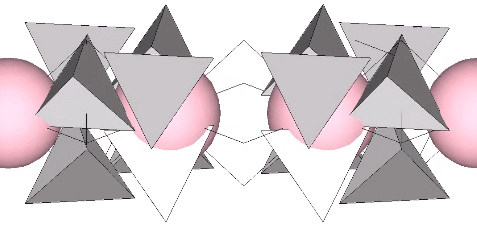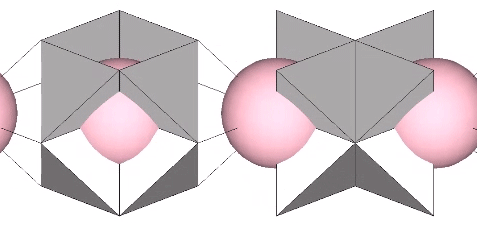
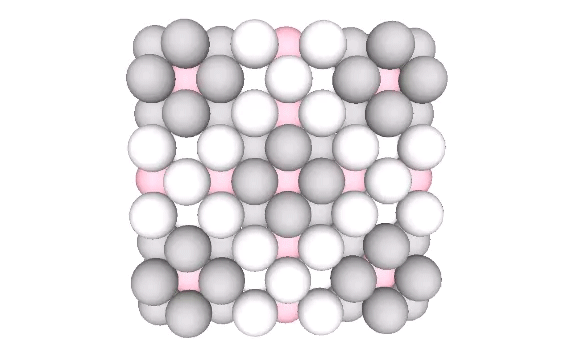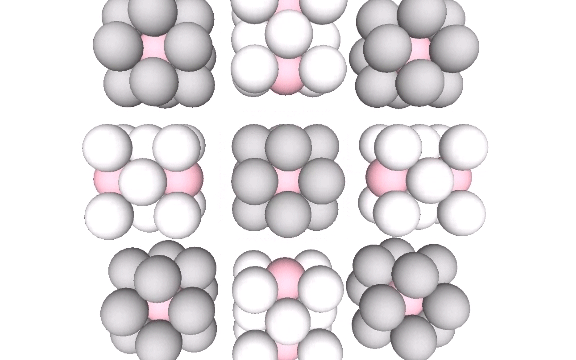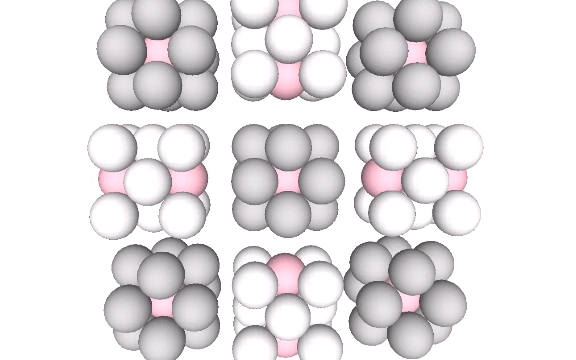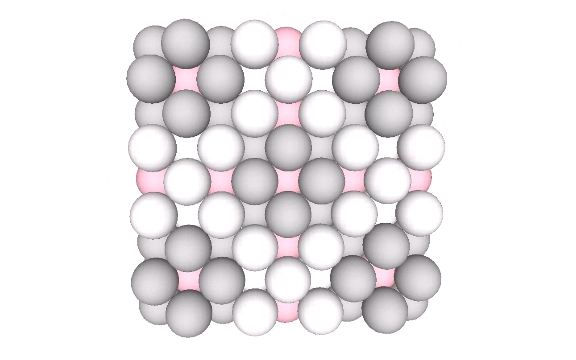
Spheres close pack as cubes in even-numbered layers around octahedra (spaces) and VEs (spheres). In odd-numbered layers, the spheres form partially-truncated cubes surrounding a positive or negative tetrahedron (interstice). The growth pattern repeats every fourth layer, with the first layer surrounding a positive (or negative) tetrahedron; the second layer surrounding an octahedron (or VE); the third layer surrounding a negative (or positive) tetrahedron, and; the fourth layer surrounding a VE (or octahedron).

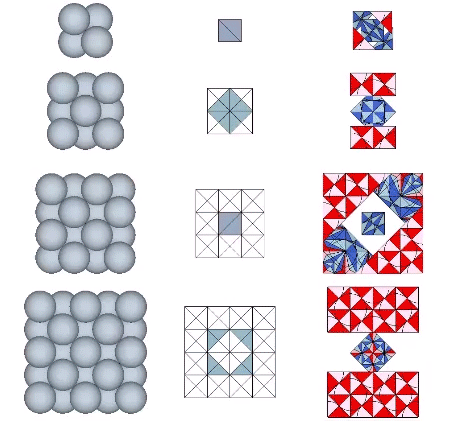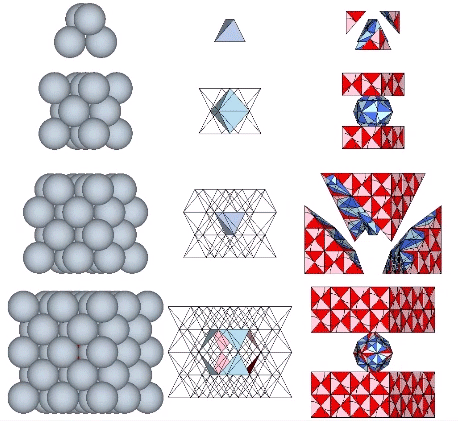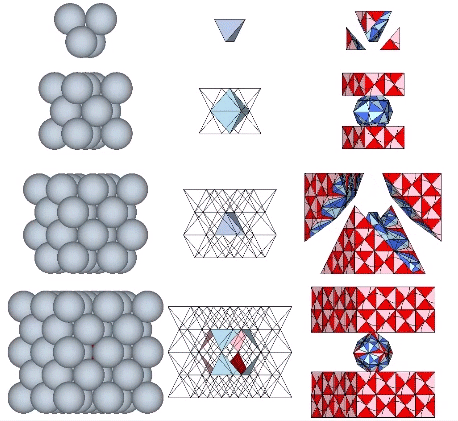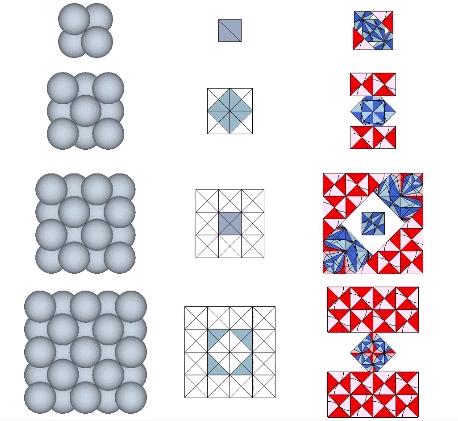
1F, 2F, 3F, and 4F cubes modeled as close-packed spheres, vectors, and quanta modules. The quanta models are bisected horizontally to reveal the following: at the center of the 1F cube is a positive regular tetrahedron; at the center of the 2F cube is rhombic dodecahedron space; at the center of the 3F cube is a negative regular tetrahedron; at the center of the 4F cube is a rhombic dodecahedron sphere. Odd layers produce partially truncated cubes which is evident only in the sphere and vector models.
Close-packed spheres form cubes in even layers with either a sphere or a space at their centers. Odd layers produce partially truncated cubes with either a positive or negative tetrahedron at their centers. The pattern repeats every four layers.

Note that the cube’s edges, no matter the frequency, never align to the vectors connecting sphere centers in the isotropic vector matrix. Only its face diagonals are congruent with the matrix vectors.

Fuller thought that the vector-edged cube and the icosahedron had a combined “energetic” volume (or volume in regular tetrahedra) of 3³, or 27. Actually, their combined volume is just under 27, about 26.997577.

energetic volume of icosahedron = V³×5φ²/6 ≈ 18.5122959
energetic volume of vector-edge cube = V³ ≈ 8.4852814
combined volume = V³×5φ²/6 + V³ ≈ 26.997577

The constant, V, is Fuller’s dymaxion vector constant which equals 2 × ⁶√(9/8), or about 2.039648903. For more information on calculating “energetic” volumes, see Pi and the Synergetics Constants.