The Geometry of Thinking

See also: The 31 Great Circles of the Icosahedron (new illustrations).

“The 31 great circles of the icosahedron always shunt the energies into local-holding great-circle orbits, while the vector equilibrium opens the switching to omni-universe energy travel. The icosahedron is red light, holding, no-go; whereas vector equilibrium is green light, go. The six great circles of the icosahedron act as holding patterns for energies. The 25 great circles of the vector equilibrium all go through the 12 tangential contact points bridging between the 12 atomic spheres always closest packed around any one spherical atom domain.”
— R. Buckminster Fuller, Synergetics, 1132.02

“The six great circles of the icosahedron are the only ones not to go through the potential inter-tangency points of the closest-packed unit radius spheres, ergo energy shunted onto the six icosahedron great circles becomes locked into local holding patterns, which is not dissimilar to the electron charge behaviors.”
— ibid. 457.22

In Fuller’s energetic geometry, the great circles of the VE and icosahedron model energy transference and containment. He described them as “railroad tracks” which either move energy from one domain to another, or divert energy into into loops or holding patterns. Communication occurs when a great circle of one sphere crosses a great circle of an adjacent sphere, i.e. crosses a point of contact or, in Fuller’s terminology, a “kissing point.” All of the 25 great circles of the VE intersect at least two points of contact with neighboring spheres. This is consistent with the role of the VE in the isotropic vector matrix and what Fuller called “nature’s coordinate system.” Of the 31 great circles of the icosahedron, only 7 intersect with the isotropic vector matrix, and these are identical with the sets of 3 and 4 great circles of the VE and the seven axes of symmetry. This isolation is consistent with Fuller’s conception of the icosahedron as a model of potential energy or charge. Of the remaining 24 great circles of the icosahedron, 18 interse ct with adjacent spheres only when close-packed as icosahedral shells, and 6 are true holding patterns, communicating with neither the isotropic vector matrix of radially close-packed spheres, nor with the icosahedron shells of laterally close-packed spheres. (See: Close-Packing of Spheres)

The 10 face-to-face axes, the 15 edge-to-edge axes, and the 6 vertex-to-vertex axes define the 31 great circles of the icosahedron.

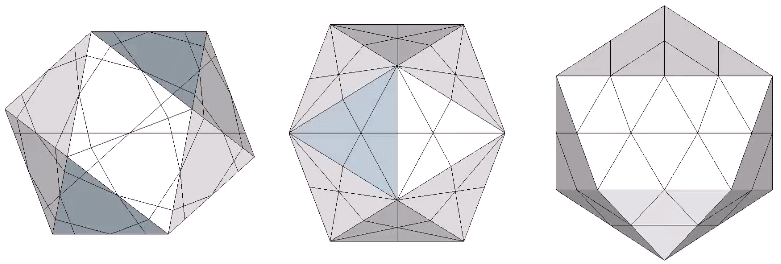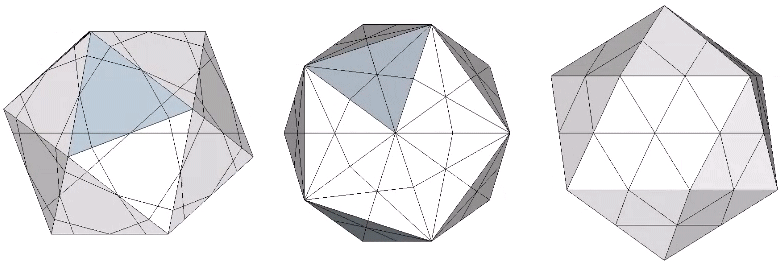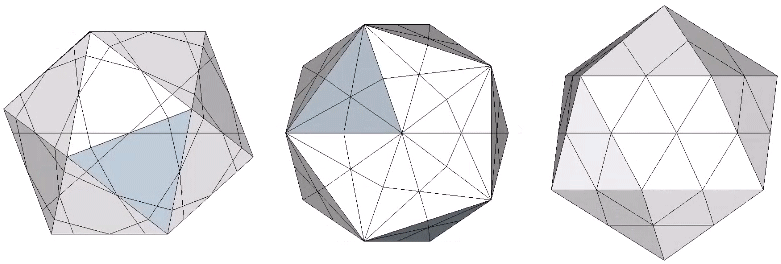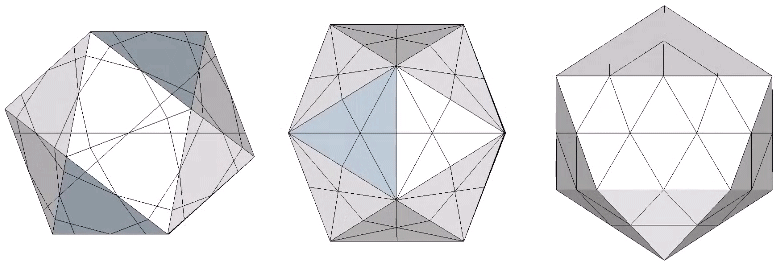
The 31 great circles of the icosahedron disclose the following spherical polyhedra: octahedron; icosahedron; pentagonal dodecahedon; icosidodecahedron; tricontahedron; and VE. See Icosahedron: Spherical Polyhedra Disclosed by Great Circles.

Only seven of the 31 great circles of the icosahedron pass through points of contact between the radially close-packed spheres of the isotropic vector matrix. Their axes are the identical with Fuller’s Seven Axes of Symmetry. These include 4 of the 10 great circles defined by the ten face-to-face axes of the icosahedron (these are the same 4 associated with the VE’s triangular face-to-face axes), and 3 of the 15 great circles defined by the fifteen edge-to-edge axes of the icosahedron (these are the same 3 associated with the VE’s square face-to-face axes). (See: The 25 Great Circles of the Vector Equilibrium.) All of the great circles which are unique to the icosahedron pass through none of the points of contact between the radially close-packed spheres, and are therefore what Fuller called “local-holding great-circle orbits.”

The 15 great circles of the icosahedron each pass through four of the twelve vertices of the icosahedron, and therefore provide communication between spheres close-packed as discrete icosahedron shells or lattices (See: Close Packing of Spheres, and Close Packing of Icosahedra. The 6 great circles of the icosahedron pass through neither the vertices of VE nor those of the icosahedron, and are therefore true holding patterns, providing no inter-sphere communication.

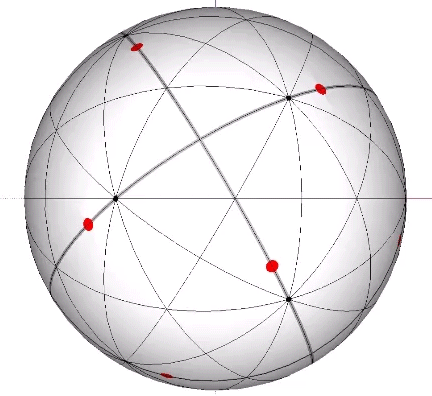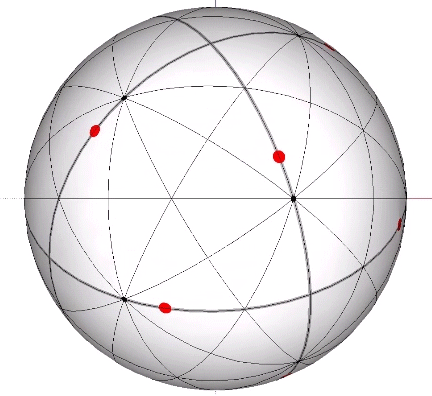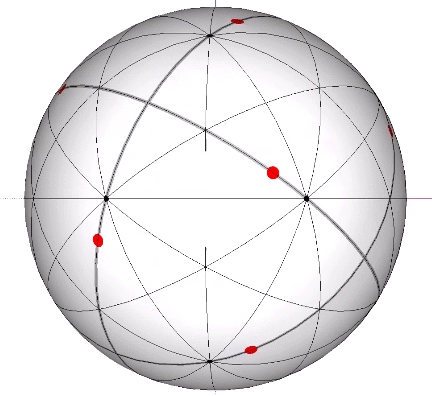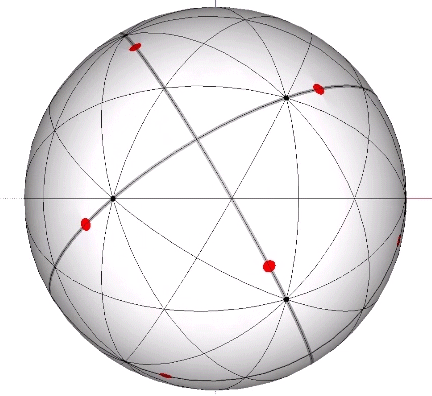
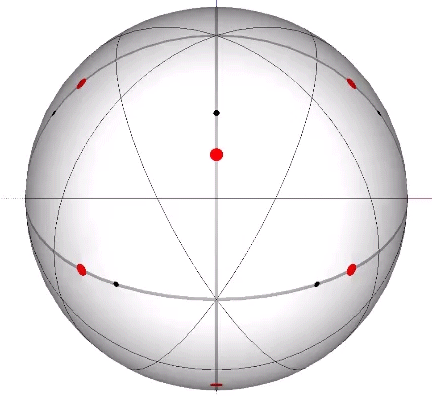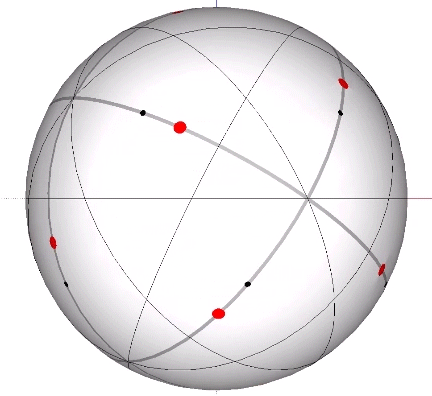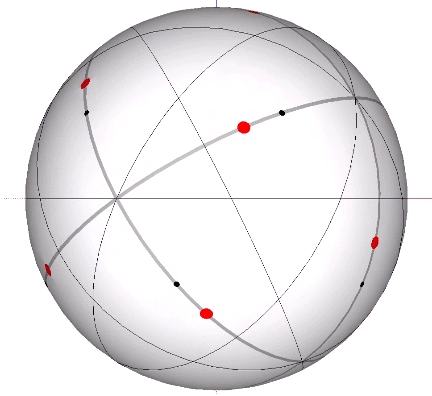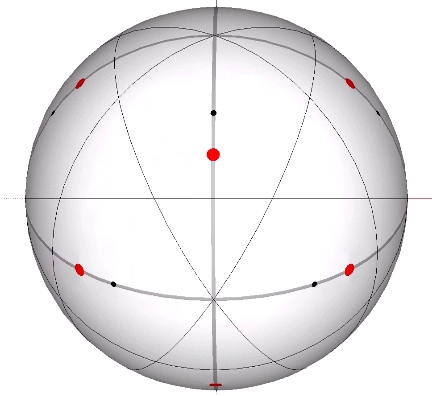
In the figures below, the referenced great circles are indicated by the thin black lines, the points of contact between radially close-packed spheres of the isotropic matrix, or the vertices of the VE, are indicated by red dots. The points of contact between spheres close-packed into discrete icosahedral shells or lattices, or vertices of the icosahedron, are indicted by black dots. The paths followed by the vertices in the jitterbug transformation are indicated by thick gray lines.

Set of 15 (Axes Connect Opposing Edges)

The 15 great circles defined by the set of fifteen edge-to-edge axes of the icosahedron disclose the spherical pentagonal dodecahedron and the Basic Disequilibrium LCD Triangle. Each of the fifteen great circles passes through four of the twelve vertices of the icosahedron, and each vertex of the icosahedron connects with five great circles. Three of the fifteen pass through the vertices of the VE, and these are identical with the VE’s 3 great circles defined by its three square face-to-face axes of spin.

Set of 10 (Axes Connect Opposing Faces)

The 10 great circles defined by the set of ten face-to-face axes of the icosahedron disclose the spherical vector equilibrium (VE). None pass through the vertices of the icosahedron. Four pass through the vertices of the VE, and these are identical with the VE’s 4 great circles which describe the spherical VE.

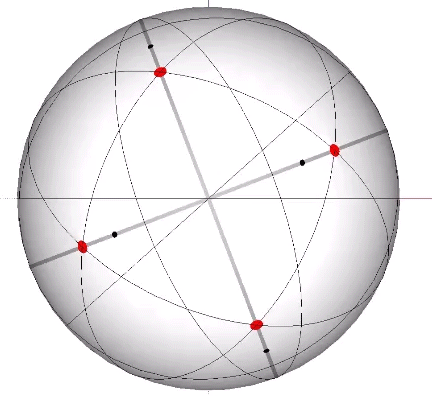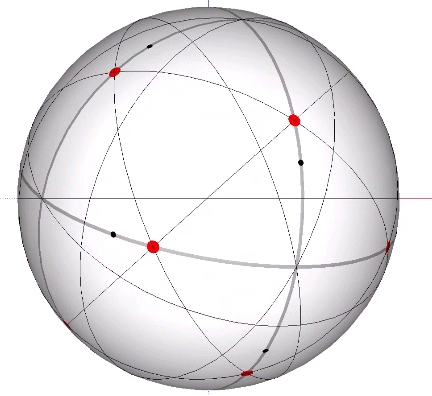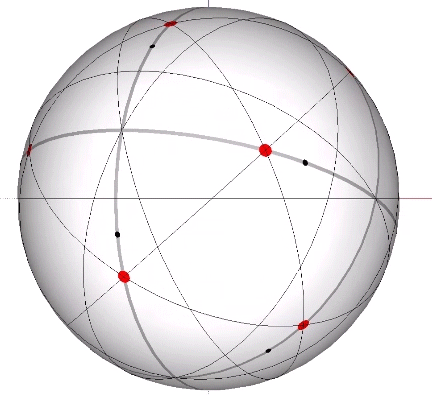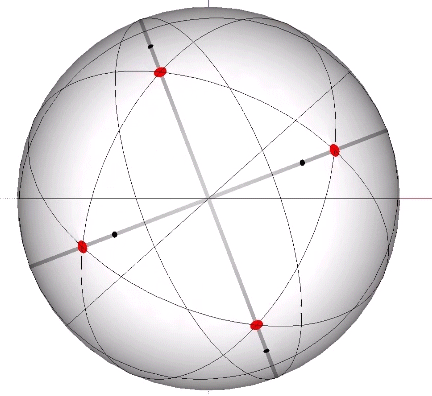
Set of 6 (Axes Connect Opposing Vertices)

The 6 great circles defined by the set of six vertex-to-vertex axes of the icosahedron disclose the spherical icosidodecaheron, the 42-sided polyhedron associated with the spherical form of the 30-strut tensegrity icosahedron. (See: Tensegrity.) None pass through a vertex, neither of the VE nor of the icosahedron, and therefore provide no inter-sphere communication.

For discussion on the surface and central angles described by the 31 great circles of the icosahedron, see Basic Disequilibrium LCD Triangle.