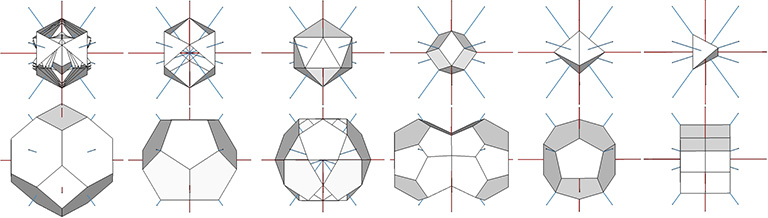
Fuller has two definitions for his “seven axes of symmetry.” The first definition relates to the great circle sets of the vector equilibrium (VE) and the icosahedron. The 25 great circles of the VE are defined by four sets of axes, and the 31 great circles of the icosahedron are defined by three sets of axes. 4+3=7.
The second definition applies to a subset of the first. Fuller noted that truncations through the vertices and edges of the regular tetrahedron produces a tetrakaidecahedron with six square and eight hexagonal faces. (Truncating the faces will produce only a smaller tetrahedron.) The tetrakaidecahedron has fourteen faces, lines through the centers of which define seven axes of spin. Coordinated truncations produce the Kelvin truncated octahedron, which is associated with nuclear domains in the isotropic vector matrix, and with the optimal cellular packing of the Weaire-Phelan matrix (see Tetrakaidecahedron and Pyritohedron).
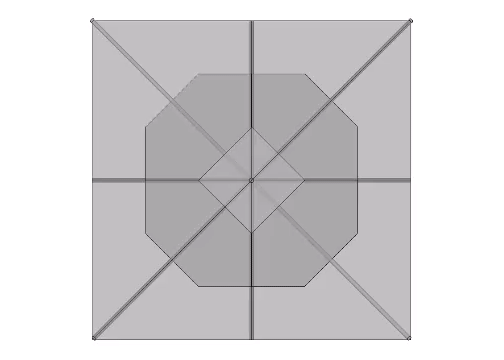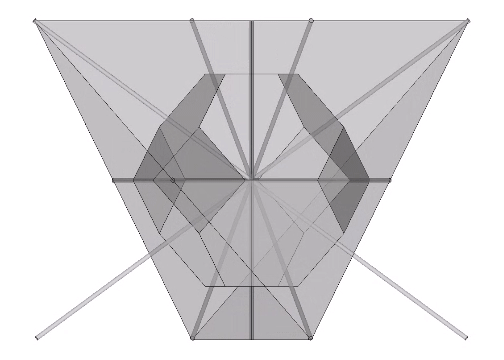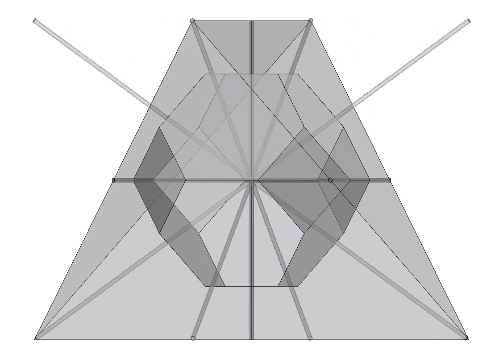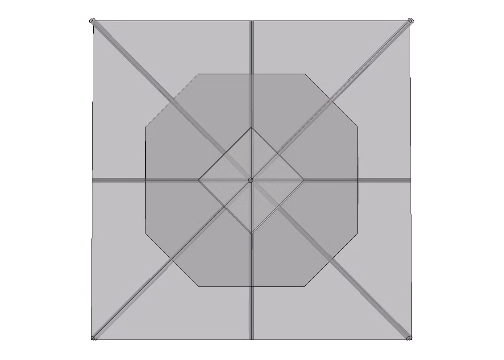
The Seven Axes of Symmetry are identical with the seven face-to-face axes of the VE, and correspond to four of the icosahedron’s ten face-to-face axes and three of its fifteen edge-to-edge axes. The great circles defined by the set of 4 axes discloses the spherical VE (red in the figure below), and the great circles defined by the set of 3 axes defines the spherical octahedron (blue in the figure below).

All the regular polyhedra, as well as other polyhedra significant to Fuller’s geometry, align with the Seven Axes of Symmetry.