The Geometry of Thinking

“When the centers of equiradius spheres in closest packing are joined by most economical lines, i.e., by geodesic vectorial lines, an isotropic vector matrix is disclosed, ‘isotropic’ meaning “everywhere the same,” ‘isotropic vector’ meaning “everywhere the same energy conditions.” This matrix constitutes an array of equilateral triangles that corresponds with the comprehensive coordination of nature’s most economical, most comfortable, structural interrelationships employing 60-degree association and disassociation. Remove the spheres and leave the vectors, and you have the octahedron-tetrahedron complex, the octet truss, the isotropic vector matrix.”
— R. Buckminster Fuller, Synergetics, 420.01

“Euclid was not trying to express forces. We, however … are exploring the possible establishment of an operationally strict vectorial geometry field, which is an isotropic (everywhere the same) vector matrix. We abandon the Greek perpendicularity of construction and find ourselves operationally in an omnidirectional, spherically observed, multidimensional, omni-intertransforming Universe.”
— ibid. 825.28

The vector equilibrium (VE) and the isotropic vector matrix constitute the core of Fuller’s geometry. Its discovery is one of Fuller’s earliest memories, from a kindergarten class in his childhood home of Milton, Massachusetts. Given semi-dried peas and toothpicks, and a visual deficit as yet uncorrected by the strong glasses he wore all his life, he fumbled sightlessly, and through touch alone constructed what he would later name the octet truss. His classmates constructed cubes and the gabled house-like shapes they were familiar with. Fuller constructed something that satisfied his sense of touch rather than his sense of sight, a sense which could easily have been prejudiced by the cubes and right angles of his built environment. Instead, his fingers naturally sought out and found the triangle, the tetrahedron, and the octahedron, arrangements which, unlike squares and cubes, held their shape and could not be deformed. He credits his kindergarten teacher, Miss Parker of Milton, Massachusetts, with the discovery; it was her praise and kind remarks that fixed the experience in his memory and, eventually, would inspire a lifelong critique of conventional geometry, and his explorations into the energetic-synergetic geometry of nature.

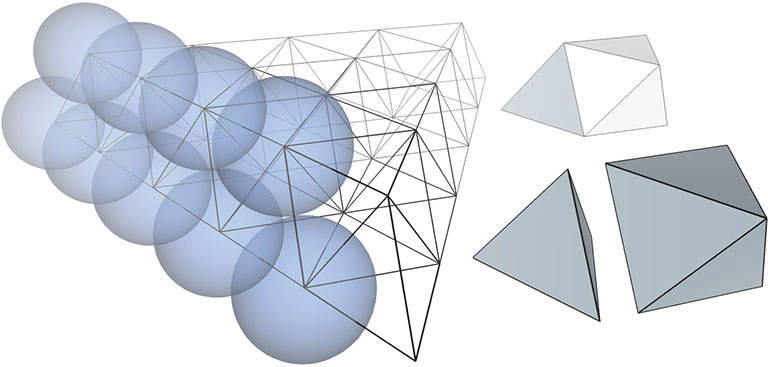
The isotropic vector matrix is the geometric analog to Fuller’s more general statement of Avogadro’s proposition, that “under identical, unconstrained, and freely self-interarranging conditions of energy all elements will disclose the same number of fundamental somethings per given volume.” Fuller’s geometry replaces the abstract concept of infinite lines and line segments with the physical concept of energy vectors. A geometric model of Avogadro’s equilibrium state must have all energy vectors of equal length, i.e. equal products of mass times velocity, and all interacting at the same angles. All vectors in the isotropic vector matrix therefore are of equal length, i.e. the diameter (or two times the radius) of the uniform sphere, and all interact with the others at exactly 60°.

Construction can be accomplished by vertex-bonded (positive or negative) tetrahedra, or by edge-bonded octahedra. Positive-tetrahedron or negative-tetrahedron constructions (but not both) produce a matrix of single vectors, while the octahedron constructions produce a matrix of doubled vectors. Edge-bonding positive and negative tetrahedron together produces a doubled-vector matrix complementary to the doubled-vector octahedron construction.

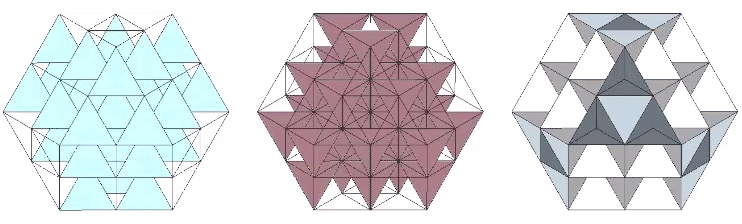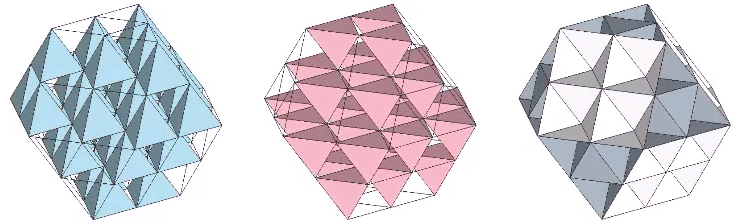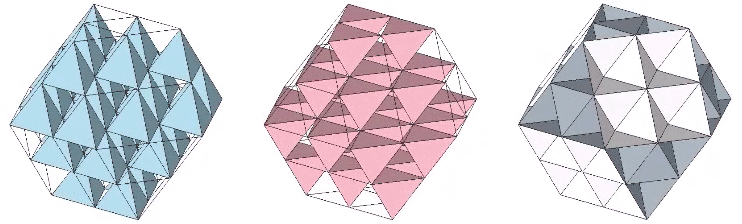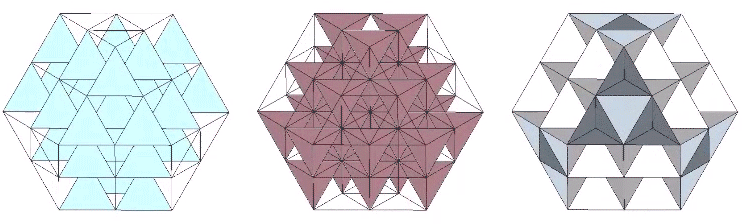
Each of the two constructions (edge-bonded positive and negative tetrahedra, and edge-bonded octahedra) can be transformed into the other by turning themselves inside out. Note that this inside-out transformation results in the same matrix, one emphasizing the tetrahedra and the other emphasizing the octahedra; there is no shifting of vertices or exchanging of spheres and spaces as in The Jitterbug transformations.

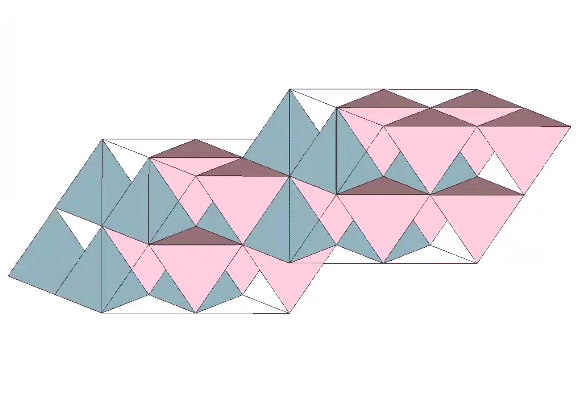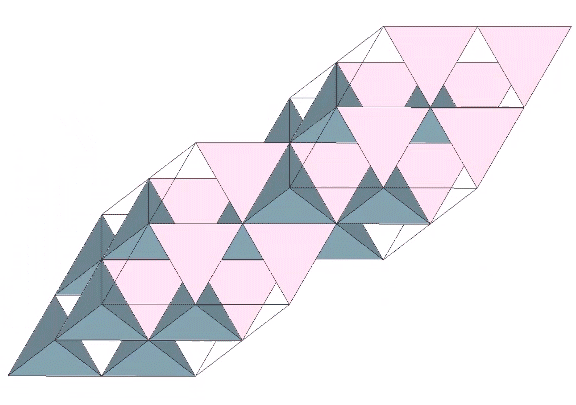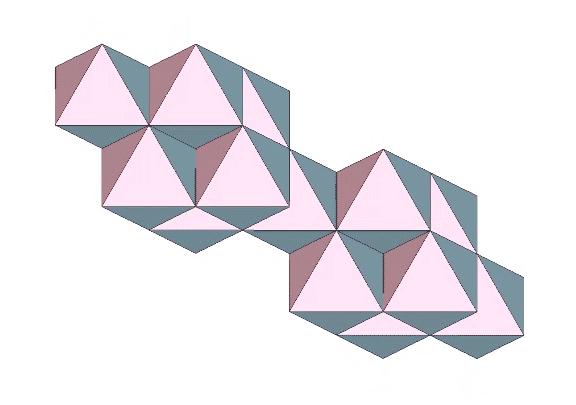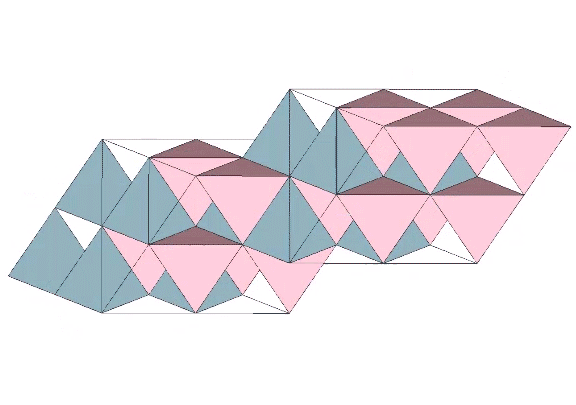
All of the models of the isotropic vector matrix can be broken down into the following:

1. spheres,
2. spaces, and;
3. interstices.

In the vector model, the sphere is represented by the vector equilibrium (VE), the space by the octahedron, and the interstices by positive and negative tetrahedra. In the quanta model, spaces and spheres are represented by the two constructions of rhombic dodecahedron, and the interstices appear as tetrahedra or cubes. In the spheres and interstitial models, the spheres are represented, obviously, by spheres, the spaces are represented by concave VEs inside of the octahedra, and the interstices are represented as concave octahedra inside of the tetrahedra.

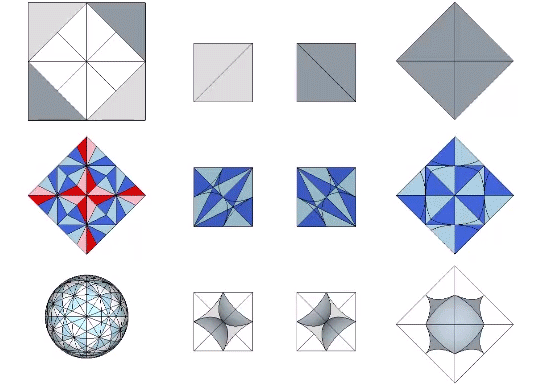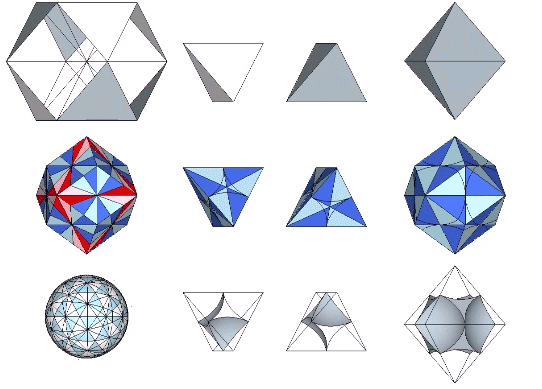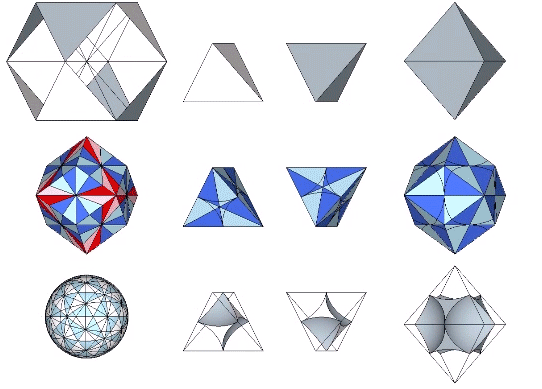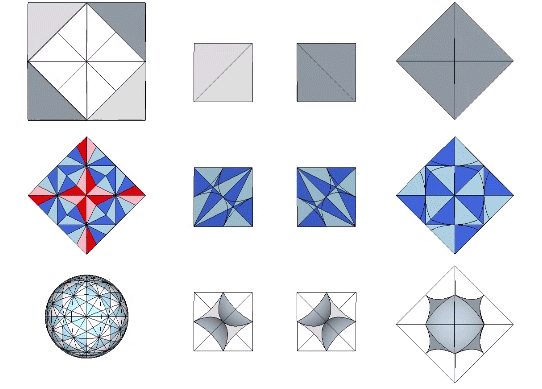
See also: Spheres and Spaces; A and B Quanta Modules; and Quanta Module Constructions of the Rhombic Dodecahedron.