Kelvin Truncated Octahedron

Greg Frederick

“The tetrakaidecahedron (Lord Kelvin’s “Solid”) is the most nearly spherical of the regular conventional polyhedra; ergo, it provides the most volume for the least surface and the most unobstructed surface for the rollability of least effort into the shallowest nests of closest-packed, most securely self-cohering, allspace- filling, symmetrical, nuclear system agglomerations with the minimum complexity of inherently concentric shell layers around a nuclear center.“
—R. Buckminster Fuller, Synergetics, 942.70

The Kelvin truncated octahedron, or Kelvin, is a space-filling, fourteen-sided polyhedron with eight hexagonal faces and six square faces, all of equal edge-length. It got its name from a problem posed by Lord Kelvin in the 19th century, to find an arrangement of cells of equal volume so that their total surface area is minimized.

The vertices of the regular octahedron (left) are truncated to construct the Kelvin, or truncated octahedron, (right).
The six vertices of the regular octahedron (left) are truncated to create the six square faces of the Kelvin (right).

Note: Fuller refers to this shape as the tetrakaidecahedron, a generic term for all 14-sided polyhedra. I reserve this term for the all-space filling complement to the pyritohedron in the Weire-Phelan matrix. See Tetrakaidecahedron and Pyritohedron.

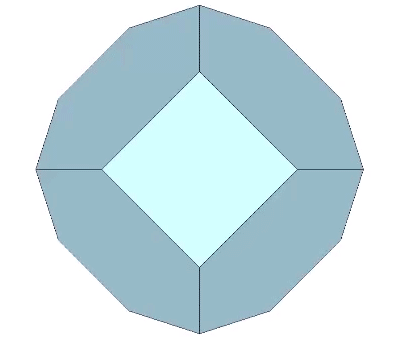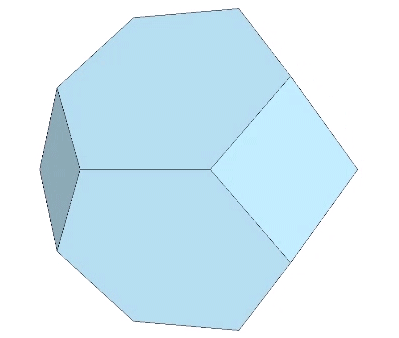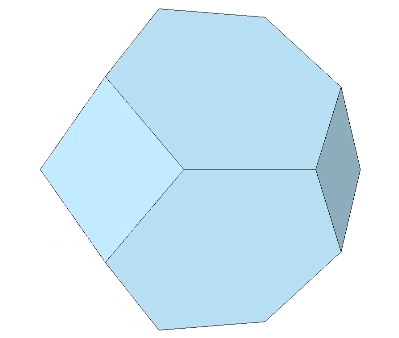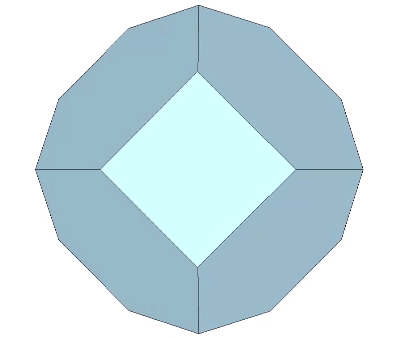
The Kelvin, with eight hexagonal faces and 6 square faces, all of equal edge length.
This truncated octahedron was proposed by Lord Kelvin as the solution to the Kelvin problem: How can space be partitioned into cells of equal volume with the least area of surface between them?

Angles and dimensions of the Kelvin tetrakaidecahedron or truncated octahedron with edge length a:

  • 14 faces (8 hexagonal and 6 square), 24 vertices, 36 edges
  • Face angles: 90°, 120°, 120°
  • Dihedral angle: arccos(-√3/3) ≈ 125.264390°
  • Central angle of edge: atan(3/4) ≈ 36.869898°
  • Volume (in tetrahedra): 96a³
  • Volume (in cubes): 11a³√2
  • A quanta modules: 1,536
  • B quanta modules: 768
  • Surface area (in equilateral triangles): 8a²(6+√3)
  • Surface area (in squares): 6a²(1+2√3)
  • In-sphere radius (center to mid-hexagonal-face): a√(3/2) = a√6/2
  • In-sphere radius (center to mid-square face): a√2
  • Mid-sphere radius (center to mid-edge): 3a/2
  • Circumsphere radius (center to vertex): a√(5/2)
A semi-transparent Kelvin, with radii, dihedral angle and central angle indicated.
Kelvin Truncated Octahedron, central angle, in-sphere, mid-sphere, and circum-sphere radii.

Fuller noted that the Kelvin defined nuclear domains in the radial close-packing of unit-radius spheres.

14 transparent Kelvins enclosing the 14 nuclei and their 12-sphere shells that surround a central nucleus and its 12-sphere shell.
The fourteen sided Kelvin Structure encloses nuclear domains in the radial close-packing of unit-radius spheres.

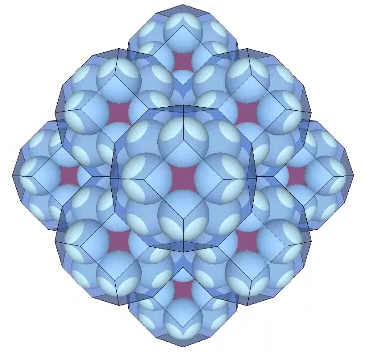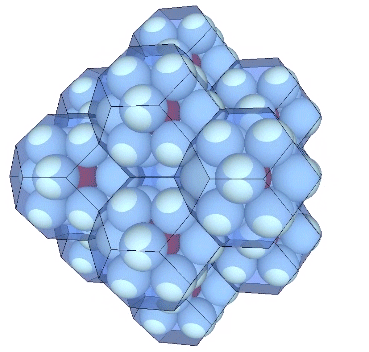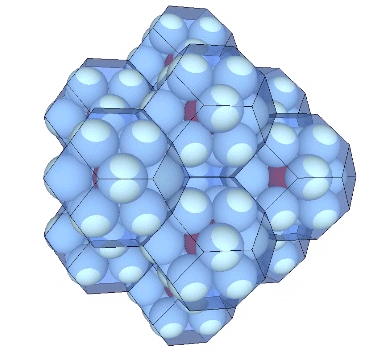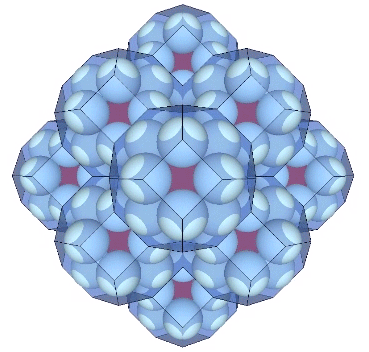
Presently the best solution to the Kelvin problem is the Weaire-Phalen matrix, consisting of pyritohedra and tetrakaidecahedra. Perhaps not surprisingly, the Kelvin can be derived from from this matrix. Connecting radials of the tetrakaidecahedra forms the very same Kelvin as above. Its edges are of unit-length, the same as the spheres’ diameters.

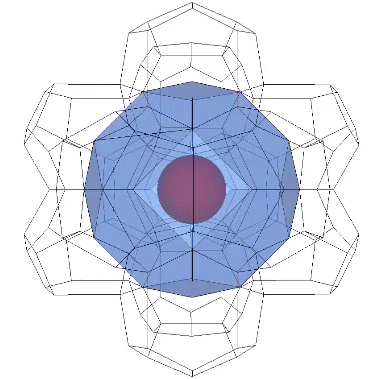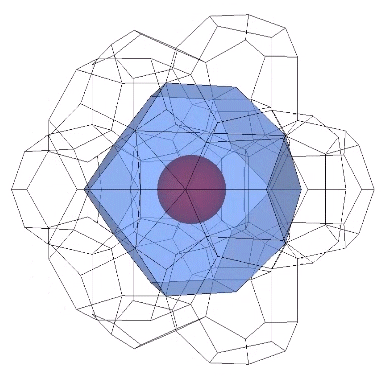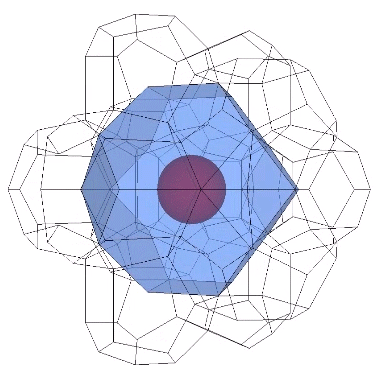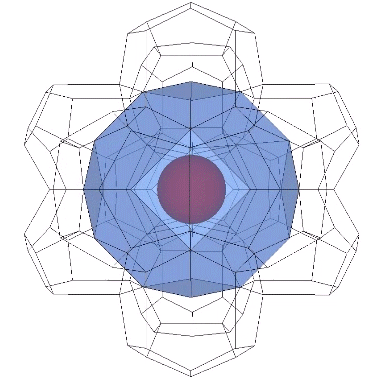
A nucleus at the center of a vector model of the Weaire-Phelan matrix consisting of one pyritohedron surrounded by 12 tetrakaidecahedra. Radials of the tetrakaidecahedra connect to form a semi-transparent blue Kelvin enclosing the pyritohedron and the nucleus at its center.
Connecting the radials of the tetrakaidecahedra in the Weaire-Phelan matrix defines the nuclear domain as the Kelvin truncated octahedron

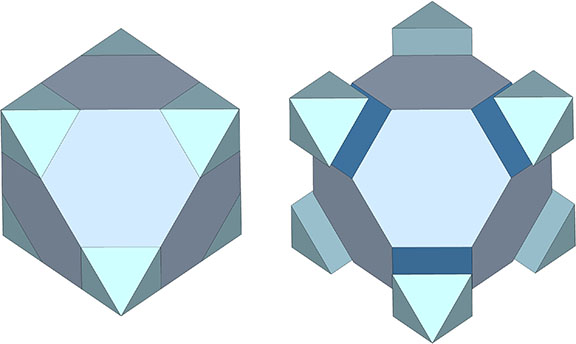
It may be easier to see how the Kelvin faces are derived from the radials of the tetrakaidecahedron if we examine one of its square faces and one of its hexagonal faces individually. The pink spheres in the illustrations below are the non-unique nuclei, those nuclei whose shells are shared with their neighbors. See Formation and Distribution of Nuclei in Radial Close-Packing of Spheres.

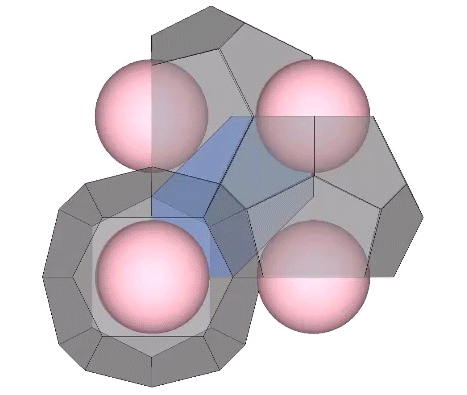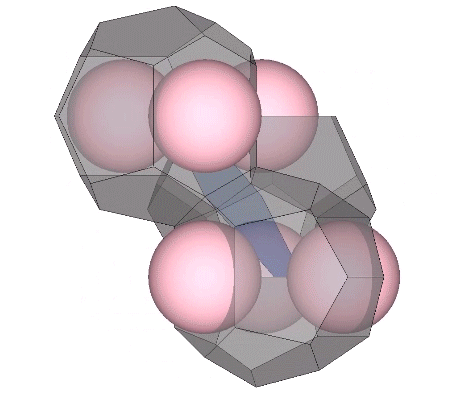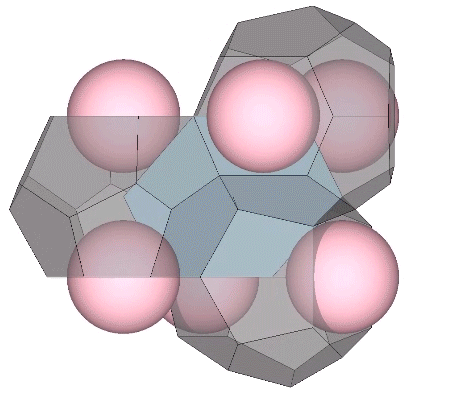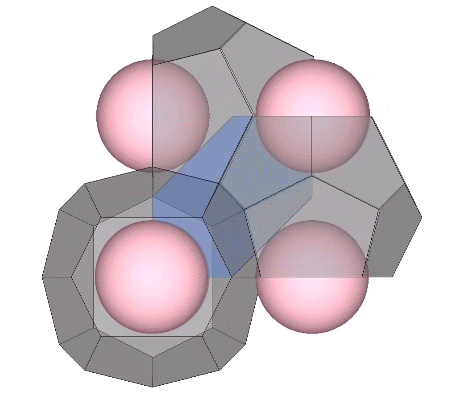
Three tetrakaidecahedra, their 6 non-unique nuclei, with the hexagonal face of a Kelvin at their common center.
Connecting the radials of three adjacent tetrakaidecahedra (face-bonded on their elongated pentagonal faces) describes the hexagonal face of the Kelvin.
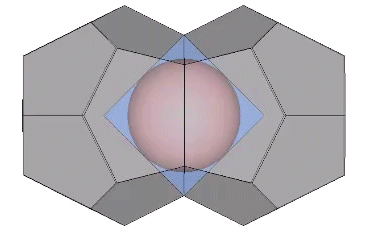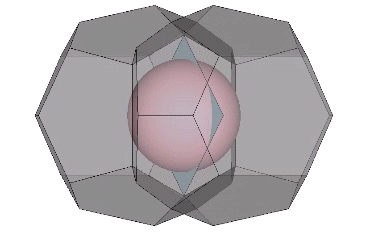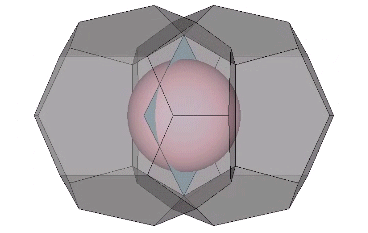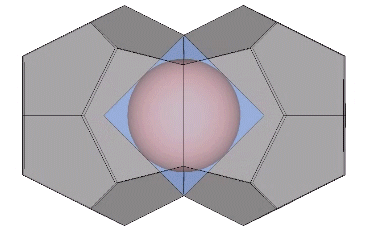
Two tetrakaidecahedron, face bonded on their hexagonal face, with a non-unique nucleus and the square face of a Kelvin at their common center.
Connecting the radials of two adjacent tetrakaidecahedra (face-bonded on their hexagonal faces) describes the square face of the Kelvin.

The two in-sphere radii—from center to mid-square-face, and from center mid-hexagonal-face—make an angle of arctan(√2) ≈ 54.735610° with each other. A line drawn between the mid-faces creates an isosceles triangle with a base of a√2 and sides of a√(3/2). Extending the mid-hexagon-face radius to where it crosses a line drawn perpendicular from the mid-square-face radius creates an isosceles triangle with a base of 2a (where a = edge length, unity, or sphere diameter) and sides of a√(3/2). Combining the two isosceles triangles creates a right triangle whose legs measure a√2 and 2a, and whose hypotenuse measures 2×a√(3/2) = a√6.

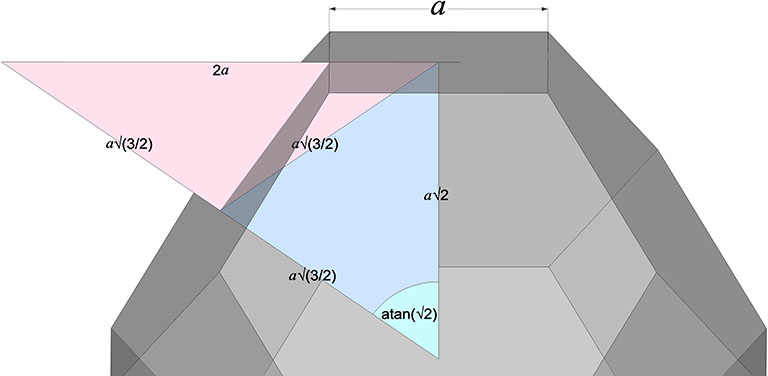
The Kelvin with an isosceles triangle formed by the in-sphere radii, and second isosceles triangle formed the chord between them, and the extension of the radius through the hexagonal face to where it crosses a perpendicular to the radius to mid-square-face radius.
The two midsphere radii form an isosceles triangle. Extending the mid-hexagon-face to precisely twice its length forms a right triangle with a perpendicular to the mid-square-face radius.

This triangle maps to the distribution of nuclei in the isotropic vector matrix, with unique nuclei centered on the vertices of the two non-right angles, and the nuclei that share their shells with adjacent nuclei centered on the right angle’s vertex.

Note that in the illustrations below, d = a = the sphere diameter. Unique nuclei are colored red, non-unique nuclei are pink, and the spheres occupying the shells of nuclei are white.

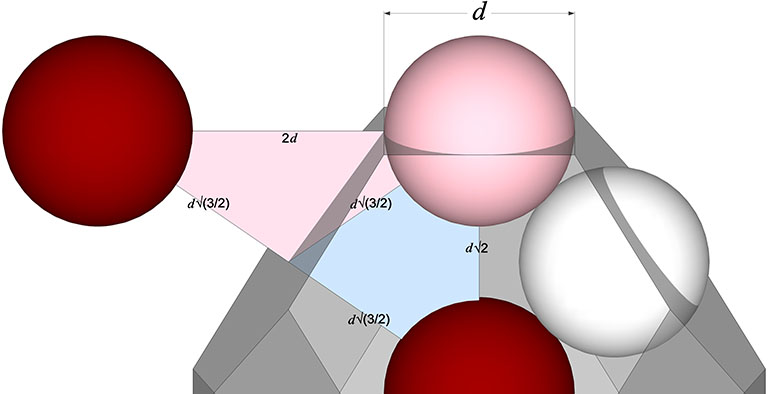
The Kelvin with the two isosceles triangles defined by its mid-sphere radii defining a right triangle with nuclei centered on each of its acute corners, and a non-unique nucleus centered on its right angle corner.
The corners of the right triangle formed from the midsphere radii coincide with the centers of nuclei in the isotropic vector matrix.

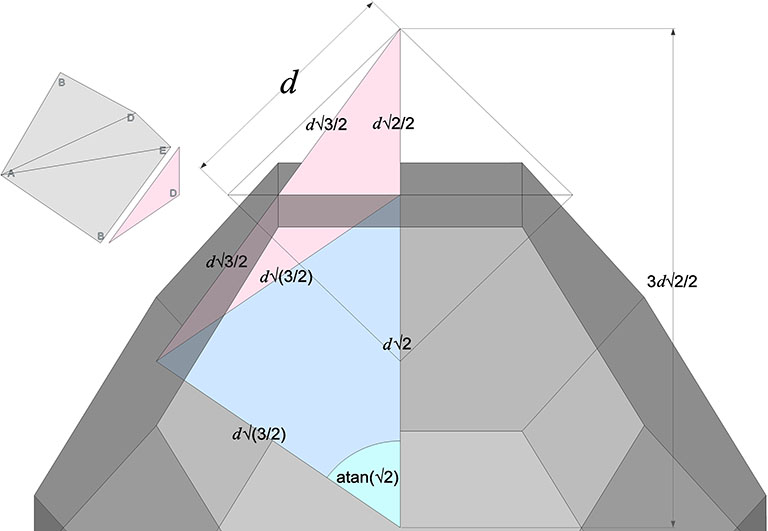
Extending the mid-square-face radius to a point where it crosses a line drawn perpendicular to the mid-hexagon-face radius creates a scalene triangle whose angles are curiously identical with the interior face of the B quanta module. Combining this scalene triangle with the isosceles triangle mentioned above creates a right triangle whose legs measure 2d√2/2 and d√(3/2). The mid-square-face radius extends d√2/2 beyond the face, exactly half of the face’s diagonal length, and half the mid-square-face radius. This suggests a rotational transformation of the Kelvin that may shadow the space-to-sphere, sphere-to-space transformations of the isotropic vector matrix, something begging to be investigated further, along with that curious appearance of the interior face of the B quanta module (pink in the illustration below).

The Kelvin with an isosceles triangle (blue) formed by the in-sphere radii which, together with a scalene triangle (pink) formed the chord between them, and the extension of the square-face-radius to where it crosses a perpendicular to the radius to mid-hexagon-face radius. Inset of an unfolded B quanta module (gray) with its matching scalene triangle set apart in pink.
Extending the mid-square-face radius to a point where it crosses the perpendicular to the mid-hexagon-face radius forms a scalene triangle exactly proportional to the interior face of the B quanta module (inset upper left).

If we replace the twelve vertices of a one-frequency Kelvin with spheres, we find that they occupy the spaces between the 42 spheres of the two 2-frequency vector equilibrium (VE) shell. The 2-frequency VE is significant because its shell is the last to fully enclose the nucleus without containing any new potential nuclei. The 1-frequency Kelvin complements the 2-frequency VE to fully isolate unique nuclear domains.

Spheres close-paced as a 1F Kelvin merging with spheres close packed as a 2F vector equilibrium.
The one-frequency Kelvin occupies the spaces between the spheres of the two-frequency VE and fully isolates the nucleus.

Kelvins with even frequencies (odd numbers of spheres to the side) are coincident with the radially close-packed spheres of the isotropic vector matrix. Those with odd frequencies (even numbers of spheres to the side) occupy the spaces between radially close-packed spheres.

Close packed spheres forming 1F, 2F, 3F and 4F Kelvins centered on vector equilibria each 1F higher emphasizing that odd-frequency Kelvins (1F and 3F) are shifted 1/2 a sphere diameter in relation to the even numbered Kelvins (2F and 4F).
Kelvins of even frequencies (white spheres) are coincident with the spheres of the isotropic vector matrix. Kelvins of odd frequencies (gray spheres) occupy the spaces between them.

At the center of odd Kelvins is a space, i.e., concave VE, and at the center of even Kelvins is a sphere. Note that the odd Kelvins in the above examples which fully isolate the nucleus have been shifted by 1/2 of a sphere diameter out of their natural position in the matrix. (See also: Spaces and Spheres (Redux), and; Spheres and Spaces.)

In the figures below, spheres and spaces are represented by the two quanta module constructions of the rhombic dodecahedron.

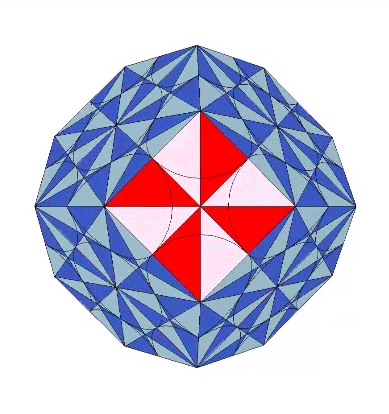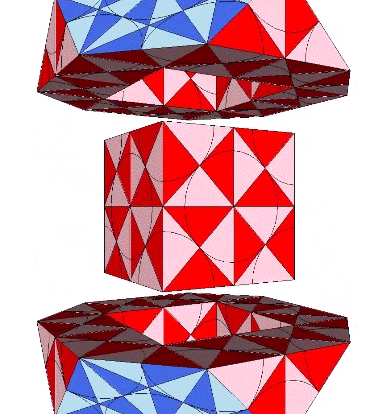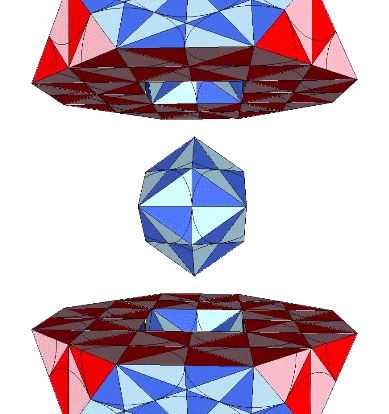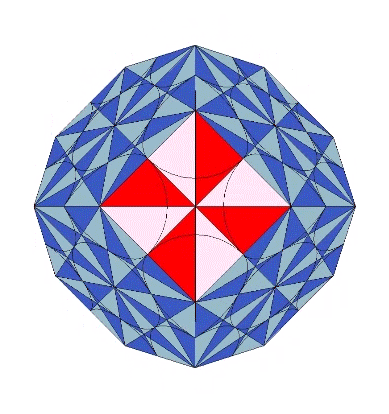
Quanta module construction of an F1 Kelvin opening up to reveal a 2F cube and a rhombic dodecahedron space at its center.
The one-frequency (F1) Kelvin, as with all odd-numbered Kelvins, has a space at its center.
An F2 Kelvin opening to reveal three nested vector equilibria and rhombic dodecahedron sphere at its center.
The two-frequency (F2) Kelvin, as with all even-numbered Kelvins, has a sphere at its center.

Fuller conceived the Kelvin as a truncated tetrahedron…

The edges and vertices of the regular tetrahedron (left) are truncated to construct the Kelvin, or truncated octahedron (right).
The six edges and four vertices of the regular tetrahedron (left) are truncated to create the Kelvin (right).

…and associated it with his Seven Axes of Symmetry.

Transparent Kelvin at the center of a transparent tetrahedron with the seven axes of symmetry.
Fuller used the Kelvin to illustrate his seven axes of symmetry which he derived from the truncations of the tetrahedron’s four vertices and six edges.

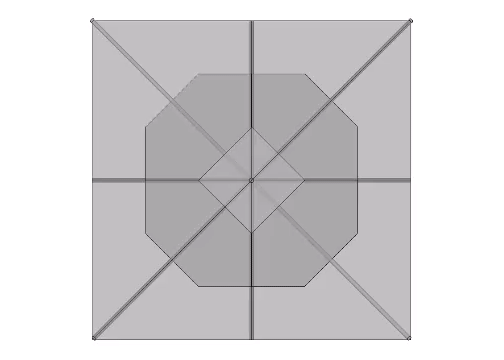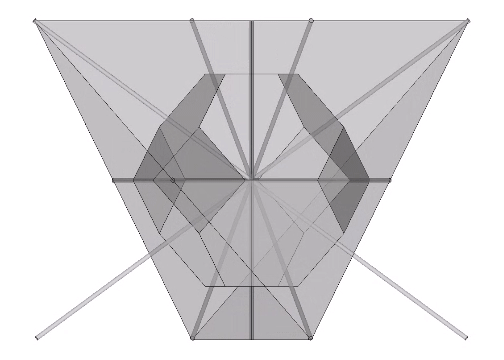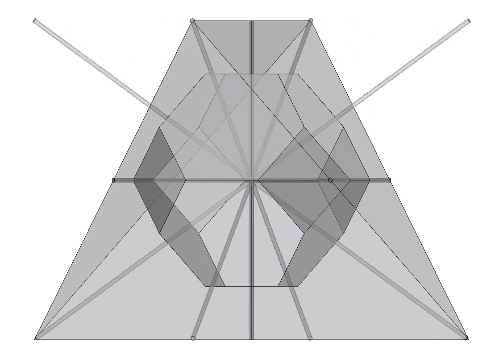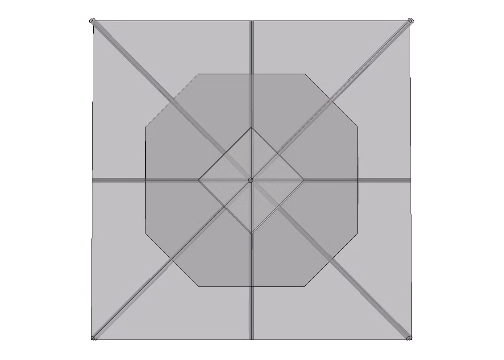
Fuller’s conception of the Kelvin as a truncated tetrahedron, rather than a truncated octahedron, is perhaps due to its association with the spherical form of the tensegrity tetrahedron, the six-strut tensegrity sphere or Jessen Orthogonal Icosahedron.

The Kelvin truncated octahedron (left) is used to construct the six-strut tensegrity sphere (middle) or Jessen Orthogonal icosahedron (right).
The six-strut tensegrity sphere (middle) is constructed by joining two-each vertices from opposing square faces of the Kelvin (left). The Jessen orthogonal icosahedron (right) describes its polyhedral shape.

Leave a comment