I’ve updated this topic with improved illustrations here: The 25 Great Circles of the VE (new illustrations).
The 25 great circles of the vector equilbrium (VE) disclose the following spherical polyhedra: the octahedra; the vector equilibrium (VE); the tetrahedron; the rhombic dodecahedron; and the cube.
Octahedron
The spherical octahedron is disclosed in the 3 great circles defined by the VE’s 3 square-face-to-face axes of spin. Each face contains 6 of the 48 LCD triangles.

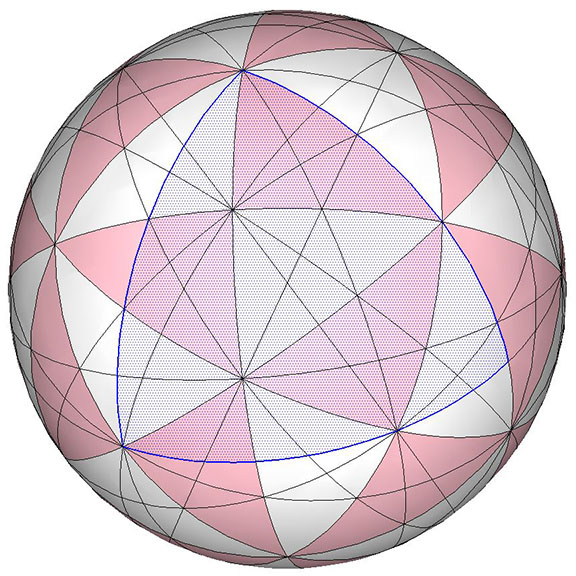
Vector Equilibrium (VE or Cuboctahedron)
The spherical VE is disclosed in the 4 great circles defined by the VE’s 4 triangular-face-to-face axes of spin. Both the triangular and the square face contain only partial LCD triangles.

Tetrahedron
The spherical tetrahedron, rhombic dodecahedron, and cube are disclosed in the 6 great circles of the VE’s 6 vertex-to-vertex axes of spin. Each face contains 12 of the 48 LCD triangles.

Rhombic Dodecahedron
Each face of the spherical rhombic dodecahedron contains 4 of the 48 LCD triangles.

Cube
Each face of the spherical cube contains 8 of the 48 LCD triangles.

Octahedron (alternate)
An alternate spherical octahedron is disclosed in the 12, 6, and 4 great circles defined by the VE’s 12 edge-to-edge, 6 vertex-to-vertex, and 4 triangular-face-to-face axes of spin. Each face contains 3 full, and 6 partial LCD triangles.