“The rhombic dodecahedra symmetrically fill allspace in symmetric consort with the isotropic vector matrix. Each rhombic dodecahedron defines exactly the unique and omnisimilar domain of every radiantly alternate vertex of the isotropic vector matrix as well as the unique and omnisimilar domains of each and every interior-exterior vertex of any aggregate of closest-packed, uniradius spheres whose respective centers will always be congruent with every radiantly alternate vertex of the isotropic vector matrix, with the corresponding set of alternate vertexes always occuring at all the intertangency points of the closest-packed spheres.”
—R. Buckminster Fuller, Synergetics, 426.20
The rhombic dodecahedron with unit long face diagonal, d:
- 12 rhomboid faces, 14 vertices, 24 edges
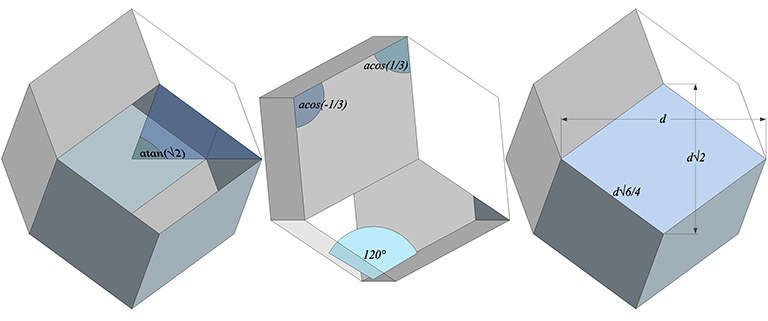
- Face Angles: atan(2√2) ≈ 109.471221°, and 2×atan(√2) ≈ 70.528779°
- Dihedral Angle: 120°
- Central Angle: atan(√2) ≈ 54.735610°
- Edge Length; d√6/4
- Volume (in tetrahedra): 6d³
- Volume (in cubes): d³2√2
- A quanta modules: 96
- B quanta modules: 48
- Surface area (in equilateral triangles) = d²×4√6
- Surface area (in squares): d²×3√2
- In-sphere radius: d/2
- Mid-sphere radius: d√3/3
- Circum-sphere radius (to vertices of long diagonal): d√2/2
- Circum-sphere radius (to vertices of short diagonal): d√6/4
The rhombic dodecahedron may be constructed from a single paper strip.
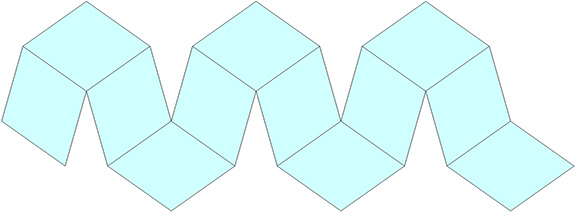
Eleven sequential folds of 60° each produce the the regular rhombic dodecahedron.
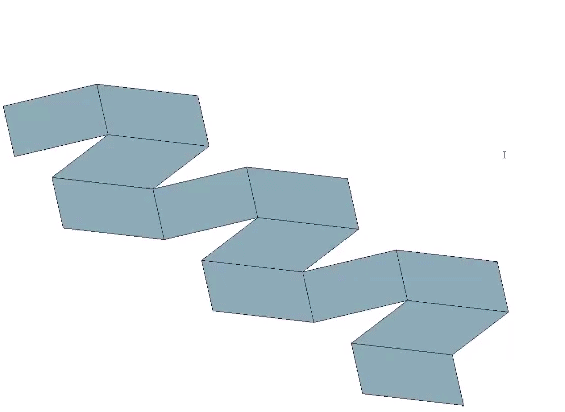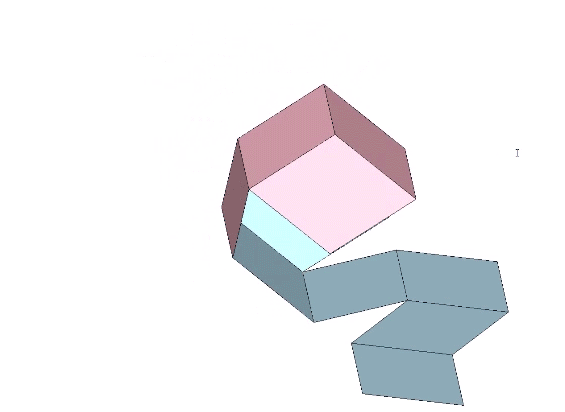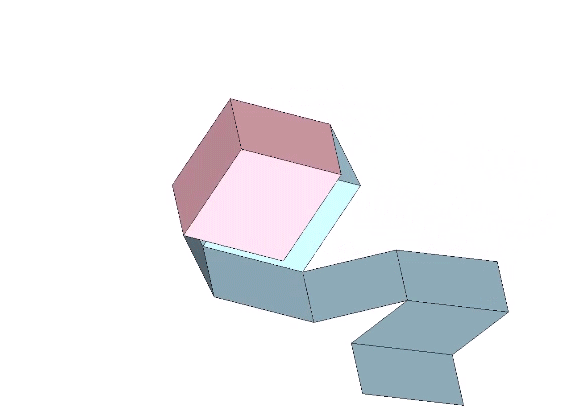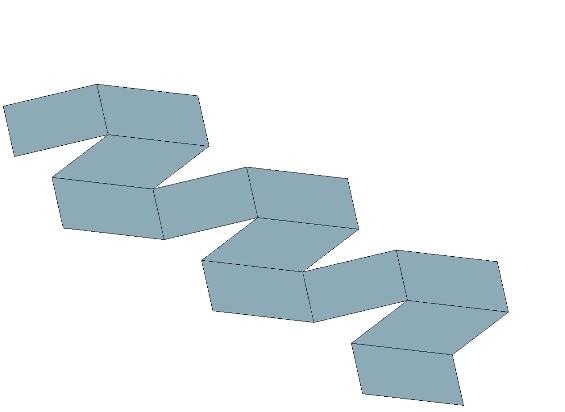
The in-sphere diameter describes a sphere that is fully enclosed by the rhombic dodecahedron, and is equal to the length of the long diagonal, d, of its rhomboid face. If d is taken to be unity, the tetrahedral volume of the rhombic dodecahedron is exactly 6, and defines the polyhedral domain of the radially close-packed spheres of the isotropic vector matrix.

The mid-sphere diameter defines the sphere whose radii intersect the edges of the rhombic dodecahedron at right angles. Its length is 2d√3/3.
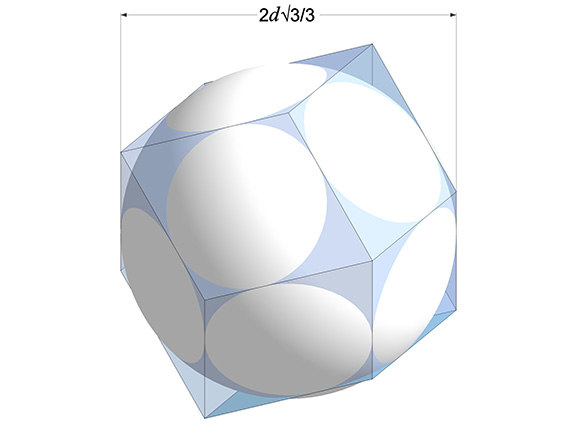
Note the mid-sphere radius does not intersect the edges at their mid-point, as might be expected. Rather, the intersect divides the edge length, a, into 1/3 and 2/3 segments, as illustrated below.

The circum-sphere diameter defines the sphere that fully encloses the rhombic dodecahedron. Its length is d√2. The radius, i.e., one half of the diameter, is identical with the length of the short diagonal, i.e., the shorter of the two widths of its rhomboid face: d√2/2.
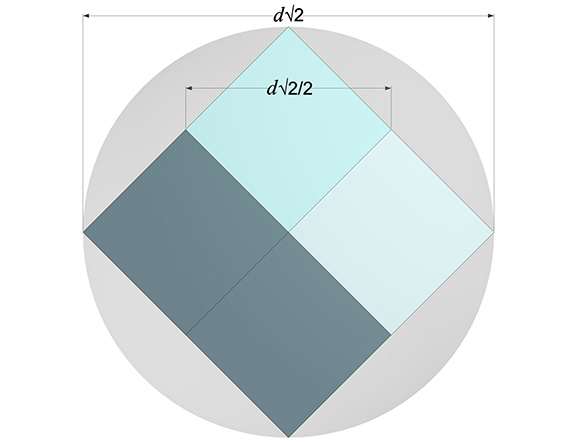
The circum-sphere radii intersect the rhombic dodecahedron at the vertices of its long diagonal, i.e., the longer dimension of its rhomboid face. The radius of the sphere that intersects the vertices of its short diagonal, i.e., the shorter dimension of its rhomboid face, is d√6/4, which, curiously, is identical with the edge length. The diameter of this sphere is, naturally, two times that length, or d√6/2.

Rhombic dodecahedra close pack to fill all space in exactly the same way that unit-radius spheres close pack around a central nucleus, as vector equilibria (VEs) of increasing frequency. That is, the polyhedral domain of each sphere in a cluster of radially close-packed spheres is a rhombic dodecahedron whose in-sphere radius is the radius of the sphere. (See Formation and Distribution of Nuclei in Radial Close-Packing of Spheres.)
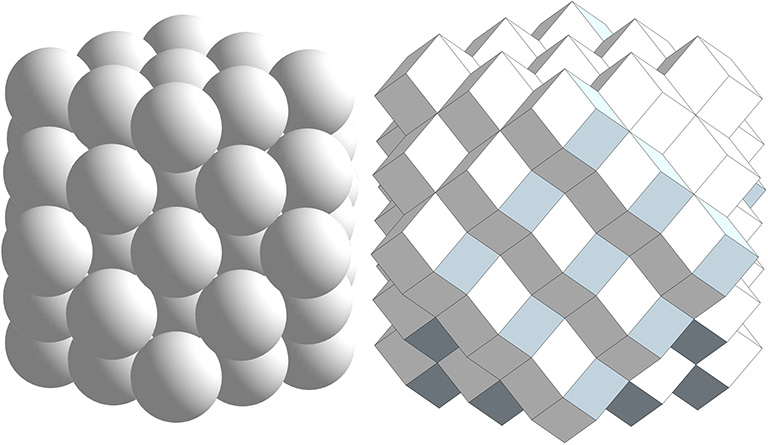
(Click on image to view animation in new tab.)
The rhombic dodecahedron can be constructed by adding quarter tetrahedra to each of the eight faces of a regular octahedron.

Alternatively, the rhombic dodecahedron can also be constructed by subdividing the cube into six identical pyramids whose apexes converge at its center of volume. These are then added to the faces of another cube, or simply rotated 180° to expose their internal faces. The construction can also be thought of as turning the cube inside out.
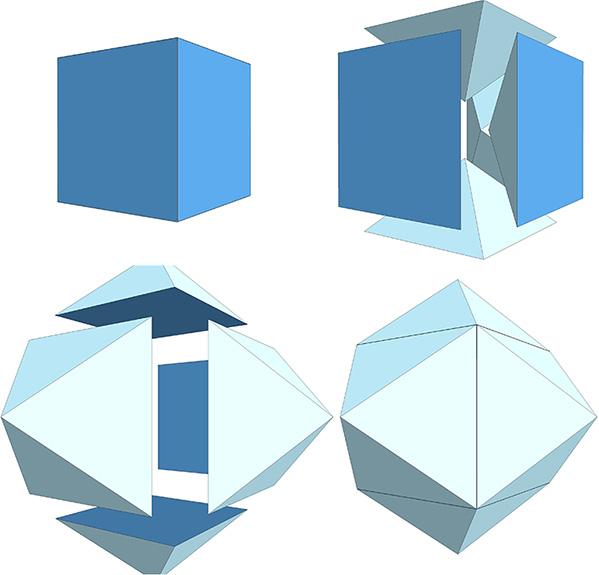
(Click on image to view animation in new tab.)
The long and short diagonals of the rhomboid faces define a regular octahedron and cube respectively. The ratio of the long diagonal over the short diagonal is exactly √2.

The lines along which the the cube and the octahedron intersect are equal to the in-sphere radius of the rhombic dodecahedron and describe vector equilibrium (VE).

This relationship is also disclosed in the great circles in The 25 Great Circles of the Vector Equilibrium (VE). The set of six great circles described by the the axes connecting opposite vertices of the VE disclose the spherical rhombic dodecahedron, as well as the spherical cube and the spherical tetrahedron (both positive and negative). See Vector Equilibrium: Spherical Polyhedra Described by Great Circles and The 25 Great Circles of the VE (new illustrations).
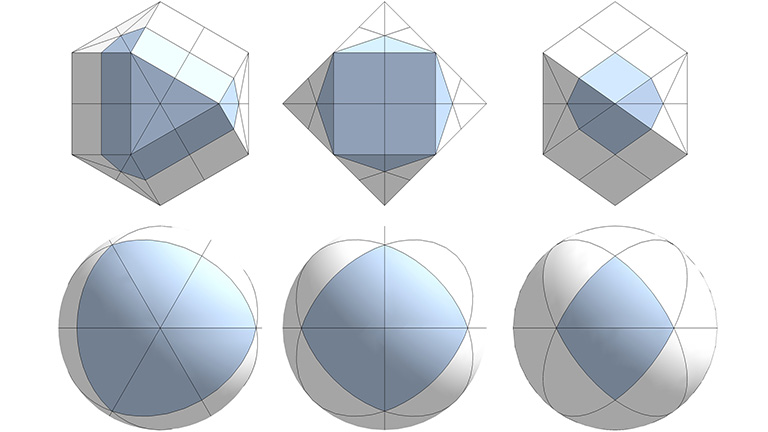
All the great circle sets may be modeled as disks which can then be folded into “bow ties” along their lines of intersection and reassembled. The bow-tie model of the set six great circles of the VE is illustrated below. For more information, see Great Circle Bow-Ties of the VE.

The vertices of the rhombic dodecahedron correspond to the distribution of unique nuclei in the isotropic vector matrix.
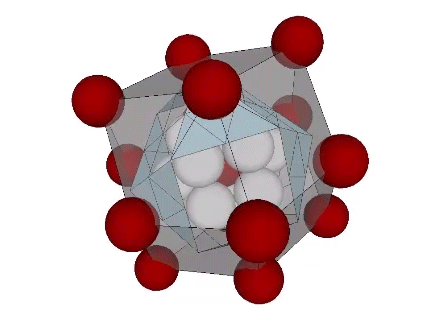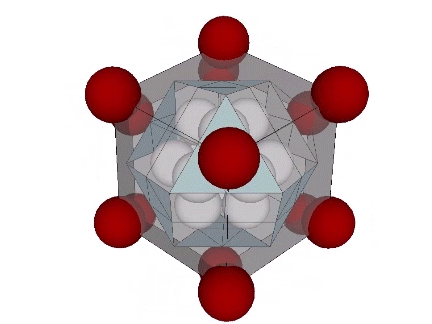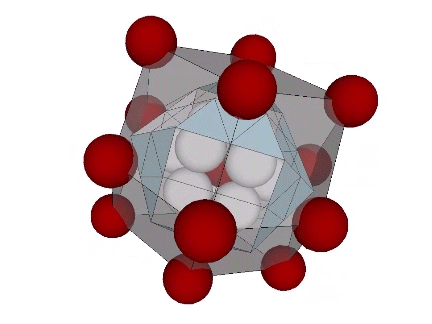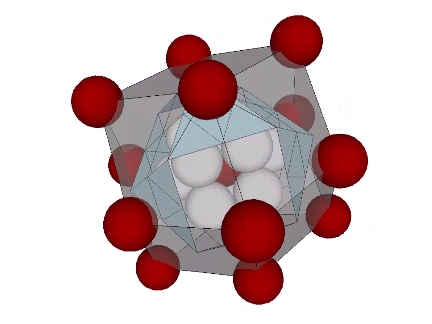
This distribution is also seen in the Kelvin and Weaire-Phalen matrices of unit-volume cells. For more information, see: Formation of New Nuclei in Close Packing of Spheres; The Kelvin Truncated Octahedron; and Tetrakaidecahedron and Pyritohedron.
In the quantum model of the isotropic vector matrix (see A and B Quanta Modules) there are two different constructions of the rhombic dodecahedron—one occupying the position of the spheres, and the other occupying the position of the spaces (concave VEs) between the spheres.

The one identified with the sphere has all of its constituent quanta modules exposed on the surface, a construction which conveys energy dispersal, or radial pressure:

The one identified with the spaces between the spheres is the outside-in version of the sphere. Its energy-dispersing B quanta modules are fully contained inside a wrapper of energy-conserving A quanta modules, conveying energy-conserving circumferential tension:

The two exchange places (one transforms into the other) during the jitterbug transformation. See also: Quanta Module Constructions of the Rhombic Dodecahedron; Spheres and Spaces; and Anatomy of a Sphere.