Minimum All-Space-Filling Tetrahedron: “MITE”

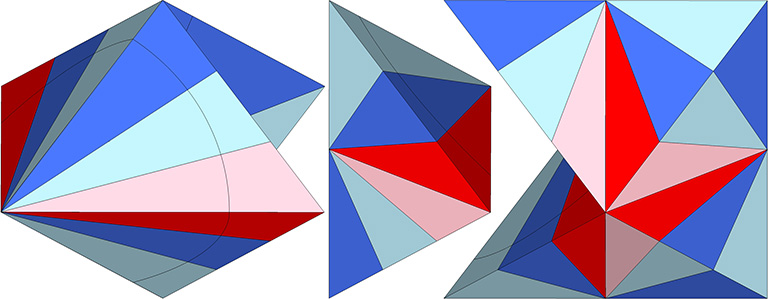
“Of all the all-space-filling module components, the simplest are the three-quanta-module Mites, consisting of two A Quanta Modules (one A positive and one A negative) and of one B Quanta Module (which may be either positive or negative). Thus a Mite can be positive or negative, depending on the sign of its B Quanta Module. The Mites are not only themselves tetrahedra (the minimum-sided polyhedra), but they are also the simplest minimum-limit case of all-space-filling polyhedra of Universe, since they consist of two energy-conserving A Quanta Modules and one equi-volume energy-dispersing B Quanta Module. The energy conservation of the A Quanta Module is provided geometrically by its tetrahedral form: four different right-triangled facets being all foldable from one unique flat-out whole triangle, which triangle’s boundary edges have reflective properties that bounce around internally to those triangles to produce similar smaller triangles: Ergo, the A Quanta Module acts as a local energy holder. The B Quanta Module is not foldable out of one whole triangle, and energies bouncing around within it tend to escape. The B Quanta Module acts as a local energy dispenser.”
—R. Buckminster Fuller, Synergetics, 986.421

“We then discover that the Mite, with its two energy-conserving A Quanta Modules and its one energy-dispersing B Quanta Module (for a total combined volume of three quanta modules), serves as the cosmic minimum allspace-filler, corresponding elegantly (in all ways) with the minimum-limit case behaviors of the nuclear physics’ quarks. The quarks are the smallest discovered “particles”; they always occur in groups of three, two of which hold their energy and one of which disperses energy. This quite clearly identifies the quarks with the quanta module of which all the synergetics hierarchy of nuclear concentric symmetric polyhedra are co-occurrent.”
—ibid., 986.454

The minimum all-space filling tetrahedron, or “Mite,” is formed from one negative and one positive A quanta module, plus either one positive or one negative B quanta module. (See A and B Quanta Modules.) As with all quanta modules, the mite comes in pairs, one positive and one negative.

Two A quanta modules and one B quanta module combine into a positive mite, then separate, turn themselves inside out, and recombine into a negative mite. — *The minimum space-filling tetrahedon, or “Mite” consists of a positive and negative A quanta module, and one positive or negative B quanta module.*

The Mite is an irregular tetrahedron that unfolds symmetrically to form a rectangle surmounted by an isosceles right triangle. From the mite’s isosceles triangular base, two sides unfold to form a rectangle with the base. The remaining side is an isosceles right triangle. The internal angles of the unfolded mite are: atan(√2/2) ≈ 35.264390°; atan(√2) ≈ 54.765610°, and; atan(2√2) ≈ 70.528779°.

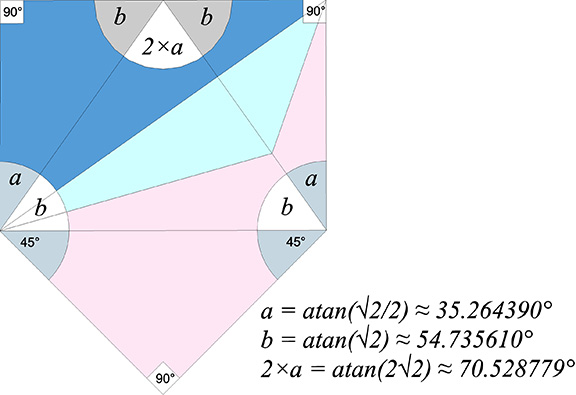
A polyhedron net of the mite, a rectangle surmounted by a right triangle, with angles indicated. — *Angular dimensions of the minimum all-space filling tetrahedron, or “Mite”, unfolded.*

In the section of Synergetics where Fuller introduces the Mite, he adds, in the third edition, the following to Figure 953.10 without comment:

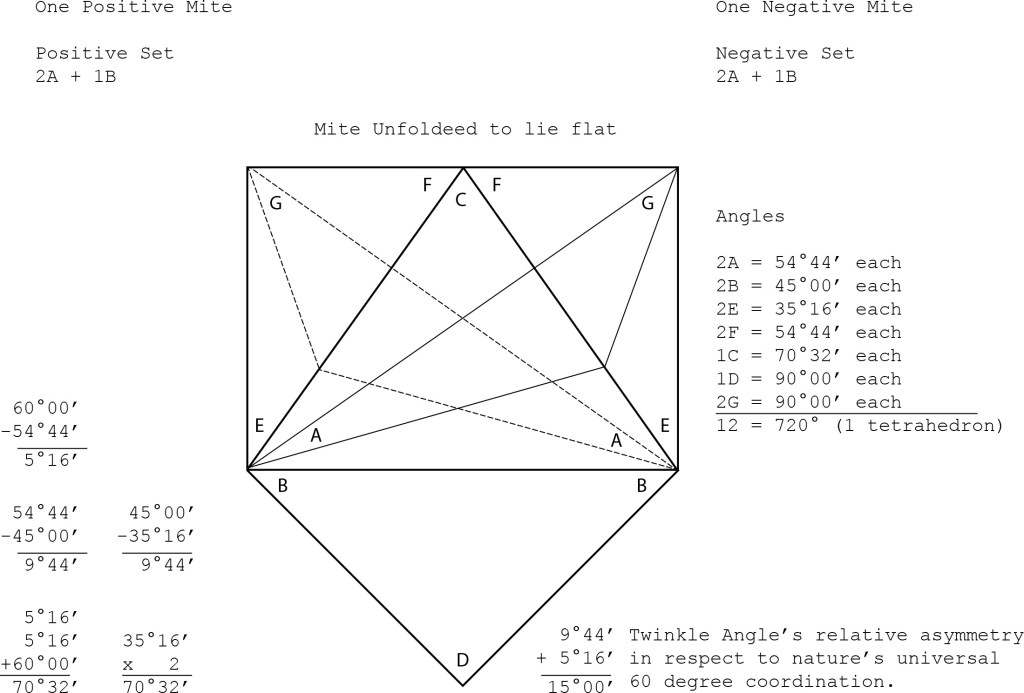
The mite positive and negative mite diagrammed as a polyhedron net, with calculations showing the relationship of its angles to the "twinkle angle." — *Figure 953.10 from the third edition of Synergetics, relating the “Twinkle Angle” to the Mite.*

The “Twinkle Angle” (≈ 5.26439°) is the amount shy of 90° in the largest angle of the unfolded A quanta module which otherwise bears striking resemblance to the right-angled Basic Disequilibrium LCD Triangle. The Mite beautifully resolves the Twinkle Angle’s asymmetry into right angles, and these calculations provide some insight into how it is done. The Mite’s internal angle of arctan(√2) is one Twinkle Angle shy of 60°:

60° – 54.735610° = 5.26439°.

The Mite’s internal angle of arctan(2√2), is two Twinkle Angles greater than 60°:

60° + (2×5.26439°) = 70.52878°

The difference between the Mite’s two internal angles, arctan(√2) and 45°, and the difference between 45° and the Mite’s last remaining non-90° angle, arctan(√2/2), is approximately 9.73561° which when added to the Twinkle Angle equals exactly 15°:

5.26439° + 9.73561° = 15°

Fuller believed such subtle asymmetries as this were a signal of identities between phenomena otherwise hidden by phase changes:

“Probability of Equimagnitude Phases: The 6° spherical excess of the Basic Disequilibrium 120 LCD Triangle, the 5° 16′ “twinkle angle” of the A quanta module triangle, and the 7° 20′ “unzipping angle” of birth, as in the DNA tetrahelix, together may in time disclose many equimagnitude phases occurring between complementary intertransforming structures.”
—Synergetics, 915.20

Fuller identified his quanta modules with the quarks which in particle physics constitute the fundamental units of matter. Quarks, like Mites, always come in sets of three. A proton, for example, consists of two “Up” quarks and one “Down” quark, while a Mite consists of two A quanta modules and one B quanta module.

The Couplers

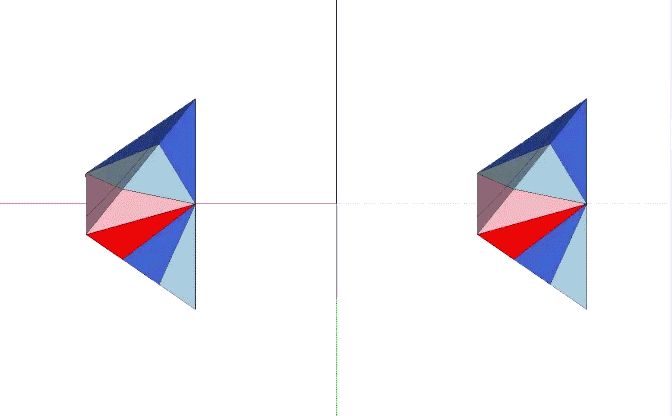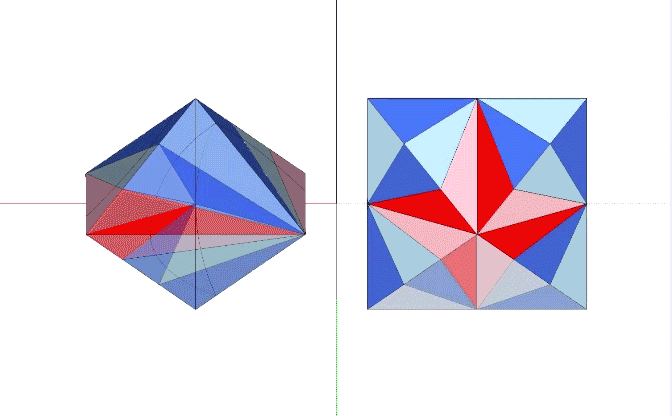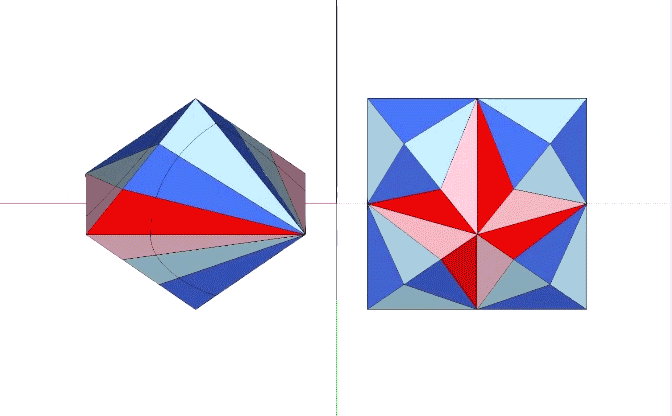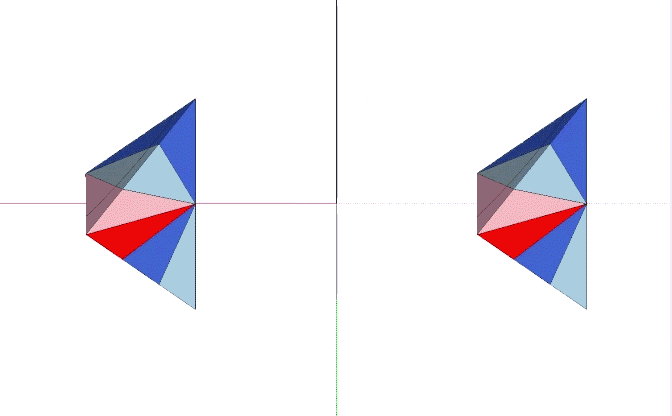
Eight Mites (four positive and four negative) combine to form either the Coupler, or the 1/6th rhombic dodecahedron. Each is a shallow octahedron with dimensions identical to the other—their only difference being in the orientation of their constituent Mites. The Coupler joins rhombic dodecahedra, and the 1/6th rhombic dodecahedra combine to form either of two rhombic dodecahedra—one representing the sphere and the other representing the space between spheres in the quanta model of the isotropic vector matrix.

The 1/6th rhombic dodecahedron arranges the the long edges of eight mites around its single short axis. This forms a shallow octahedron consisting of 24 quanta modules (1 tetra volume) with 16 A and 8 B quanta modules.

One sixth rhombic dodecahedron is constructed of eight Mites with their long edges arranged around its single short axis. — The 1/6th rhombic dodecahedron is a shallow octahedron constructed from eight Mites, four positive and four negative. The Mites’ long edges are arranged around the shallow octahedron’s single short axis.

Six 1/6th rhombic dodecahedra combine to form the two rhombic dodecahedra which always and only coexist in the quanta model of the isotropic vector matrix—one enclosing the space between spheres and the other enclosing the spheres themselves. (See Quanta Module Constructions of the Rhombic Dodecahedron.) The transformation of one to the other is accomplished by rotating the 1/6th rhombic dodecahedra 180°, essentially turning the rhombic dodecahedron inside out.

Two constructions of the rhombic dodecahedron transforming from one into the other by the 180° rotation of each of its one-sixth rhombic dodecahedra. — *One rhombic dodecahedron can be transformed into the other by rotating its six 1/6th rhombic dodecahedra 180°.*

When combined to fill all-space in the isotropic vector matrix, the 1/6th rhombic dodecahedron’s short axis connects the two distinct rhombic dodecahedra, i.e., spheres with spaces.

The Coupler, identified by Fuller, orients the short edges of the eight mites around the its single short axis.

The Coupler constructed of eight Mites with their short edges arranged around its single short axis. — Fuller’s “Coupler” (top) is a shallow octahedron identical to the 1/6th rhombic dodecahedron, but with its eight mites arranged so that their long edges form an equator around shallow octahedron’s single short axis.

When combined to fill all-space in the isotropic vector matrix, the two long axes of Fuller’s Coupler connect like-with-like rhombic dodecahedra, i.e. spheres with spheres, and spaces with spaces, their connections running perpendicular to each other.

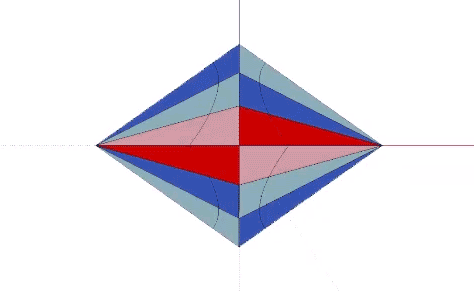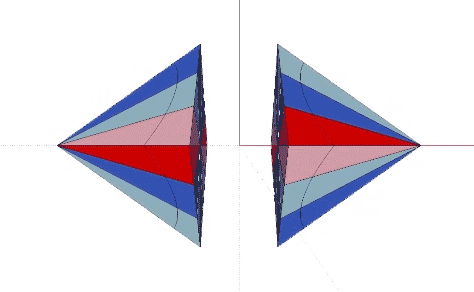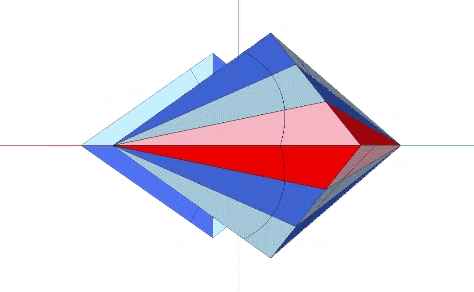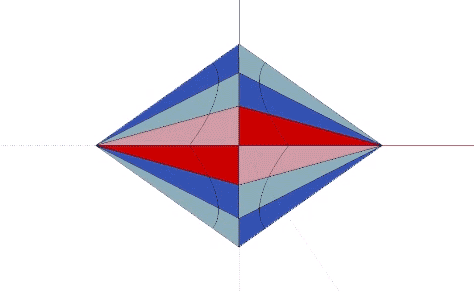
The Coupler bisected to reveal one of two faces of two constructions of the rhombic dodecahedron. — *The two bisections of the Coupler present two faces, those of the two rhombic dodecahedron representing spheres and spaces.*

Fuller’s Coupler actually connects four, not two rhombic dodecahedra, two representing spheres, and two representing spaces in the isotropic vector matrix.