Isotropic Vector Matrix as Transverse Waves

Greg Frederick

A tetrahedron may be constructed from two open-ended triangles.

Two equilateral triangles with one open vertex and the ends separated by the edge length. One clockwise plus one counter-clockwise triangle equals one regular tetrahedron.
Tetrahedron Constructed from Two Open-Ended Triangles

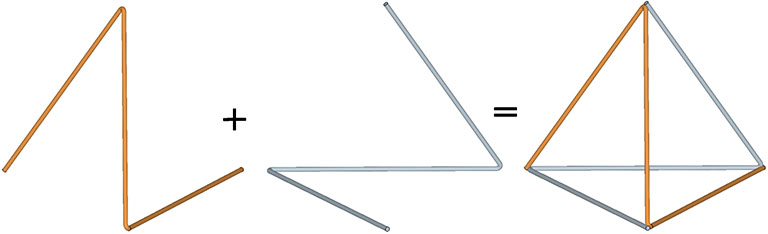
If we use this construction in the isotropic vector matrix, the open ends of each triangle join with similar triangles in the adjacent tetrahedra to form wave patterns that propagate linearly through the matrix, each oriented at 90° to the other. The entire matrix may be built though the duplication of orthogonally paired waves.

The open ends of equilateral triangles join with similar triangles to form wave patterns that propagate linearly through the matrix. Clockwise and counter-clockwise waves meet at right angles forming a regular tetrahedron at their intersection.
Transverse Waves in the Isotropic Vector Matrix

Significant to this model of the isotropic vector matrix is its demonstration of the fundamental principle that no two vectors may pass through the same point simultaneously. All vertices in the matrix redirect their vectors, rather than act as focal points for their convergence.

Detail of a vertex in the transverse wave model of the isotropic vector matrix showing that all vectors deflect from one another rather than merge at the vertices.
Deflecting Vectors at Vertices of the Transverse Wave Model of the Isotropic Vector Matrix

For each of the six axes of the isotropic vector matrix, i.e., the six vertex-to-vertex axes of spin of the vector equilibrium, there are four unique waves, two running clockwise and two running counter clockwise on either side of the axis, for a total of 24 (6×4) waves converging on and deflecting from every point.

Four chains of open-ended equilateral triangles running along a neutral axis through the sphere center, Two positive on top of the axis, and two negative below the axis, each constituting one clockwise and one counter-clockwise linear wave.
For each of the six axes of the isotropic vector matrix, i.e., the six vertex-to-vertex axes of spin of the vector equilibrium, there are four unique waves, two running clockwise and two running counter clockwise on either side of the axis.

Note that the axis that defines the linear orientation of the wave is excluded from the wave itself which traces a path along three of the remaining five edge vectors of the tetrahedron. The clockwise and counter-clockwise waves of the positive and negative tetrahedra each share one leg oriented at 90° to the wave’s directional axis, underscoring the polarization of the pair.

The six axes of the isotropic vector matrix define the six edges of the tetrahedron. The waves from these six axes wrap around each tetrahedron such that each of its six edges includes a leg from four separate waves.

The neutral axes of six chains of open-ended equilateral triangles aligned with the edges of a regular tetrahedron defined by their intersection. Legs from four of the six waves pass through each of the tetrahedron's six edges.
The neutral axes of six chains of open-ended equilateral triangles intersect to form a regular tetrahedron with four vectors per edge.

This recapitulates the quadrivalent (four vectors per edge) tetrahedron that results when the jitterbug is given an extra 180° twist.

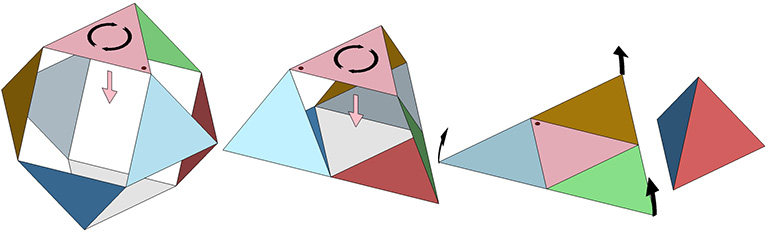
A vector equilibrium constructed from eight vertex-bonded triangular panels (left). The top triangle is given a 60° clockwise twist (left center) to form a top-truncated tetrahedron. An additional 60° twist flattens the four top faces against the four bottom faces (right center) which is then folded into the regular tetrahedron (right).
With a 180° twist, the jitterbugging VE can be collapsed into a regular tetrahedron with four vectors per edge.

This wave pattern can also be modeled with continuous ribbons of equilateral triangles which are then folded at the same angles as the three vectors of the open-ended triangle above.

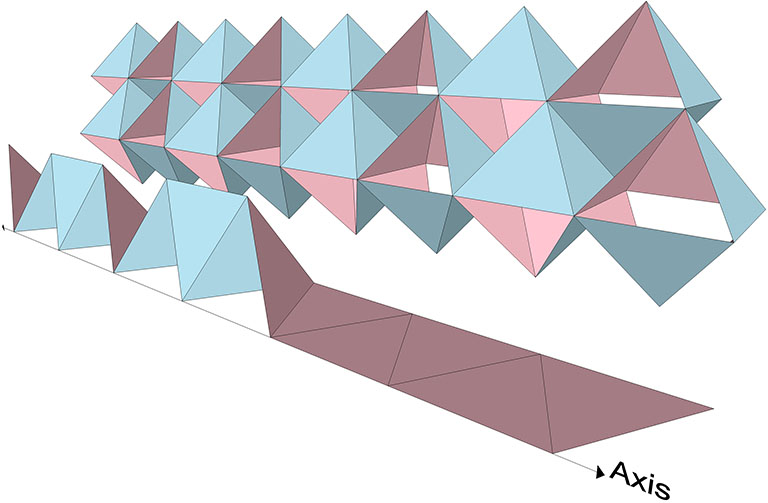
The isotropic matrix modeled by the folding of a linear ribbon of equilateral triangles mirrors the transverse wave model of open-ended triangles.

The octahedron can be constructed from four open-ended triangles.

Four open-ended equilateral triangles combine to form the regular octahedron.

The open-ended triangles of the octahedron may be joined in parallel linear waves that form a continuous chain of octahedra.

The open-ended triangles of the octahedron joined in four parallel linear waves forming a continuous chain of octahedra.
The open-ended triangles of the octahedron joined in four parallel linear waves forming a continuous chain of octahedra.

The icosahedron can be constructed from ten open-ended triangles.

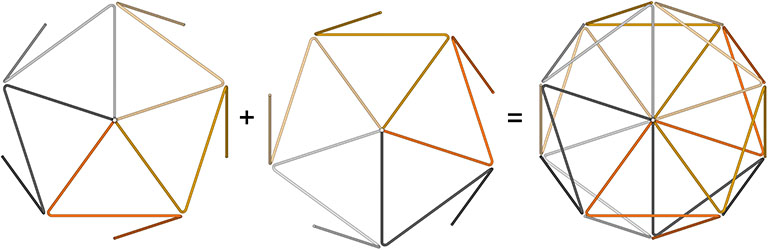
Two groups of five open-ended triangles radiating from a common vertex combine to form the twenty triangular faces of the regular icosahedron.
Ten open-ended equilateral triangles combine to form the regular icosahedron.

There are numerous ways of joining the open-ended triangles of the icosahedron end-to-end, but all form wave-dispersal patterns in which the icosahedron appears never to repeat.

Open-ended triangles of the regular icosahedron joined end-to-end and radiating away from the central icosahedron.
Joining the open-ended triangles of the regular icosahedron forms a wave-dispersal pattern that appears to never repeat the original icosahedron.

Leave a comment