The Geometry of Thinking

“The tetrakaidecahedron develops from a progression of closest-sphere-packing symmetric morphations at the exact maximum limit of one nuclear sphere center’s unique influence, just before another nuclear center develops an equal magnitude inventory of originally unique local behaviors to that of the earliest nuclear agglomeration.“
— R. Buckminster Fuller, Synergetics, section 942.71

Note: For instructions on how to construct the Weaire-Phelan structure, see my post, Construction Method for the Pyritohedron and Tetrakaidecahedron of the Weaire-Phelan Structure.

The tetrakaidecahedron that Buckminster Fuller had in mind, and which he refers to as “Lord Kelvin’s Solid” was the truncated octahedron, a polyhedron which, like the vector equilibrium (VE), has fourteen sides, and which at the time (1975) was considered the tentative solution to the Kelvin Problem: How can space be partitioned into cells of equal volume with the least area of surface between them? Fuller, like most others, assumed that a bitruncated cubic honeycomb consisting of truncated octahedron cells was, with only slight deformation, the most likely solution. Ten years after Fuller’s death, in 1993, Denis Weaire of Trinity College Dublin and his student Robert Phelan showed through computer simulations of foam that a combination of pyritohedra and tetrakaidecahedra of equal volume could fill space more efficiently, with a surface area to volume ratio 0.3% less that that of Kelvin’s truncated octahedra.

There is a curious correlation between the close packing of unit-radius spheres and foams of unit-volume cells. Spheres close pack around a central sphere as vector equilibria of increasing frequency. The polyhedral domain of each sphere is a rhombic dodecahedron. Rhombic dodecahedra close pack exactly as spheres close pack, twelve around one. (See The Rhombic Dodecahedron.) If we partition close-packed spheres into nuclear domains of central spheres surrounded by unique 12-sphere shells, the shells are distributed as Kelvin’s tetrakaidecahedra, but the nuclei themselves are distributed exactly as the pyritohedra are distributed in the Weaire-Phelan matrix. See: Formation of New Nuclei in Close-Packing of Spheres.

Both the bitruncated cubic honeycomb consisting of truncated octahedra, and the Weaire-Phelan matrix consisting of pyritohedra and tetrakaidecahedra, isolate unique nuclei in the close-packed spheres of the isotropic vector matrix. In the figure below, the isolated nuclei are shown as red spheres, and those that share their shells with neighboring nuclei are shown as pink spheres. In the top row, the vector equilibria of the isotropic vector matrix surround both the red and pink nuclei; they do not distinguish unique nuclei. The truncated octahedra in the middle row do distinguish unique nuclei if their edge length is equal to the sphere diameter, with every other nuclear domain sharing a common center with a truncated octahedron. The Weaire-Phelan matrix (bottom row) distinguishes unique nuclei by their own polyhedron, the pyritohedron, while those that share their shells with neighboring nuclei are centered between positive and negative tetrakaidecahedra. The tetrakaidecahedra are sized so that their circumsphere radius is equal the the sphere diameter.

The pyritohedron is familiar as its namesake, the pyrite crystal, or “fool’s gold,” which like the regular dodecahedron has twelve identical faces. The pentagonal faces of the pyritohedron are irregular, with one edge slightly longer that the other four. The pyritohedron can be derived from the Jessen Orthogonal Icosahedron, more familiar in Fuller’s geometry as the convex shape of the six-strut tensegrity sphere. The correlation is intriguing. See also: Tensegrity, and Icosahedron Phases of the Jitterbug.

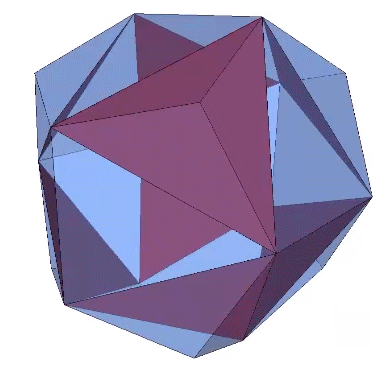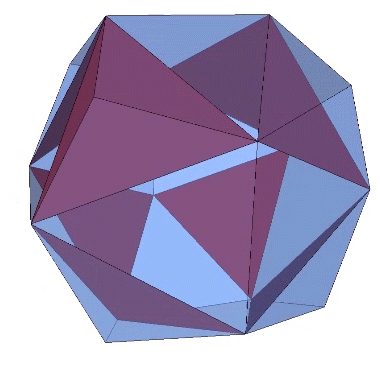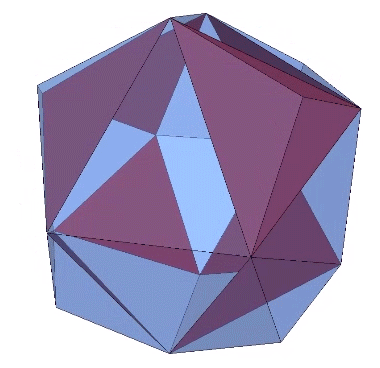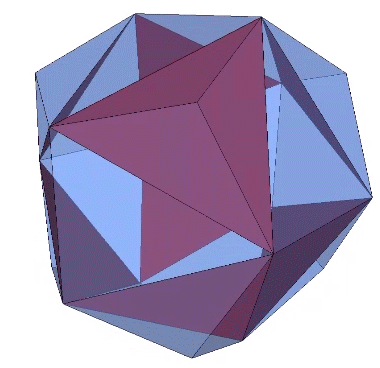
The pyritohedron can be constructed by the addition of eight shallow tetrahedra to each of the eight equilateral triangles of the Jessen icosahedron. The height of these tetrahedra is exactly 1/3 the in-sphere radius of the Jessen icosahedron, or one quarter the circumsphere radius of the pyritohedron.

An even more beautiful symmetry, I think, is disclosed by connecting the peaks of the eight shallow tetrahedra to form a cube.

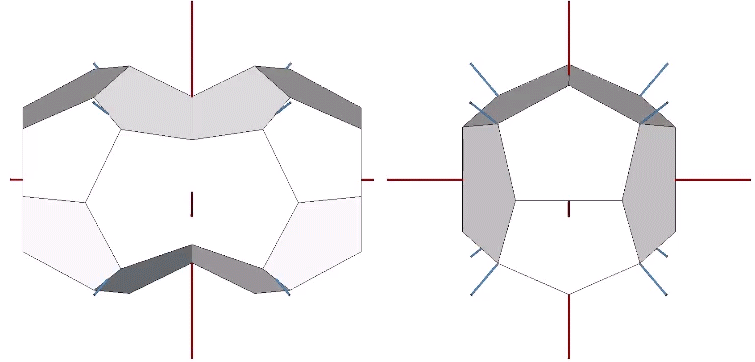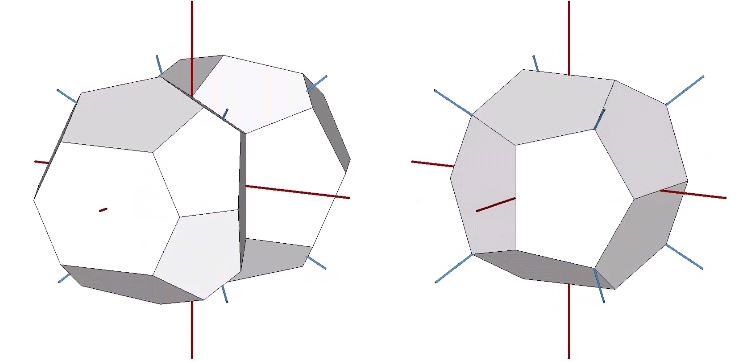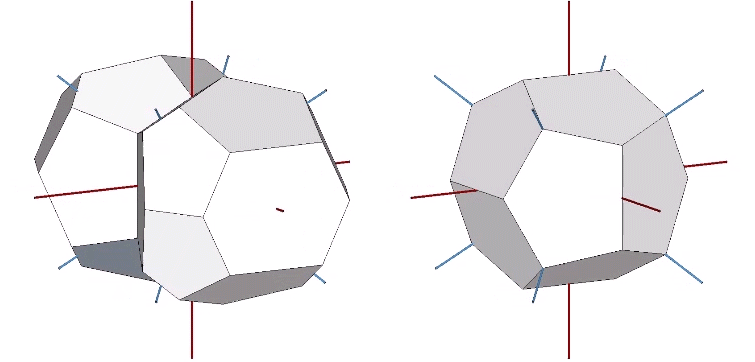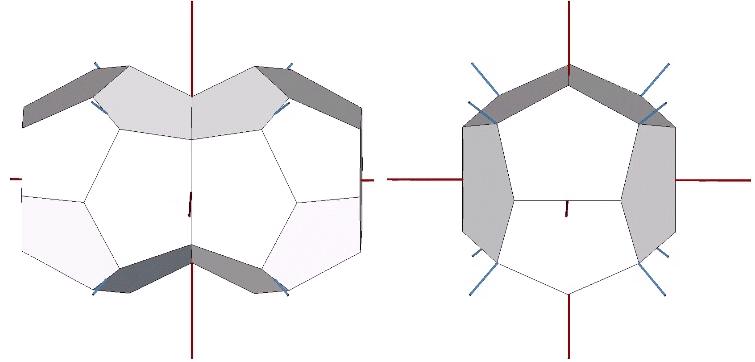
The tetrakaidecahedron that combines with the pyritohedron to fill all space is a 14-sided polyhedron consisting of two elongated hexagonal faces and two sets of pentagonal faces: four matching the faces of the pyritohedron, and eight elongated pentagons.

Lines drawn from the base to peak of the eight elongated pentagon faces, and from the line’s endpoints to the center of the tetrakaidecahedron, form equilateral triangles whose edge lengths in the Weaire-Phelan matrix correspond to the diameter of the nuclear spheres isolated by the pyritohedra.

The appearance of eight equilateral triangles in both the pyritohedron and the tetrakaidecahedron suggests the possibility of a jitterbug-like transformation from one to the other. Their edge lengths, however, differ. The edge length of the eight equilateral triangles in the pyritohedron is approximately 1.091135 times the edge length of those in the tetrakaidecahedron.

Connecting the unit-length radials of adjacent tetrakaidecahedra forms shells around the nuclei in the shape of Kelvin’s truncated octahedron.

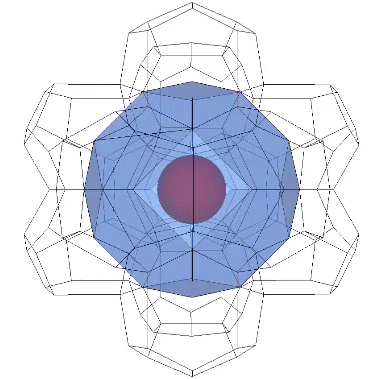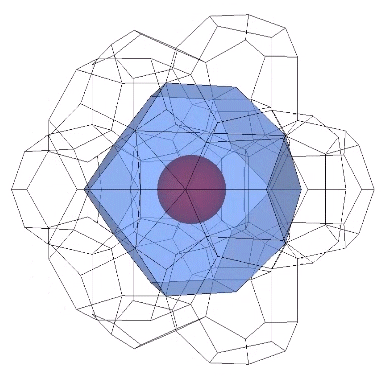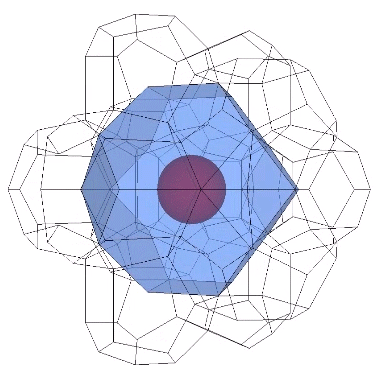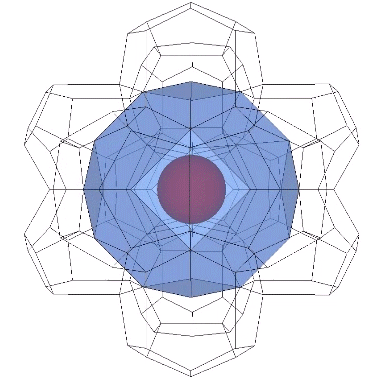
If we align the unit vectors of the Weaire-Phelan matrix with the isotropic vector matrix, the pyritohedra enclose spaces rather than spheres. If we align them with the distribution of nuclei, the Weaire-Phelan matrix is 180° out of phase with the isotropic vector matrix. This phase difference suggests an energetic relationship between the two matrices that may provide insight into the jitterbug transformation, and its oscillations between spheres and spaces.

The pyritohedron, and the tetrakaidecahedra paired with its mirror image, both align with the The Seven Axes of Symmetry.