Tetrahelix

Greg Frederick

“These helical columns of tetrahedra, which we call the tetrahelix, explain the structuring of DNA models of the control of the fundamental patterning of nature’s biological structuring as contained within the virus nucleus. It takes just 10 triple-bonded tetrahedra to make a helix cycle, which is a molecular compounding characteristic also of the Watson-Crick model of the DNA. When we address two or more positive (or two or more negative) tetrahelices together, they nestle their angling forms into one another. When so nestled the tetrahedra are grouped in local clusters of five tetrahedra around a transverse axis in the tetrahelix nestling columns. Because the dihedral angles of five tetrahedra are 7° 20′ short of 360°, this 7° 20′ is sprung-closed by the helix structure’s spring contraction. This backed-up spring tries constantly to unzip one nestling tetrahedron from the other, or others, of which it is a true replica. These are direct (theoretical) explanations of otherwise as yet unexplained behavior of the DNA.”
—R. Buckminster Fuller, Synergetics, caption to fig. 933.01

Regular tetrahedra do not combine to fill all space. They can however be face-bonded to form a helical structure Fuller called the “tetrahelix.”

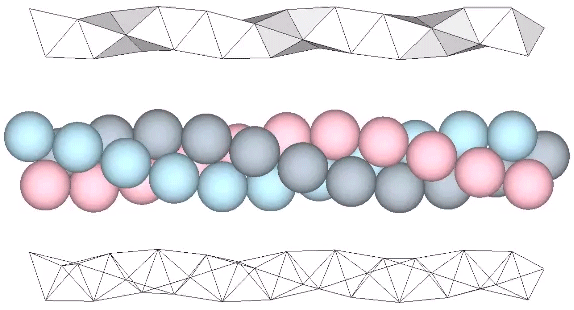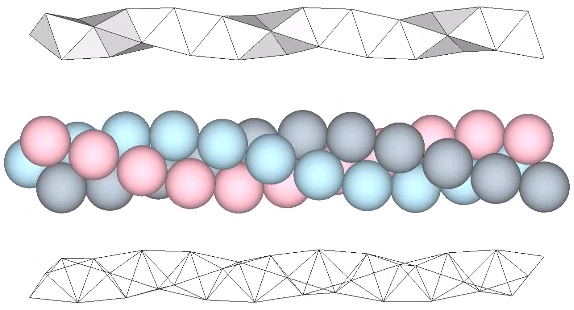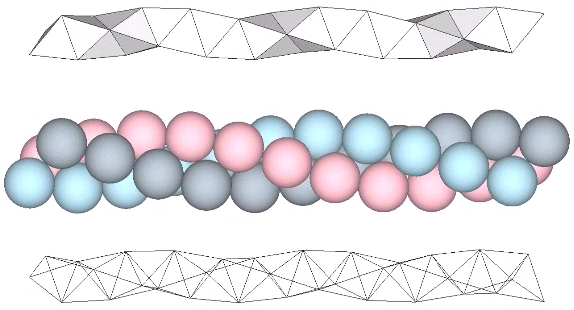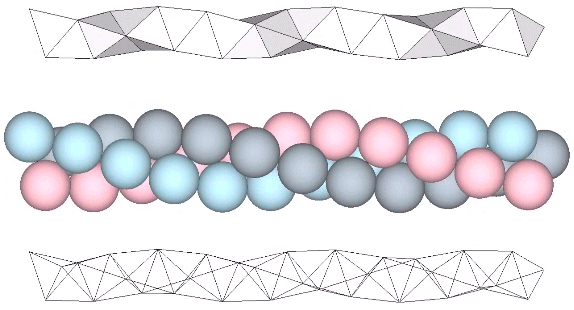
Tetrahelix represented as polyhedra (top); spheres (middle); and as a wireframe model (bottom).
Three constructions of the tetrahelix: a double helix of regular tetrahedra (top); a triple helix of close packed unit spheres (middle); and a wireframe model exposing its complete structure (bottom)

The tetrahelix can be constructed as a single, double, or triple helix, oriented either clockwise or counter-clockwise. The single helix completes about 10 cycles per 30 tetrahedra; the double helix completes about 5, and the triple helix completes about 1 cycle per 30 tetrahedra.

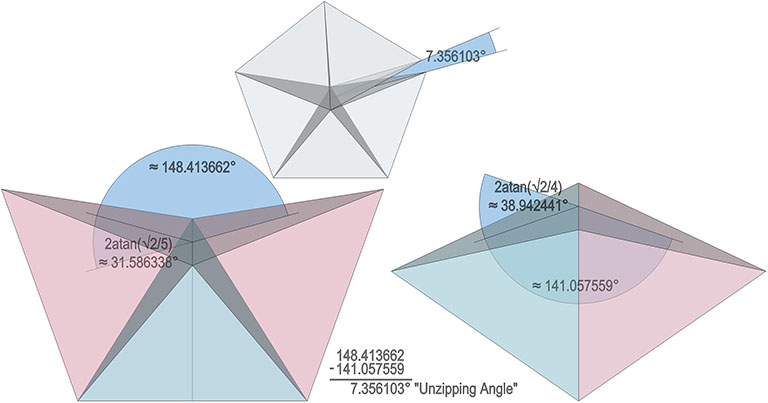
The single helix is folded from a ribbon of equilateral triangles, with alternating folds in the same direction of 2arctan(√2/4) ≈ 38.931629° and 2arctan(√2) ≈ 109.471221°.

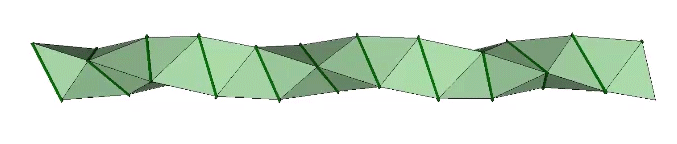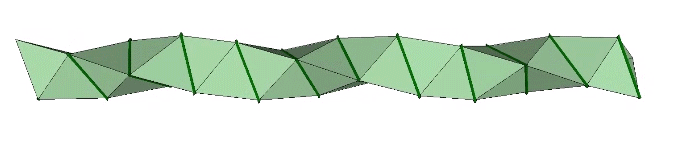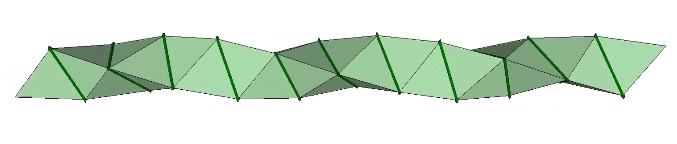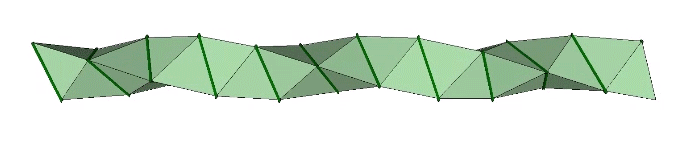
30-unit tetrahelix folded as a single helix (light green) which completes about 10 cycles.
Tetrahelix constructed as a counter-clockwise single helix folded from a single-wide ribbon of equilateral triangles. It completes about 10 cycles per 30 tetrahedra.

The double helix is folded from 2-panel-wide ribbon. The two panels are folded inward at 2arctan(√2/4) ≈ 38.931629°, and the individual triangles are folded in an alternating pattern of 2arctan(√2/5) ≈ 31.586338° away, and 2arctan(√2) ≈ 109.471221° away.

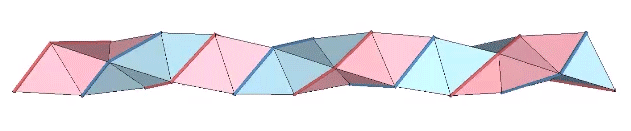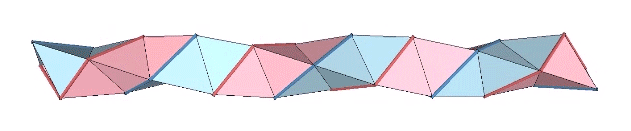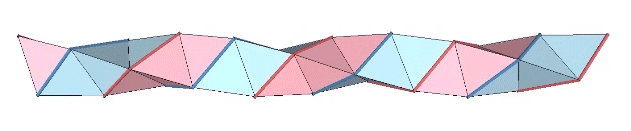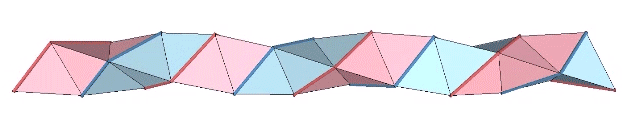
30-unit tetrahelix folded as double helix (pink and light blue) each of which complete about 5 cycles.
Tetrahelix constructed as a clockwise double helix from a double-wide ribbon of equilateral triangles. It completes about 5 cycles per 30 tetrahedra.

The triple helix is folded from 3-panel-wide ribbon. Each panel is folded the length of the ribbon at 2arctan(√2) ≈ 109.471221°. The individual triangles are folded in an alternating pattern of 2arctan(√2/4) ≈ 38.931629° away, and 2arctan(√2/5) ≈ 31.586338° toward.

30-unit tetrahelix folded as a triple helix (pink, light blue, and light green) each of which complete about 1 cycle.
Tetrahelix constructed as a counter-clockwise triple helix from a triple-wide ribbon of equilateral triangles. It completes about 1 cycle every 30 tetrahedra

A casual assessment of the triple helix might lead to the assumption that the two angles between which the three helices oscillate, i.e are folded in a repeating pattern of one fold up, and one fold down, etc., are the same angle. They are not. As a consequence, one tetrahelix cannot be nested with another. There is always a gap of approximately 7.356103°, which causes them to spring apart. Fuller called this gap the “unzipping angle”, and thought it might explain the behavior of replicating DNA molecules.

Three and two regular tetrahedron face-bonded about a single edge result in the concave and a convex angles of the triple-helices. Their difference is calculated and illustrated by an inset of the two combined into a 5-tetrahedron ring, clearly showing the gap.
The two dihedral angles of the triple-helices of the tetrahelix might at first glance appear identical. Fuller called the difference between the two the “unzipping angle,” in reference to the DNA molecule’s replication behavior.

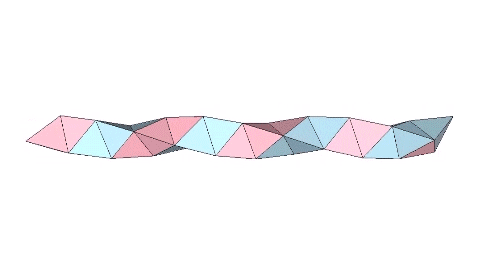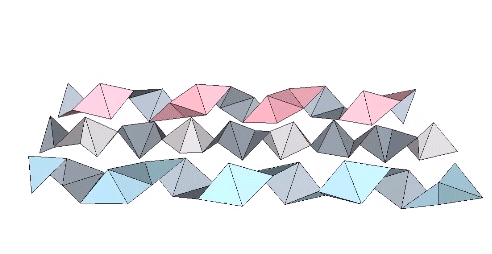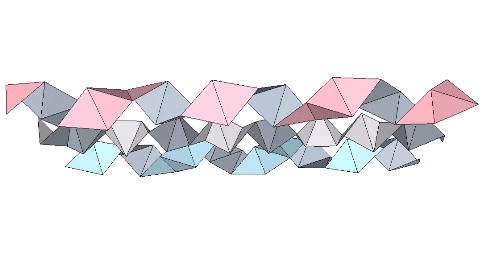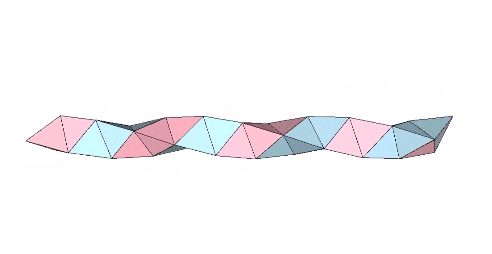
The models of the tetrahelix so far discussed are constructions that result in only the outer shell of the tetrahelix, i.e., a hollow tube with no interior faces. The interior faces can be folded from a separate strip. In the illustration below, two strips of triangles are folded and combined as a double helix that constitutes the surface of the tetrahelix, and a third strip of triangles is folded to constitute its internal structure. The third strip which is enclosed by the other two is is folded at angles of arctan(2√2) ≈ 70.528779° alternately toward and away. Its striking similarity to the structure of the DNA molecule, i.e. a double helix with paired connections, was not lost on Fuller.

Two ribbons (pink and light blue) each constituting one helix of a double-helix surrounding a third (gray) folded as the interior faces of a tetrahelix.
Two ribbons combine to form the surface a double helix, while a third provides the interior connections between them.

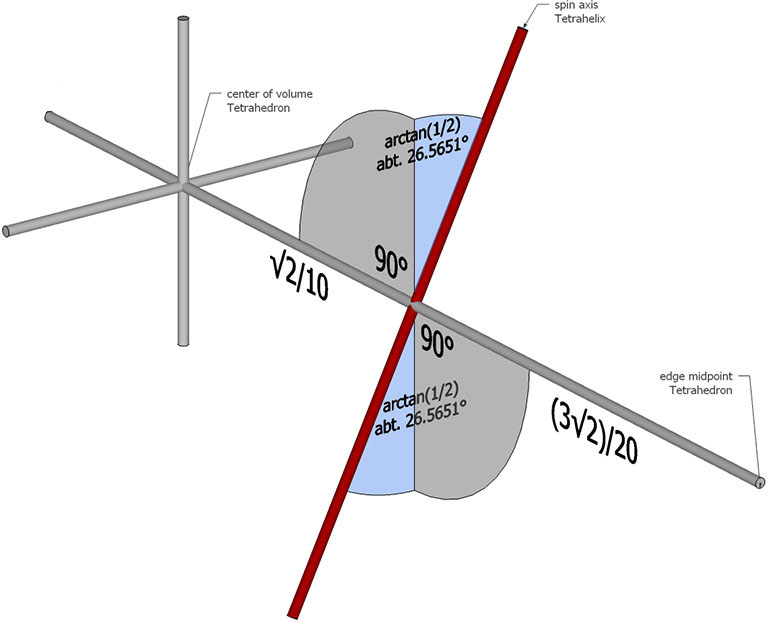
The helical axis does not pass through through the center of volume of any of its constituent tetrahedra. With the edge length taken as unity, the spin axis of the tetrahelix crosses an edge-to-edge axis of each tetrahedron perpendicularly at a distance of √2/10 from its center of volume, and is tilted at an angle of arctan(1/2), about 26.565051°.

The spin axis of the tetrahelix in relation to its constituent tetrahedrons' edge-to-edge axes and center of volume.
The spin axis of the tetrahelix (red) in relation to the tetrahedron’s edge-to-edge axes (gray) and center of volume.

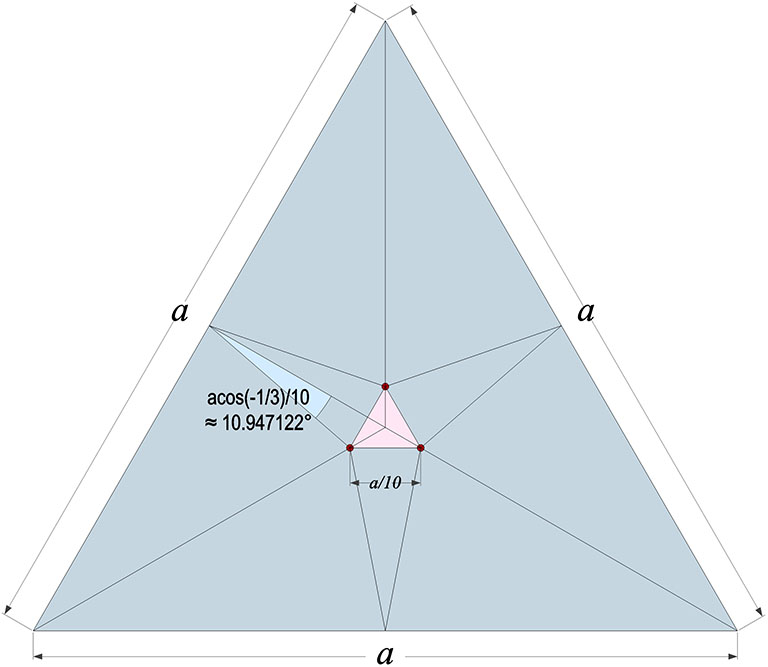
The point at which all possible spin axes pass through the tetrahedron’s faces appears to be precisely arctan(√2)/5, or about 10.947122° off-center along lines drawn from a vertex to the midpoint of the opposite edge. Their points of intersection form an equilateral triangle centered on the face with edge length 1/10th that of the face.

Face of tetrahedron showing the three possible points of intersection with tetrahelix axis.
The spin axis of the tetrahelix intersects the faces of its constituent tetrahedra at one of three points (red dots) defined by the vertices of an equilateral triangle (pink), centered on the face, with edge lengths 1/10th that of the tetrahedra.

Each tetrahedron is rotated about the helical axis at an angle of arctan(2/√5)+90°, or arccos(-2/3), about 131.810315°, from the one below it. Every third tetrahedron constitutes a “vertebra” of one of the three “spines” of the tetrahelix.

Triple helix viewed from the side, showing how the vertebrae of each spine mesh like the teeth of gears.
Triple helix viewed obliquely with the individual spines and vertebrae clearly defined.
Every third tetrahedron (pink, blue, and green) constitutes a vertebra of one of three spines (pink, blue and green) that run along the outer edges of the tetrahelix.

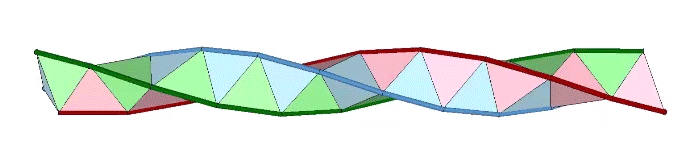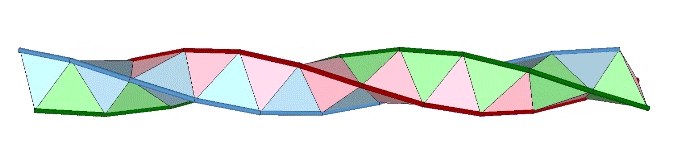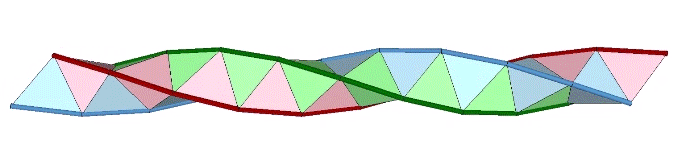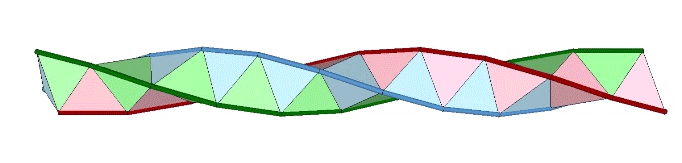
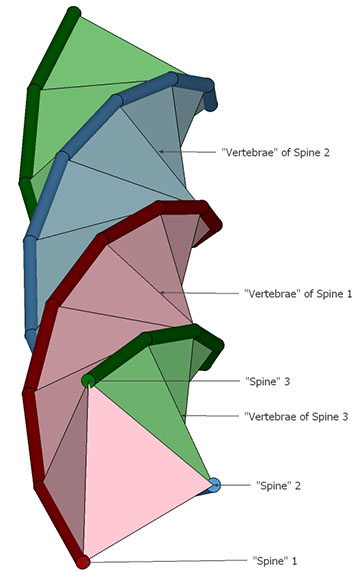
Curiously, the number of tetrahedra is not rationally commensurable with the helical cycle. The helix appears to complete one cycle every 30 tetrahedra, but careful measurement shows the rotation to be just short of 360°. Each vertebra is rotated at an angle of 3arctan(2/√5) – 90°, about 35.430945° from the previous. Ten vertebrae almost, but not quite, complete one 360° cycle. With r being the rotation per vertebra, the difference is 360-(10r) ≈ 5.690553°.

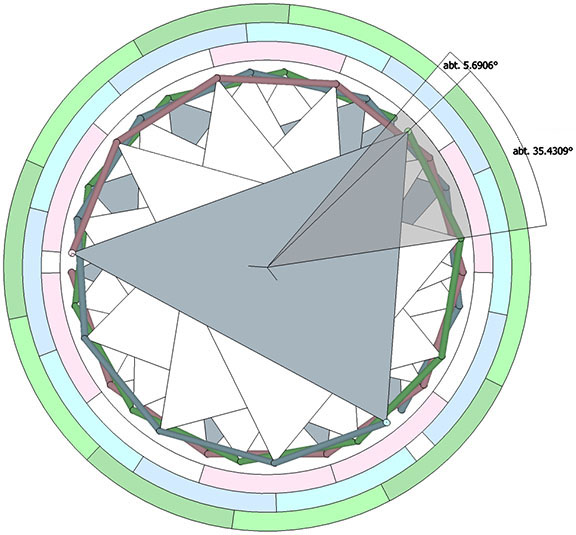
Tetrahelix viewed from the top and surrounded be three rings representing the spines of the triple helix. Each ring is divided by arcs representing the rotations of the vertebrae.
Tetrahelix viewed from the top. Three outside rings (pink, blue, and green) divided into arcs of ≈ 35.430945° indicate the degree to which each vertebra is rotated from the one below it in each of three spines of the same color. Ten rotations sum to a combined total of about 5.6906° less than 360°.

One might assume that one and only one helix may be formed from each of the four faces of the tetrahedron, i.e., that there are four (4) possible helical constructions. Further consideration may allow for clockwise and counter-clockwise helices, making for a total of eight (8) possibilities. Actually, there are twelve (12) unique axes upon which the helix can be constructed.

Each of the twelve axes can be illustrated with a cube placed inside a regular tetrahedron and sized such that four of its eight corners intersect the four faces of the tetrahedron as an equilateral triangle of edge length 1/10th that of the tetrahedron. Each of the twelve axes is described by lines connecting the vertices of the triangle with the center of the cube’s face with which it intersects.

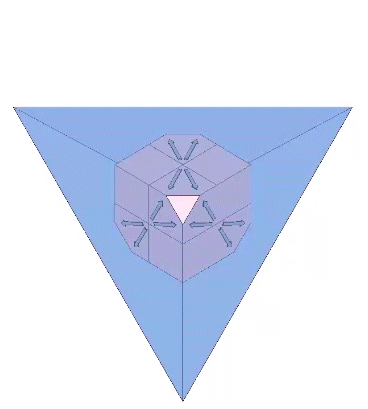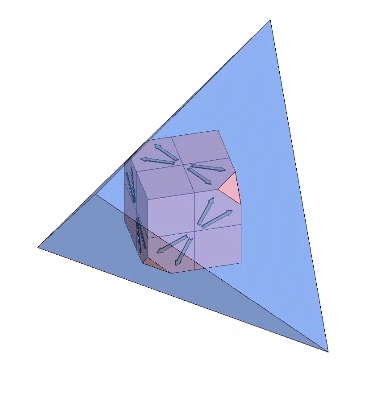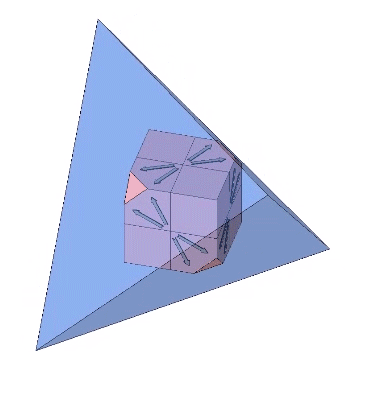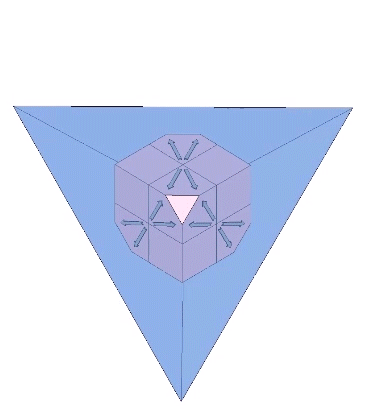
Cube inside a tetrahedron whose four faces have truncated four corners of the cube to form equilateral triangles of edge length one tenth that of the tetrahedron. Lines connect their vertices with centers of the cube's square faces.
The twelve potential axes of the tetrahelix can be illustrated with cube inside the tetrahedron with four corners intersecting the faces as a triangle with 1/10th edge-length of the tetrahedron.

The twelve unique helices alternate between clockwise and counter-clockwise constructions.

Twelve tetrahelices, six clockwise (blue) and six counterclockwise (pink) emerging from the faces of a common tetrahedron.
Twelve tetrahelices, six clockwise and six counter-clockwise, emerging from a single tetrahedron.

Given the fact that the number of tetrahedra is incommensurate with helical cycle, and the fact that its angles are all individually and mutually irrational, the number of configurations possible from serial inside-outing of tetrahedra, including the number of possible orientations of the individual tetrahedra in a fixed coordinate system, may be infinite.

Leave a comment