“… the tetra and VE are a priori incommensurable with the icosa. Despite this, the rhombic triacontahedron of tetravolume 5 (as a product of the icosa’s 15-greatcircle cleavaging), while under the oscillatory pressuring, is volumetrically and rationally coordinate with the tetrahedron and the state we speak of as matter, and when it is under the negative tensive pressure of the oscillatory Universe, it transforms from matter to radiation.”
—R. Buckminster Fuller, Synergetics, 987.058
The T quanta module was part of Fuller’s ongoing effort to find that elusive polyhedron of unit edge length whose tetrahedral volume was evenly divisible by 5. The 30-sided rhombic triacontahedron proved promising. It could be evenly subdivided into 120 irregular tetrahedron, each of which would have a volume of 5/120, or 1/24, i.e., the exact volume of his A and B quanta modules. Its edge lengths would be irrational, but when its in-sphere radius was taken as unit length, its calculated volume was almost, but not quite precisely, 5. The difference was so minuscule that Fuller initially dismissed it as due to the resolution of the trigonometry tables he was using.
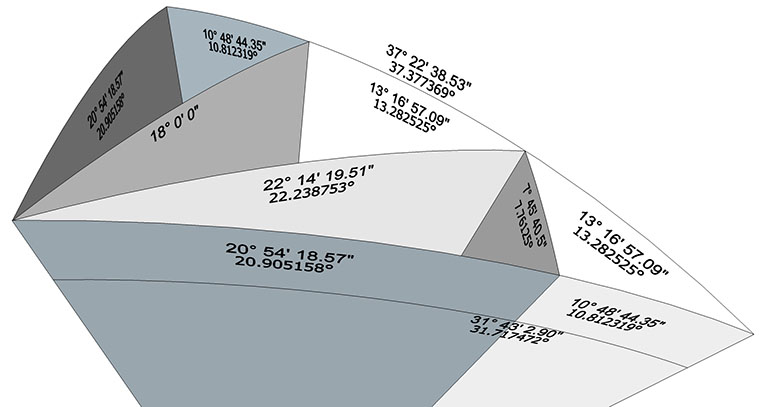
The T quanta module is associated with the basic disequilibrium LCD triangle which subdivides the surface of the sphere into 120 identical (60 positive and 60 negative) triangles. The 30 rhomboid faces of the triacontahedron may each be subdivided into four triangles for a total of 120 whose spherical form is the basic disequilibrium LCD triangle. (Note: The quartering of twelve rhomboid faces of the rhombic dodecahedron correspond to the basic equilibrium LCD triangle which divides the sphere into 48 identical (24 positive and 24 negative) triangles.)
To construct the T quanta module, a 5-tetra-volume rhombic triacontahedron is subdivided into 30 half-octahedra whose bases are its 30 rhomboid faces and whose apexes converge at its center of volume. Then, these 30 half-octahedra are subdivided into four irregular tetrahedra each, forming 120 T quanta modules, sixty positive and sixty negative.
The T quanta module has precisely the same volume as the A and B quanta modules, i.e. 1/24 the volume of the regular tetrahedron of unit edge length. We know this operationally (see Operational Geometry), because a) the triacontahedron was constructed to have a tetra volume of precisely 5, and b) 5 divided by 120 = 1/24.

The edge lengths of the T quanta module are based on the in-sphere radius of the 5-tetra-volume rhombic triacontahedron, shown by the letter r in the illustration below. Fuller initially took the in-sphere radius, r, to be of unit length, i.e., half the vector length in the isotropic vector matrix or the radius of the sphere. But he was later persuaded to amend this figure. The in-sphere diameter, 2r, of the rhombic triacontahedron with a tetra volume of 5 is approximately 0.999483. The quanta module with 2r equal to 1 was renamed the E quanta module, and a rhombic triacontahedron built of E quanta modules would have a tetra volume slightly greater than 5, approximately 5.007758.
Unfolded, the T and E modules would form a perfect square of edge length r if the face triangle (upper right in the illustration below) were flipped to expose its obverse side. This demonstrates, operationally, that the surface area (in squares) of the T and E quanta modules is precisely r². In equilateral triangles, the surface area would be 4r²/√3, but Fuller nonetheless took the square to be identical with r² and, by extension, mc², the physical manifestation of the generalized isotropic vector matrix’s prime vector raised to the second power, i.e., mass to energy. In other words, Fuller would model e=mc² as one T module quanta equal to the prime unit vector raised to the second power.
The in-sphere diameter of the tetra-volume 5 rhombic triacontahedron is approximately 0.000517 less than the prime unit vector. This is an exquisitely small difference, smaller than the thickness of a sheet of paper one might use to construct a T quanta module. The mass of the electron is approximately 0.000543 the mass of the proton. Fuller was led to conclude from this and a long list of other observations recounted in Section 986 of Synergetics 2, that the difference between the T quanta module of quanta volume 1, and the E quanta module with quanta volume of approximately 1.001551606, was the difference between energy as mass and energy as radiation.
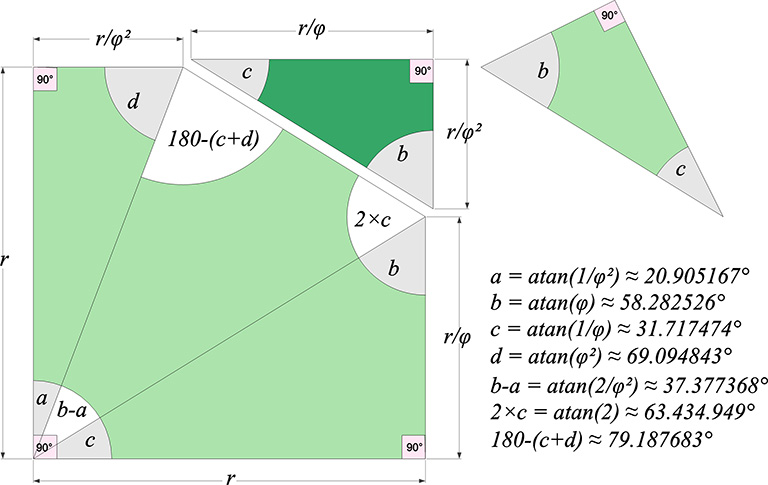
The dimensions of the T and E quanta modules are all related to the golden ratio (φ), (√5+1)/2. The lengths of the diagonals of the rhomboid face of the triacontahedron are related to the in-sphere diameter (d) and φ:
short diagonal = d/φ²
long diagonal = d/φ
The central and surface angles of the T and E quanta modules referenced in the above illustration are:
a = atan(1/φ²) ≈ 20.905167°
b = atan(φ) ≈ 58.282526°
c = atan(1/φ) ≈ 31.717474°
d = atan(φ²) ≈ 69.094843°
b-a = atan(2/φ²) ≈ 37.377368°
2×c = atan(2) ≈ 63.434.949°
180°-(c+d) = atan(2φ²) ≈ 79.187683°
Note that these angles are all identical to, or composed of, the surface and central angles of the Basic Disequilibrium LCD Triangle, the lowest common denominator of a spherical surface. This is consistent with Fuller’s proposition that the rhombic triacontahedron of tetra volume 5 “has the maximum limit case of identical tetrahedral subdivisibility, i.e., 120 subtetra.” (Synergetics, 986.412)