“The rhombic dodecahedron’s 144 modules may be reoriented within it to be either radiantly disposed from the contained sphere’s center of volume or circumferentially arrayed to serve as the interconnective pattern of six 1/6th spheres, with six of the dodecahedron’s 14 vertexes congruent with the centers of the six individual 1/6th spheres that it interconnects. The six 1/6th spheres are completed when 12 additional rhombic dodecahedra are close-packed around it. The fact that the rhombic dodecahedron can have its 144 modules oriented as either introvert-extrovert or as three-way circumferential provides its valvability between broadcasting-transceiving and noninterference relaying. The first radio tuning crystal must have been a rhombic dodecahedron.”
— R. Buckminster Fuller, Synergetics, 426.41-42
The isotropic vector matrix modeled as A and B quanta modules discloses two rhombic dodecahedra, one occupying the positions of the spheres, and the other the space between the spheres. The two constructions can be shown to exchange places during the jitterbug transformation, which to me is strong validation of the models. See also: Spheres and Spaces.
The close-packing of spheres around a central nucleus form successive shells of cuboctahedra, and defines the polyhedron that Fuller called the vector equilibrium (VE ). We can construct the VE in A and B quanta modules by joining around a common center the quanta module constructions of eight regular tetrahedra and six half-octahedra.
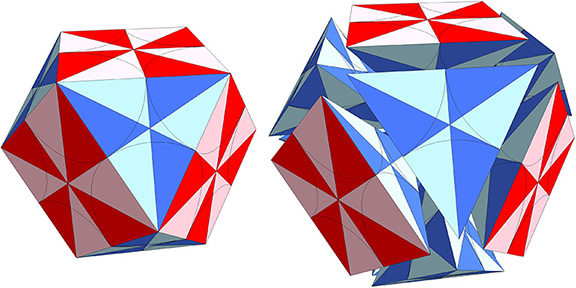
At the center of this construction we have inadvertently constructed a rhombic dodecahedron, which elegantly corresponds to the nuclear sphere of the close-packed array.
In the quanta module construction of the isotropic vector matrix, it can be shown operationally that the same rhombic dodecahedron occurs at each of the vector equilibrium’s twelve exterior vertices, coinciding with the twelve spheres in the first shell of spheres radially close-packed around a central nucleus.
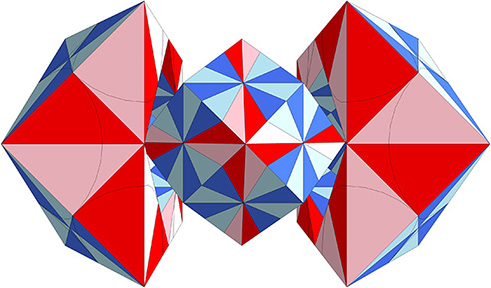
Curiously, another rhombic dodecahedron occurs between vector equilibria in the matrix, that is, in the spaces between the spheres.
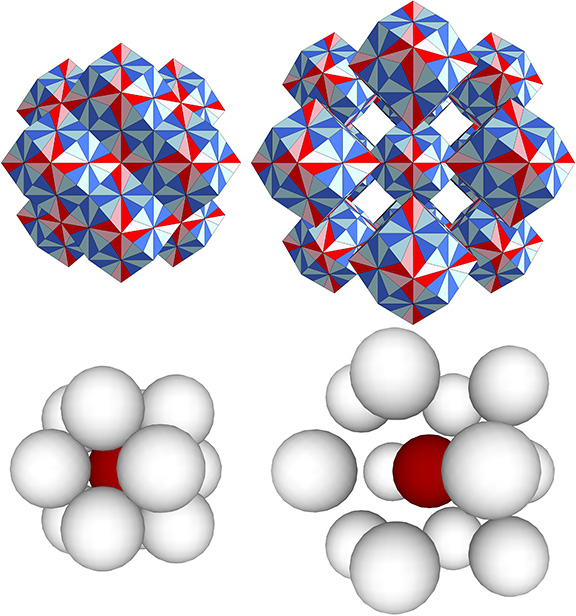
In the interstitial model of the isotropic vector matrix, the space between spheres is disclosed to be a concave vector equilibrium at the centers of the octahedra.
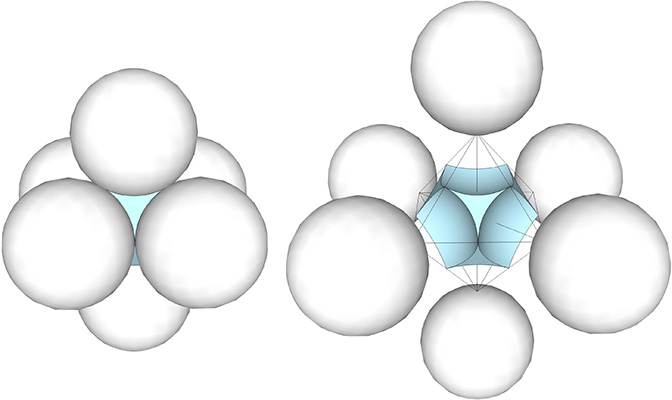
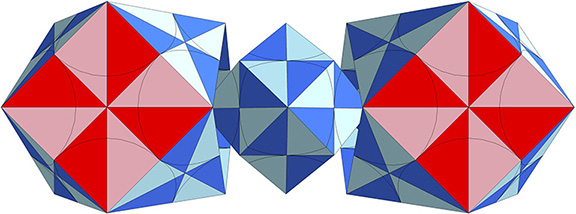
Because spaces in the isotropic vector matrix are occupied by concave vector equilibria, Fuller conceived of spheres as convex vector equilibria (see Spheres and Spaces). During the jitterbug transformation, these two rhombic dodecahedra exchange places, i.e., the spaces become spheres and the spheres become spaces. Fuller imagined the spaces to be spheres turned inside-out; the concave VE discloses the sphere’s interior (concave) surface. This conception of the jitterbug transformation is reinforced in the two quanta module constructions of the rhombic dodecahedron, as the following illustration should make clear.

We can turn one quanta module construction of the rhombic dodecahedron into the other by dividing it into six irregular octahedra and then flipping them 180° so that the center becomes the surface (or vice versa). See also: Anatomy of a Sphere; and Spheres and Spaces.