“The whole of synergetics’ cosmic hierarchy of always symmetrically concentric, multistaged but continually smooth (click-stop subdividing), geometrical contracting from 20 to 1 tetravolumes (or quanta) and their successive whole-number volumes and their topological and vectorial accounting’s intertransformative convergence-or-divergence phases … elucidate conceptually, and by experimentally demonstrable evidence, the elegantly exact, energetic quanta transformings by which:
- energy-exporting structural systems precisely accomplish their entropic, seemingly annihilative quantum “losses” or “tune-outs,” and;
- new structural systems appear, or tune in at remote elsewheres and elsewhens, thereafter to agglomerate syntropically with other seemingly “new” quanta to form geometrically into complex systems of varying magnitudes, and how;
- such complex structural systems may accommodate concurrently both entropic exporting and syntropic importing, and do so always in terms of whole, uniquely frequenced, growing or diminishing, four-dimensional, structural-system quantum units.”
—R. Buckminster Fuller, Synergetics, 270.11
With the regular tetrahedron as the unit measure of volume, most of the regular polyhedra have whole number or rational volumes. Fuller takes credit for this discovery and considered it one his most significant.
| Image | Polyhedron | Volume in Tetrahedra | Quanta Modules |
|---|---|---|---|
 | Tetrahedron | 1 | Total: 24; A: 24; B: 0 |
 | Half Octahedron | 2 | Total: 48; A: 24; B: 24 |
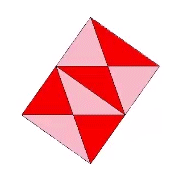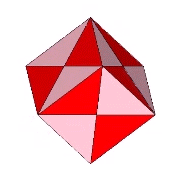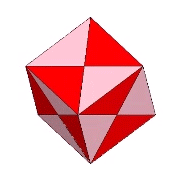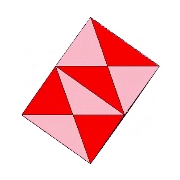 | Cube (unit diagonal) | 3 | Total: 72; A: 48; B: 24 |
 | Octahedron | 4 | Total: 96: A: 48; B: 48 |
| Rhombic Triacontahedron | 5 | Total: 120: A: 0; B: 0; T: 120 | |
 | Rhombic Dodecahedron | 6 | Total: 144; A: 96; B: 48 |
Note that the volume 5 rhombic triacontahedron is constructed, uniquely, of T quanta modules. Though the T module is identical in volume to the A and B quanta modules, and therefore rationally commensurate with the regular tetrahedron, all of its edge lengths—and the edge lengths of the rhombic triacontahedron constructed from them—are irrational. The in-sphere diameter of the volume 5 rhombic triacontahedron—and the outside edge of the unfolded T Module (×2)—is about 0.9994833324, so very close to 1 that Fuller assumed it had to be a computational error. Mathematicians eventually convinced him that the difference was real and measurable. For further discussion on this topic, see T and E Quanta Modules.
Other polyhedra so far discovered with whole number volumes in tetrahedra include the Kelvin truncated octahedron with a volume of 96, the pyritohedron, with a volume of 24, and, presumably, the tetrakaidecahedron of the Weaire-Phelan matrix which should have the same volume as its companion pyritohedron. See The Kelvin Truncated Octahedron, and; Pyritohedron Dimensions and Whole-Number Volume.