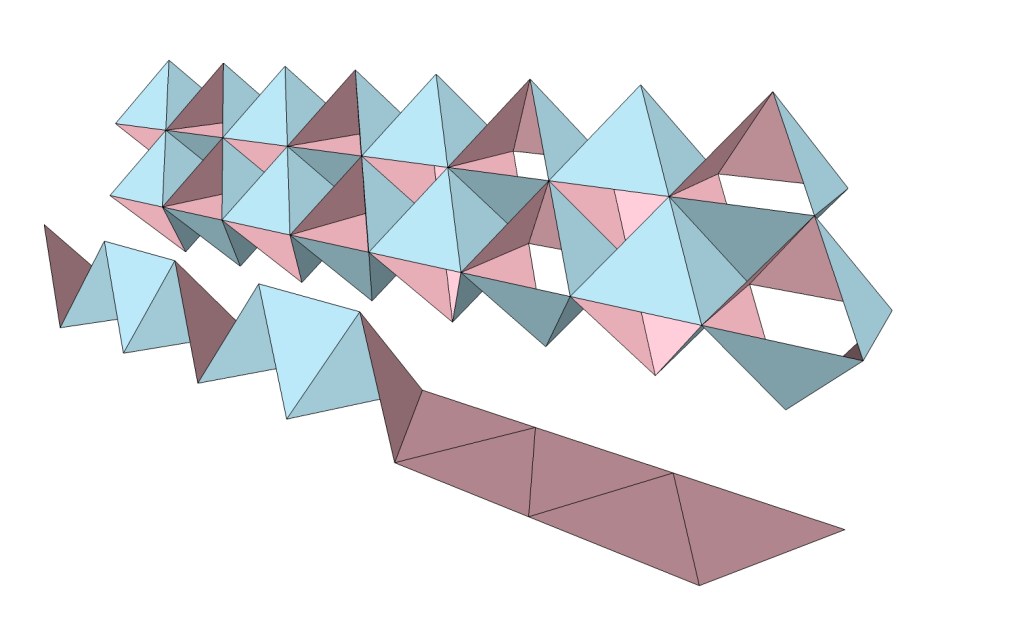
The tetrahedron, rhombic dodecahedron, octahedron, and icosahedron can all be constructed from the sequential linear folds of a single paper strip. Fuller was interested in the shapes of polyhedron nets, especially those of the quanta modules, but does not seem to have devoted much time (nor has anyone else for that matter) to nets that fold into their respective polyhedra sequentially from a single linear strip. I’m drawn to these constructions because their wave-like patterns suggest, at least to my mind, the transformation of potential energy into radiant energy.
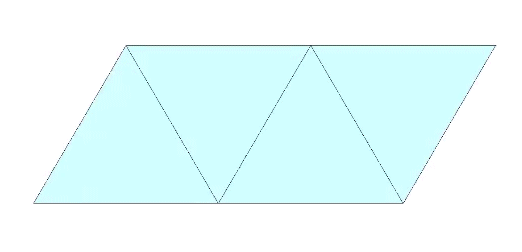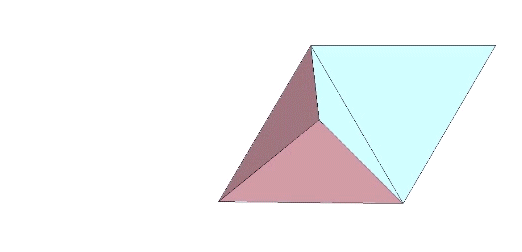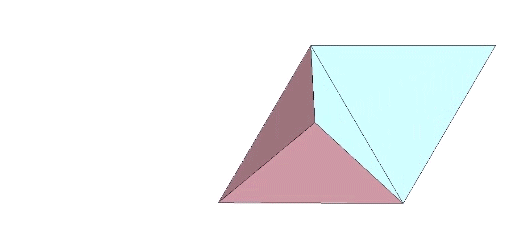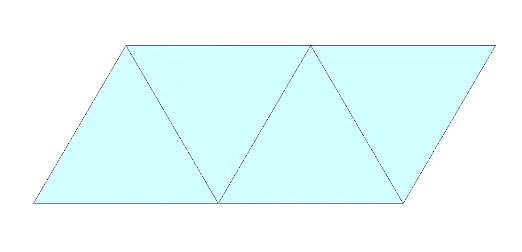
Three sequential folds of 2arctan(√2) each, or approximately 109.4712°, produce the regular tetrahedron.

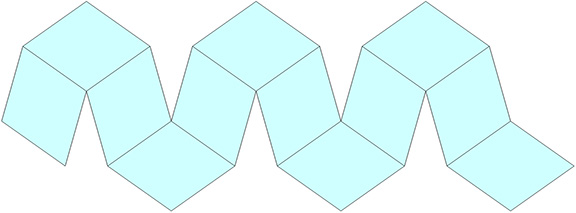
Eleven sequential folds of 60° each produce the the rhombic dodecahedron.

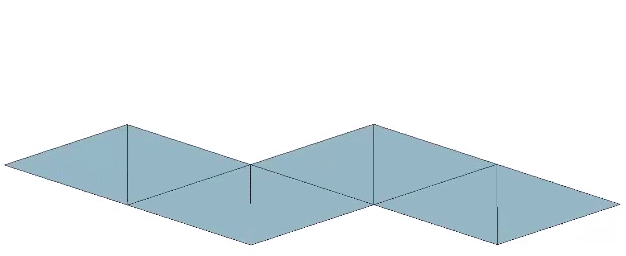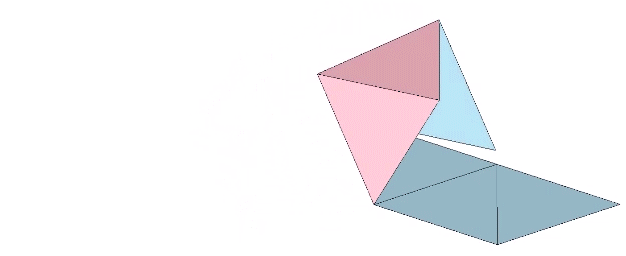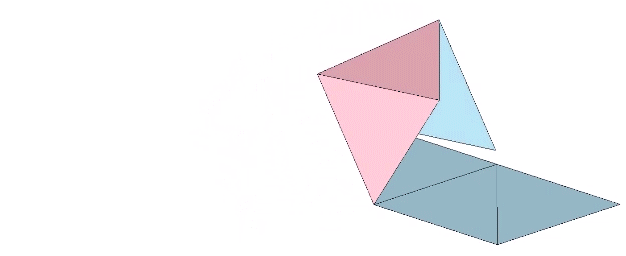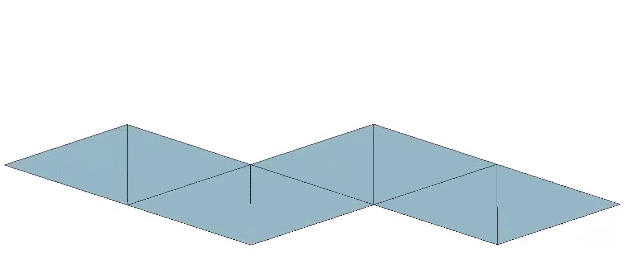
Seven sequential folds of arctan(√2) each, or approximately 70.5288°, produce the octahedron.

One positive and one negative tetrahedron can be unfolded to form an octahedron, suggesting the neutrality of the octahedron, as well as the gain and loss of quanta modeled in respective volumes, with the two tetrahedra having a combined volume of 2, and the octahedron having a volume of 4.
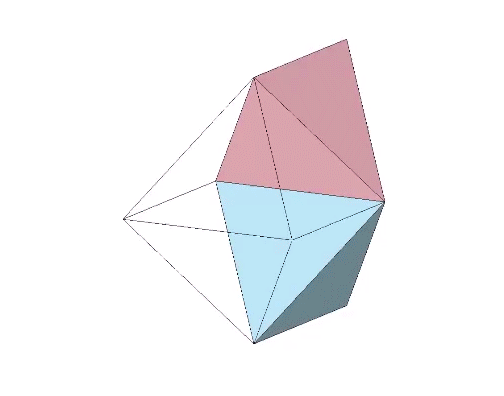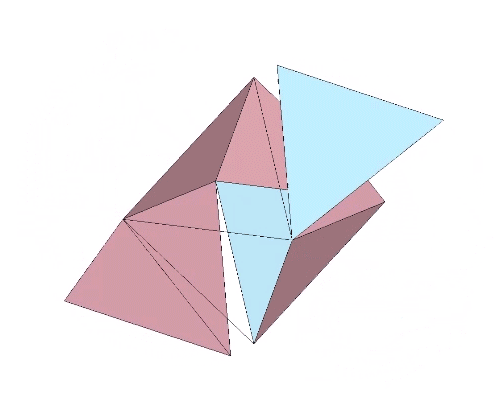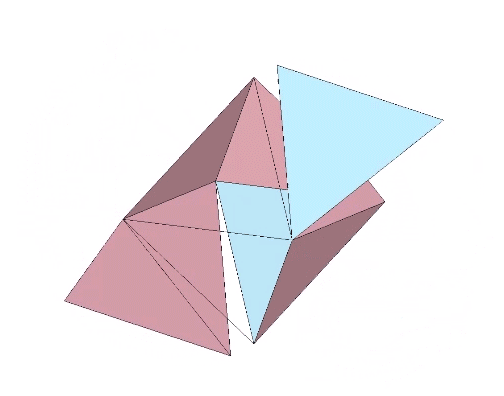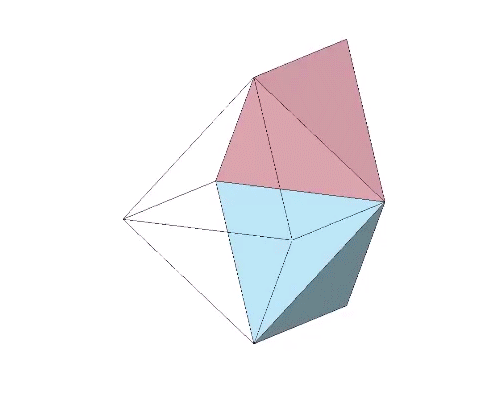
Nineteen sequential folds of arctan(2/√5) each, or approximately 41.8103°, produce the icosahedron.

If we alternate the folds, one positive and two negative, linear ribbons of equilateral triangles will form edge-bonded half octahedra which, repeated indefinitely, form a continuous chain of polarized octahedra and tetrahedra spaces. The chains may be combined, placed parallel or perpendicular to one another, to form the the isotropic vector matrix. See also: The Isotropic Vector Matrix as Transverse Waves.