Jitterbugging into and out of its ground state, the isotropic vector matrix seems to reach maximum disequilibrium (i.e. maximum expansion) when the contracting vector equilibria (VEs) and expanding octahedra both describe regular icosahedra. It can be shown, however, that the contracting VEs and expanding octahedra cannot pass through their icosahedral phases simultaneously. While one has expanded or contracted into a regular icosahedron, the other describes an irregular icosahedron that complements the other to maintain an unbroken array of face-bonded polyhedra.
Precisely midway through the jitterbug, both the collapsing VEs and the expanding octahedra describe an irregular icosahedron identical with the six-strut tensegrity sphere which, when combined to fill all-space, forms the tensegrity model of the isotropic vector matrix. See also: Tensegrity. The polyhedron associated with the six-strut tensegrity sphere is now more commonly known as the Jessen orthogonal icosahedron, but in Fuller’s geometry it is more accurately described as the spherical form of the tensegrity tetrahedron. This phase seems to be the true equilibrium phase of the jitterbug, or what I’m now calling the tensegrity, or tensor equilibrium phase—the vector equilibrium phases, i.e., the VE and octahedron phases, being the extremes. See: Tensegrity Equilibrium and Vector Equilibrium.
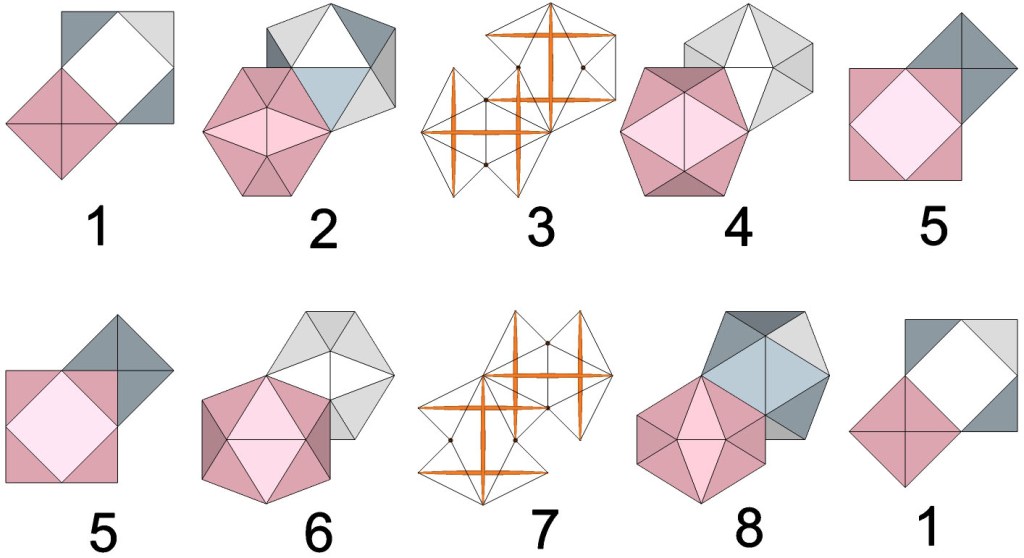
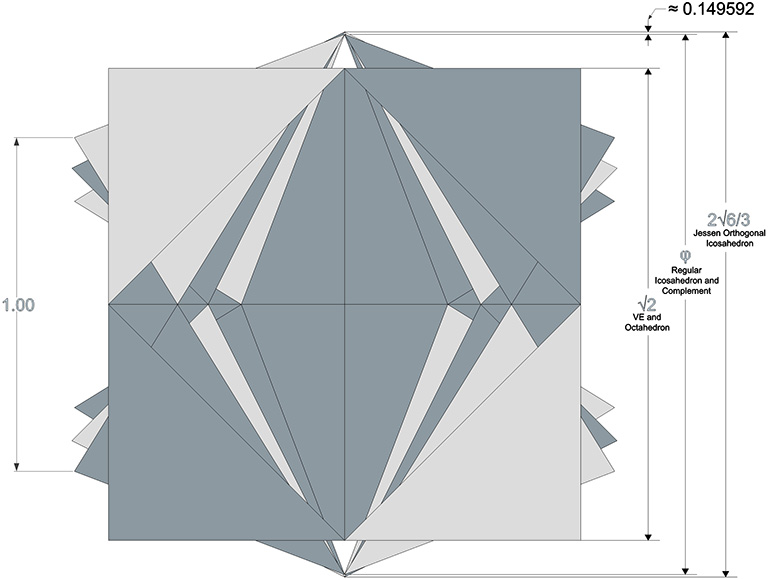
The six-strut tensegrity sphere describes an irregular icosahedron whose cubic domain is less than 1% larger than that of the the regular icosahedron and its complement. With unit edge lengths, the cubic domain of the jitterbugging VE increases from φ (the golden ratio, (√5+1)/2) at the phases of the regular icosahedron and its complement, to 2√6/3, a difference of only about 0.149592.
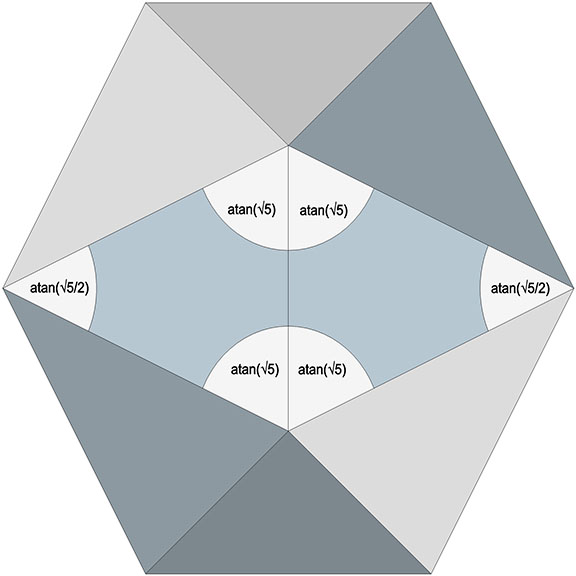
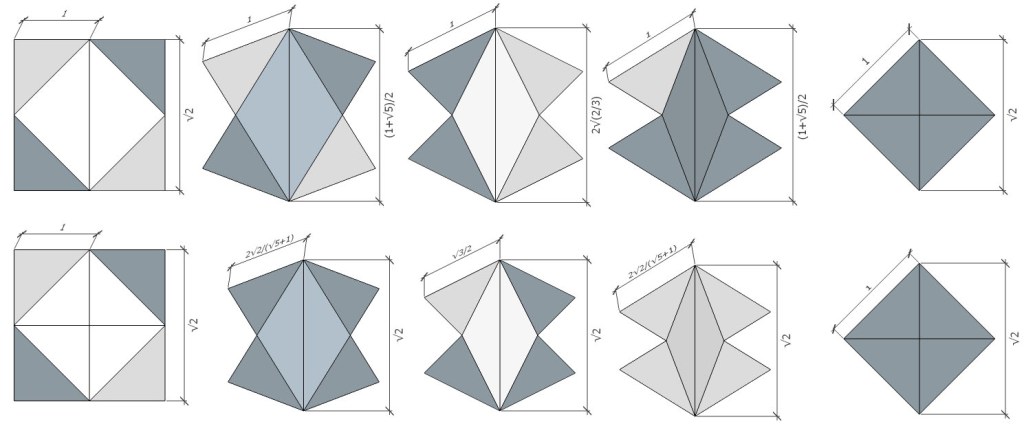
Represented as a convex polyhedron, eight of the twenty faces of the Jessen orthogonal icosahedron remain equilateral triangles (all angles 60°), while the remaining twelve, corresponding to the six open square faces of the VE, are isosceles triangles whose angles are atan(√5/2) and atan(√5), approximately 48.189685°, and 65.905157°.
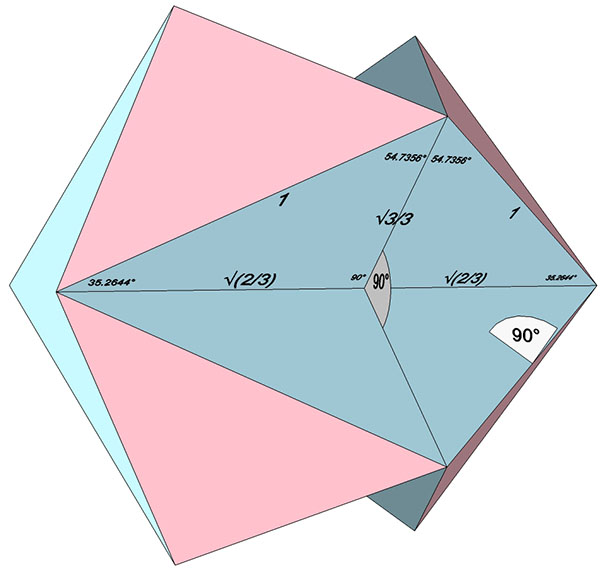
The polyhedron that most closely resembles the six-strut tensegrity sphere draws the vector along the long diagonal (rather than the short diagonal) of the skewed square. This construction forms the concave polyhedron identified as the Jessen Orthogonal Icosahedron, so named because its dihedral (face-to-face) angles are all 90°. Curiously, the angles of the its concave faces, atan(√2/2) and atan(√2) (approx. 35.2644° and 54.7356°) are also found in the tetrahedron and A quanta module, which suggest that that the Jessen may have a rational volume in tetrahedra.
In fact, if the long edge of the Jessen’s concave face is held at √2 (as shown below for the jitterbugging of the 6-strut tensegrity sphere) its tetrahedral volume is precisely 7.5. If the Jessen’s concavities are filled in, its volume is exactly 10.5 unit tetrahedra. The concavities alone have a volume of 3. The same tetrahedral volume as the unit-diagonal cube.
Curiously, the Jessen orthogonal icosahedron is a dual of the pyritohedron. The pyritohedron is associated with the close-packing of bubbles and foams in the Weaire-Phelan matrix, and is the polyhedral domain of unique nuclei in the isotropic vector matrix. See: Formation and Distribution of Nuclei in Radial Close-Packing of Spheres, and; Tetrakaidecahedron and Pyritohedron.
The jitterbug transformation may be modeled by alternately squeezing the struts of the six-strut tensegrity inward to form the octahedron, and pulling the struts outward to form the VE.
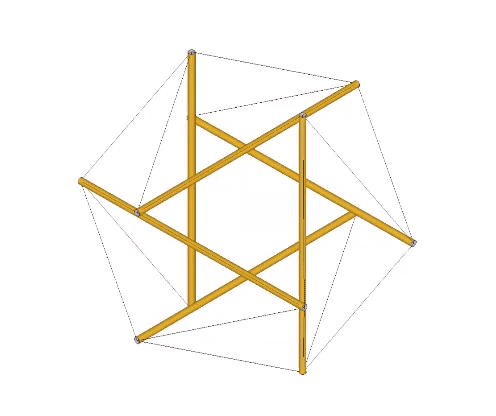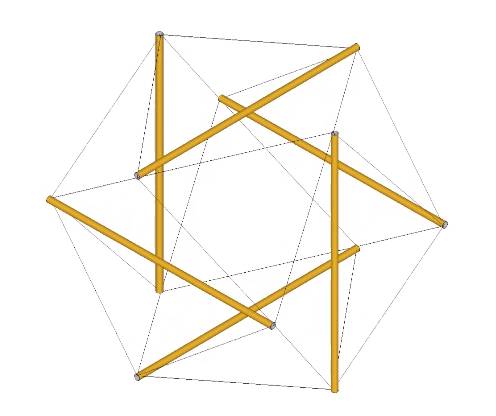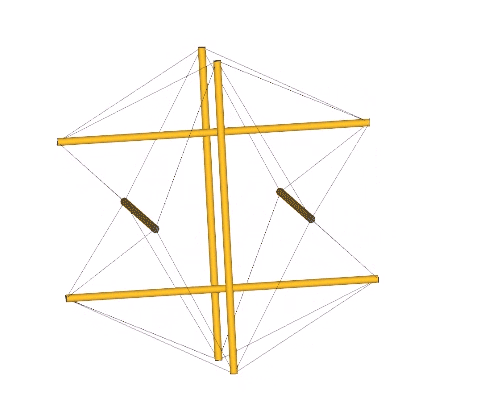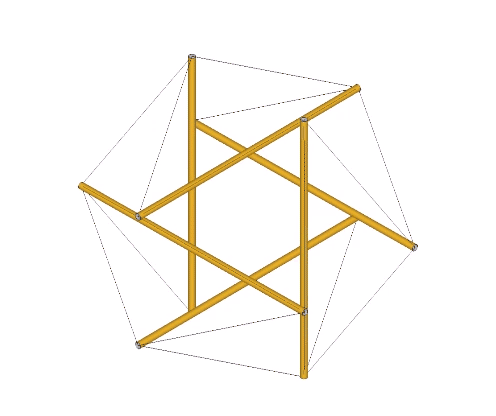
If we allow the tendons of the six-strut tensegrity sphere to stretch while the struts maintain their length of √2 at vector equilibrium, we find that the tendon length increases from √3/2 (approximately 0.866) at tensegrity equilibrium to 1.0 at vector equilibrium. Between tensegrity and vector equilibrium, the icosahedron and its complement have a tendon-edge length of 2√2/(√5+1), or √2/φ, approximately 0.874032.
The concave forms of the regular icosahedron and its complement have, despite their different shapes, identical face angles: eight equilateral triangles (60°, 60°, 60°) and twelve isosceles triangles of 36°, 36°, 54°.

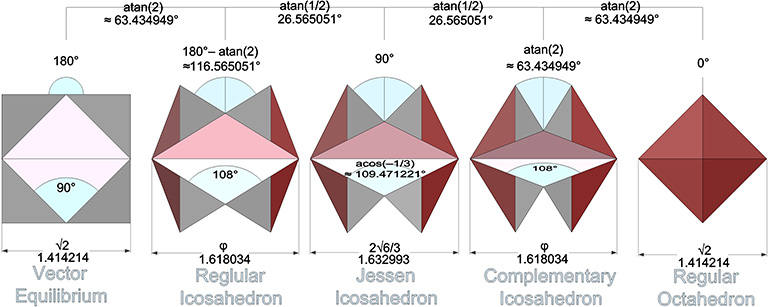
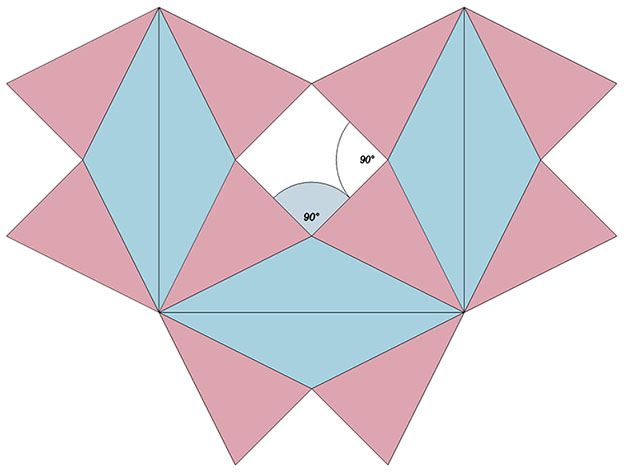
The dihedral angles of the concave polyhedra oscillate between 0° and 180°, passing through: arccos(-√5/5) ≈ 116.5605° at the regular icosahedron phase; 90° at the Jessen phase; and arctan(2) ≈ 63.4349° at the complementary icosahedron phase. The reduction or increase of the angles between phases follows the pattern: arctan(2); arctan(1/2); arctan(1/2); arctan(2); arctan(1/2), etc.
The face angles of the concave polyhedra oscillate between 0° and 180°, passing through: 36° and 108° at the regular icosahedron and its complement phases; and arctan(√2/2) ≈ 35.3644° and arccos(-1/3) ≈ 109.4712° at the Jessen phase.
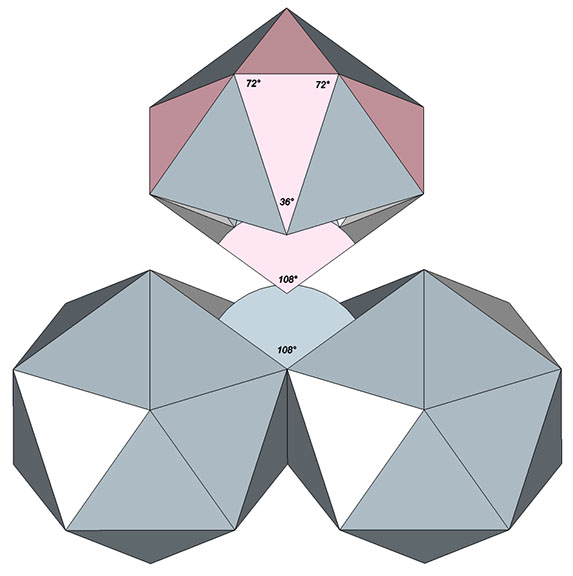
The space-filling complement to the regular icosahedron when represented as a convex polyhedron has rational, whole-number face angles of 36°, 72°, and 72°, the same angles that constitute the golden triangle. Its internal edge-to-edge angles of 108° (3/10 of 360°) match the inter-edge angles of close packed convex regular icosahedra so that one nests transversely between the others.
The concave faces of the regular icosahedron and its complement form symmetrical “holes” that tunnel perpendicularly through the matrix with angles of 2×atan(φ) and 2×atan(1/φ) or atan(2), approximately 116.56505° and 63.43495° respectively.
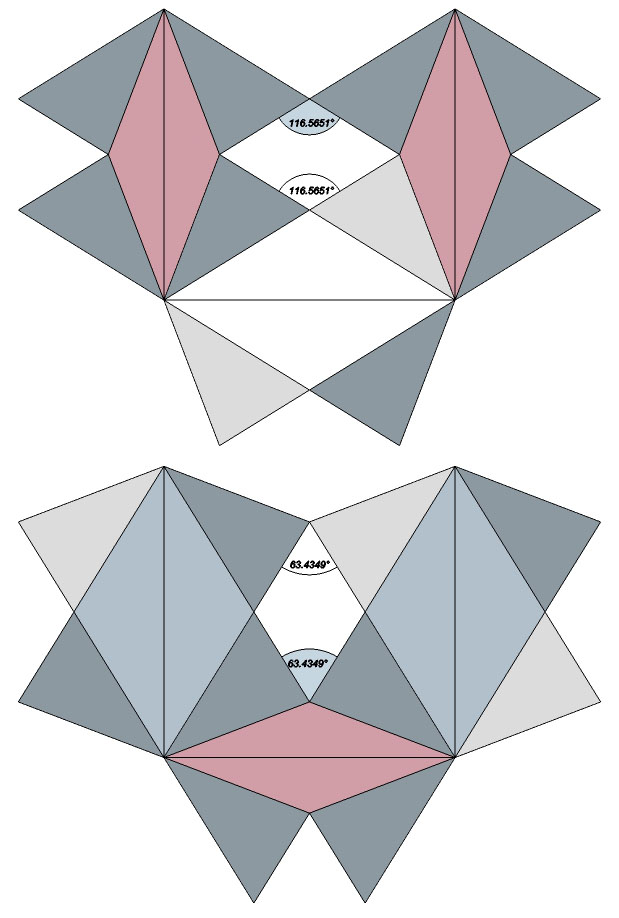
At tensegrity equilibrium the dihedral angles approach 90° and the transverse “holes” are orthogonal.
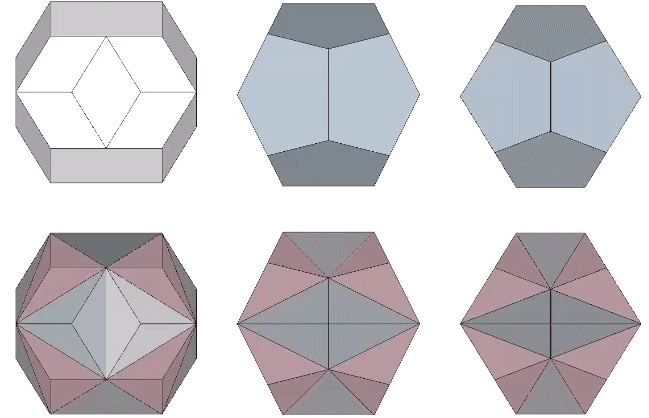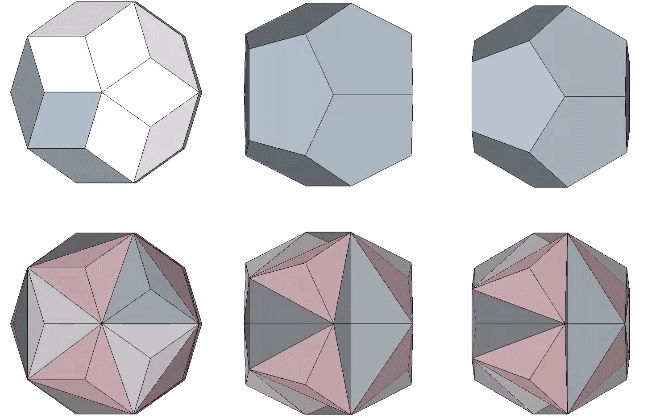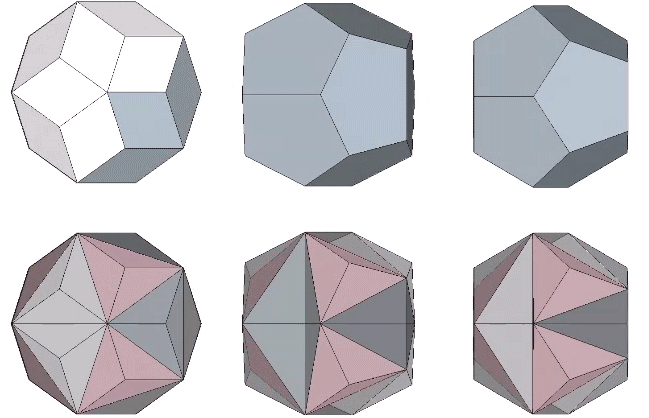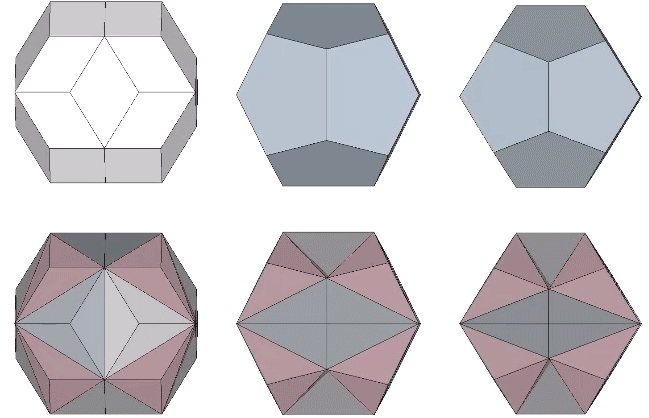
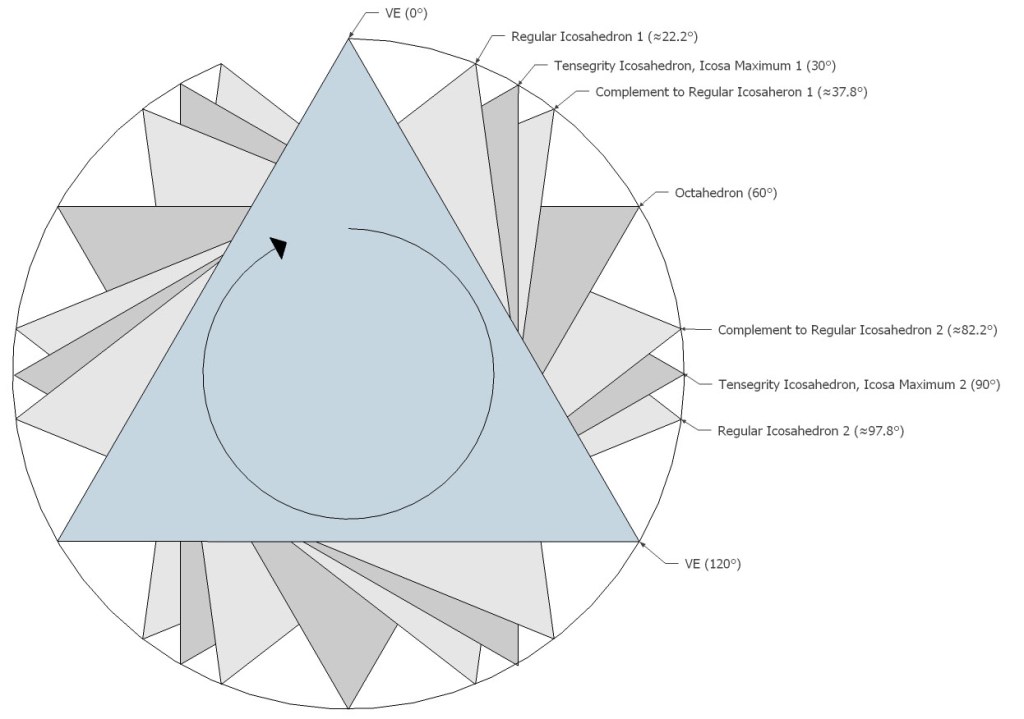
In the following illustration, the sequence of polyhedral transformations is shown in relation to the the angular rotation of the equilateral triangles in the vector model of the jitterbug.
From the vector equilibrium (VE) phase, a rotation of arctan(√(5/3))-30° (approximately 22.23875°) produces the regular icosahedron. Additional rotations of arctan(√(3/5))-30° (approximately 7.76125°) produce the Jessen icosahedron at 30°, and the space-filling complement to the regular icosahedron at arctan(√(3/5)) (approximately 37.76125°). Another rotation of 22.23875° produces the Octahedron at 60°. From the octahedron phase the rotation can reverse direction or continue to produce the complement to the regular icosahedron at arctan(√(5/3))+30° (approximately 82.23875°), the Jessen icosahedron at 90°, the regular icosahedron at arctan(√(3/5))+60° (approximately 97.76125°), and the VE again at 120°.
Significantly, these same angles appear in the Basic Disequilibrium LCD Triangle, and the Icosahedron Inside the Octahedron.
The three icosahedra—the regular, the Jessen, and the space-filling complement to the regular icosahedron—are truncations or duals of the rhombic triacontahedron, pyritohedron, and pentagonal dodecahedron, respectively.