Icosahedron Inside Octahedron

Greg Frederick

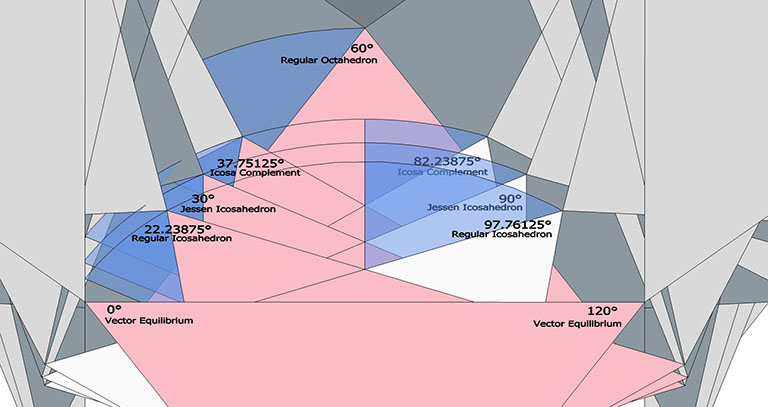
The regular icosahedron can be nested inside the regular octahedron so that eight of its faces are coincident with the eight faces of the enclosing octahedron.

The icosahedron inscribed inside a wireframe model of the octahedron.
The regular icosahedron inscribed within the regular octahedron

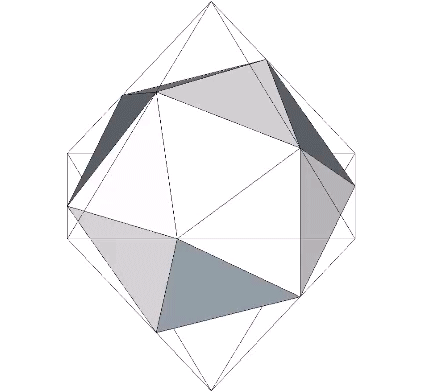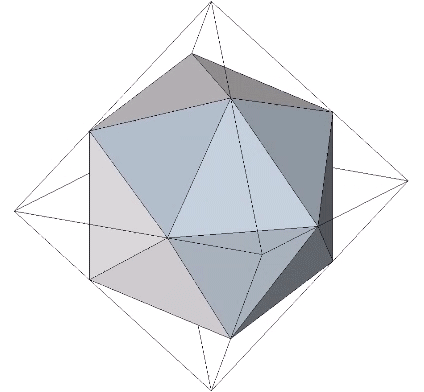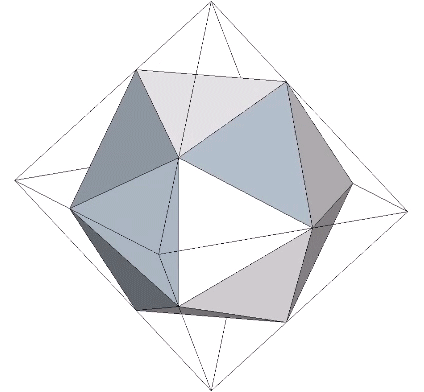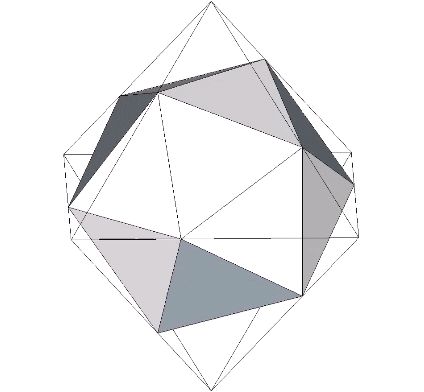
The icosahedron’s face is skewed at an angle of 37.76125° (arctan(√(3/5)) from the face of the octahedron and divides its edges into lengths corresponding to golden ratio (Φ).

Icosahedron inscribed in a wireframe model of the octahedron with angles and edge lengths indicated.
The face of the inscribed icosahedron divides the octahedron’s unit edge into 1/φ and 1/(1+φ), at angles of arctan(√(3/5)) ≈ 37.76125° and arctan(√(5/3)+30°) ≈ 82.23875°.

The same relationship is disclosed in the 31 great circles of the icosahedron. The faces of both the spherical octahedron and the spherical icosahedron are divisible by whole numbers of the Basic Disequilibrium LCD Triangle.

Sphere inscribed with the 31 great circles of the icosahedron with the 60 positive and 60 negative basic disequilibrium LCD triangles shown in white and light blue. The face of the spherical octahedron is shown in light gray and contains the face of the inscribed icosahedron shown in steel blue.
The 31 great circles of the icosahedron (and the 120 Basic Disequilibrium LCD Triangles) disclosing the spherical icosahedron inside the spherical octahedron in exactly the same orientation shown above.

The projection of the Basic Disequilibrium LCD Triangle onto the regular icosahedron discloses the same angles at which the icosahedron’s face is skewed from the face of its enclosing octahedron: 37.76125° (arctan(√(3/5)) and 82.23875° (arctan(√(5/3)+30°).

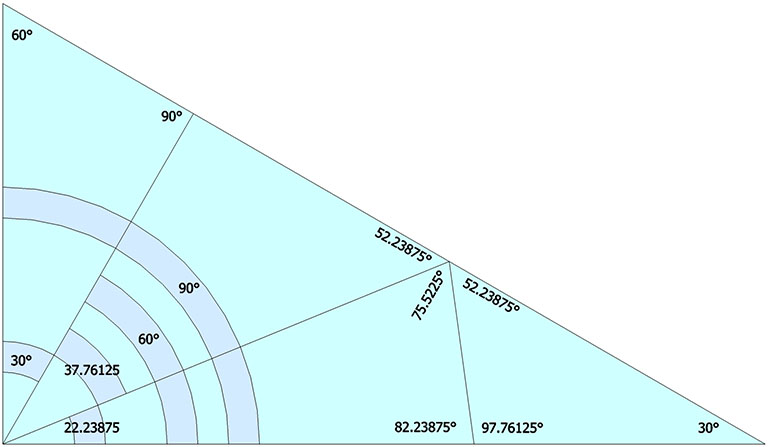
Planar projection of the spherical LCD triangle onto the face of the regular icosahedron.
Projection of the Basic Disequilibrium LCD Triangle onto the face of the regular icosahedron. The three angles comprising the right angle are identical with the rotations of the jitterbug

The angles at which the icosahedron’s face is skewed from the face of the enclosing octahedron are identical with the angles of rotation in the jitterbug corresponding to the space-filling complement to the regular icosahedron. See: Icosahedron Phases of the Jitterbug.

Note further that all of the surface angles in the icosahedron projection of the spherical LCD triangle are identical with the rotations in the jitterbug: the regular icosahedron at 22.23875° (arctan(√(5/3)-30°) and 97.76125° (arctan(√(3/5)+60°); the Jessen icosahedron or tensegrity equilibrium at 30° and 90°; the space-filling complement to the regular icosahedron at 37.76125° (arctan(√(3/5)) and 82.23875° (arctan(√(5/3)+30°), and the regular octahedron at 60°.

Rotations of the jitterbug presented as a single-frame time-sequence image of one triangle in its vector equilibrium, regular, Jessen, and complementary icosahedron, and octahedron phases, with angles of rotation indicated.
The rotations of the jitterbug corresponding to the regular icosahedron, the Jessen icosahedron, and the space-filling complement to the regular icosahedron, the octahedron, and the vector equilibrium.

Leave a comment