In Fuller’s energetic geometry, the great circles of the VE and icosahedron model energy transference and containment. He described them as “railroad tracks” which either move energy from one domain to another, or divert energy into into loops or holding patterns. (See: Great Circles: The 31 Great Circles of the Icosahedron, and; Great Circles: The 25 Great Circles of the Vector Equilibrium (VE).) What interested Fuller in his bow-tie models was their resolution of this idea with the apparent contradiction of two vectors passing through the same point simultaneously. As bow-ties, the great circle energy loops would simply deflect off one another at the vertices, keeping to their own holding patterns without the need to cross paths. All seven of the great circle sets of the VE and the Icosahedron are recapitulated in the bow-tie models described here and in Great Circle Bow-Ties of the VE. Both, I think, serve as quiet validation of Fuller’s intuitions.
The exterior angles of the Basic Disequilibrium LCD triangle is defined by the 15 great circles of the icosahedron, i.e., the geodesics described by its 15 edge-to-edge axes of spin. As with most (perhaps all) spherical polyhedra derived from great circles, its faces (the 120 LCD triangles) can be constructed from bow tie shapes folded from those great circles along fold lines laid out by their central angles. The central angles of the LCD triangle are: atan(1/φ) ≈ 31.717474°; atan(1/φ²) ≈ 20.905157°, and atan(φ) – atan(1/φ²) ≈ 37.377368°, where φ = the golden ratio, (√5+1)/2. These are laid out on each of the 15 great circle disks as shown in the illustration.

The 10 great circles of the icosahedron are the geodesics described by the regular icosahedron’s 10 face-to-face axes of spin. They describe the spherical vector equilibrium VE as well as a spherical polyhedron that aligns with the 2F Class 1 geodesic icosahedron. (See: Geodesics.)
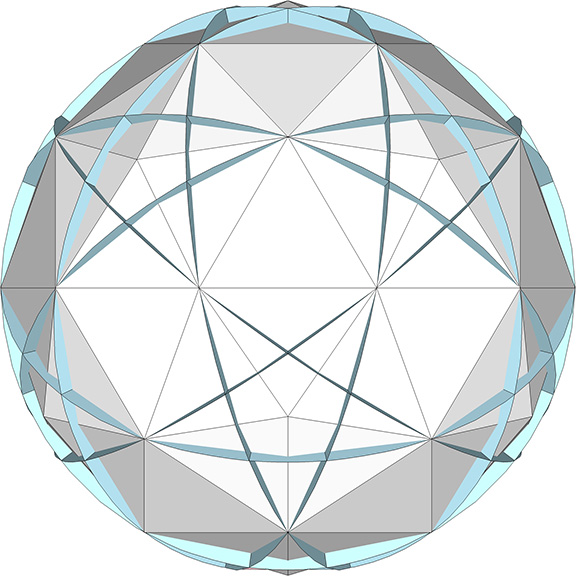
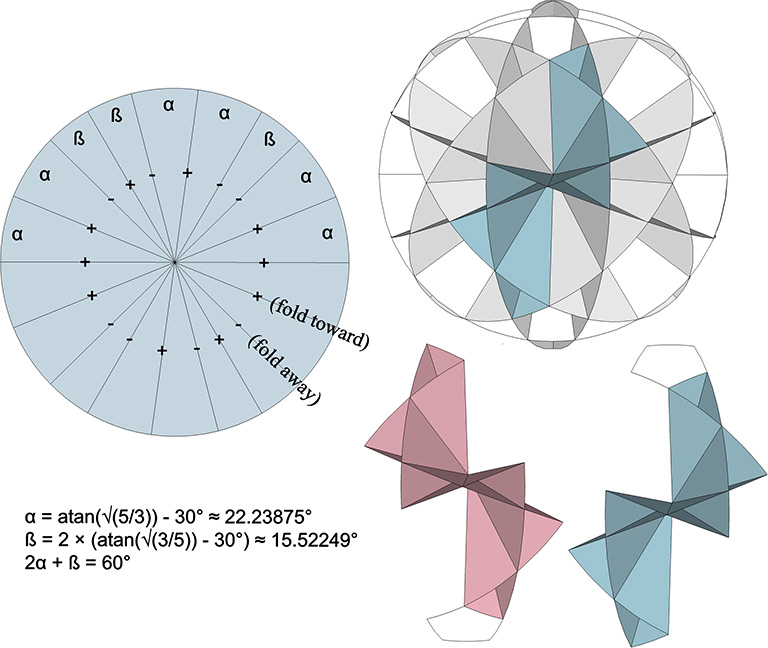
The 10 great circles of the icosahedron describe 60 identical triangles on the surface of the sphere. The central angles are: atan(√(5/3)) – 30° ≈ 22.23875°; 2×atan(√(3/5)) – 30° ≈ 15.52249°. Note that the two angles add to precisely 60°. The central angles are laid out on each of the ten great great circle disks, which are then folded to produce 10 chains (5 positive and 5 negative) each consisting of six identical edge-bonded tetrahedra. When properly arranged, the tetrahedra define between them the additional twelve pentagons and twenty hexagons in the pattern illustrated.
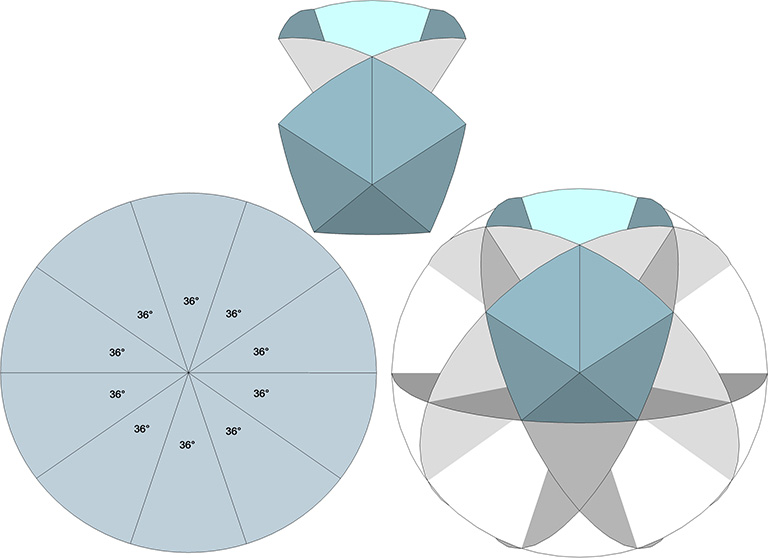
The 6 great circles of the icosahedron are the geodesics described by the regular icosahedron’s 6 vertex-to-vertex axes of spin. They describe the spherical icosidodecahedron with its twelve identical pentagons and twenty triangles. The icosidodecahedon is the vertex-truncated regular icosahedron, and is also the shape of the 30-strut spherical tensegrity that reduces to the icosahedron (see Tensegrity). The central angles, all 36°, and are laid out on each of the six great great circle disks, which are then folded to produce six pentagonal bow ties. When properly arranged, the pentagons define between them the additional twenty triangles in the pattern illustrated.