Formation and Distribution of Nuclei in Radial Close-Packing of Spheres

Greg Frederick

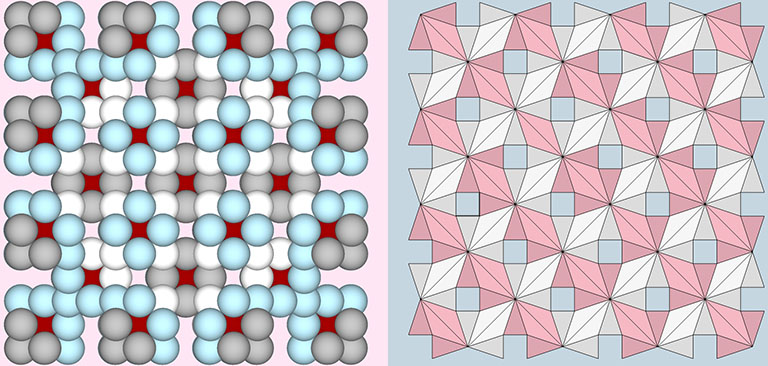
The third shell of radially close-packed, unit-radius spheres around a common nucleus consists of 92 spheres, a number that Buckminster Fuller did not consider coincidental. (See: Close-Packing of Spheres.) The Periodic Table of Elements, with its 92 stable elements ranging from hydrogen to uranium is after all the close packing of neutrons and protons. Also intriguing is the emergence, in the third shell, of eight new potential nuclei at the centers of the eight triangular faces.

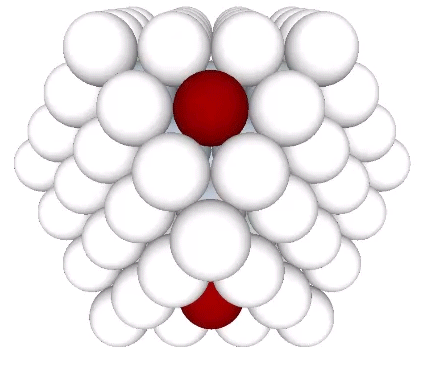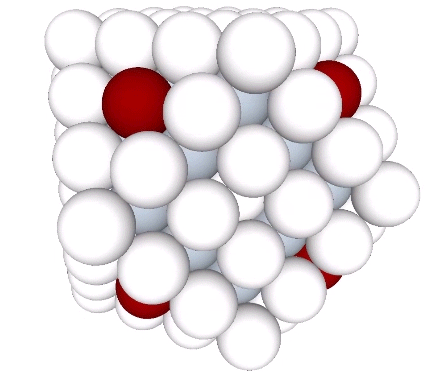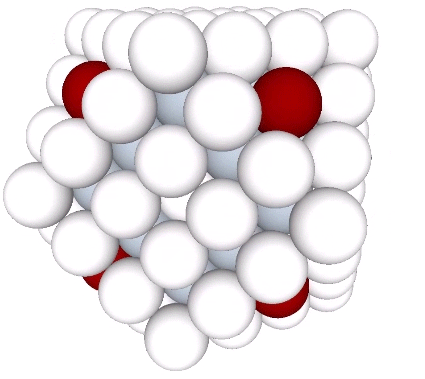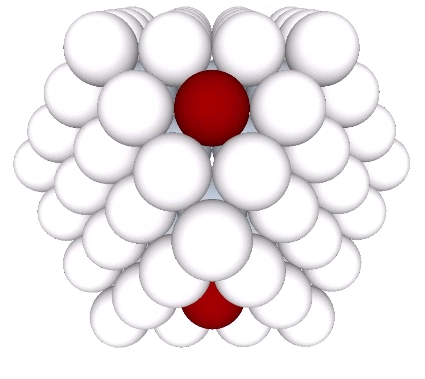
Three shells of radially close-packed spheres around a nucleus, forming a VE with eight potential nuclei (red) at the centers of its eight triangular facets.
Eight unique nuclei emerge in the third shell of radially close-packed spheres. The third shell contains 92 spheres, suggesting a correspondence to the number of stable atoms in the periodic table of elements.

If these eight spheres are added to the second shell’s 42 spheres, they constitute the corners of the first nucleated cube to emerge in the isotropic vector matrix.

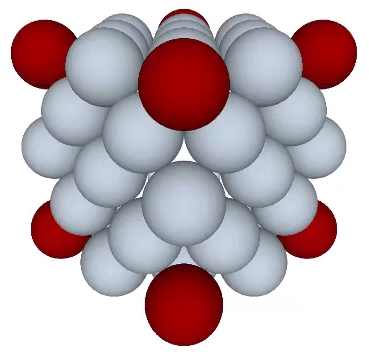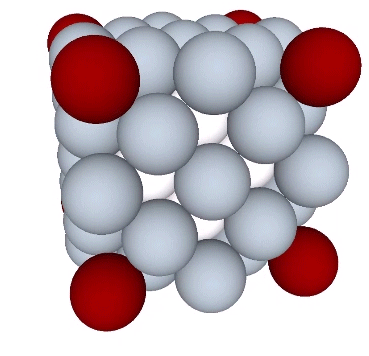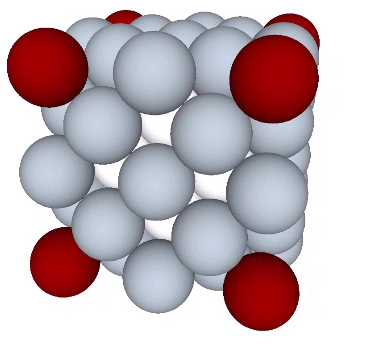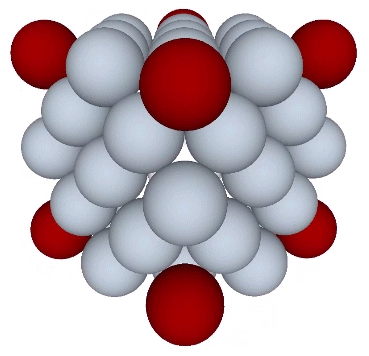
Cube constructed of two shells of radially close-packed spheres and the eight potential nuclei (red) from the third shell.
The eight new nuclei that emerge in the third shell of the isostropic vector matrix are positioned at the corners of the first nucleated cube.

And if each is given its own shell of 12 spheres, we can see clearly their nuclear character.

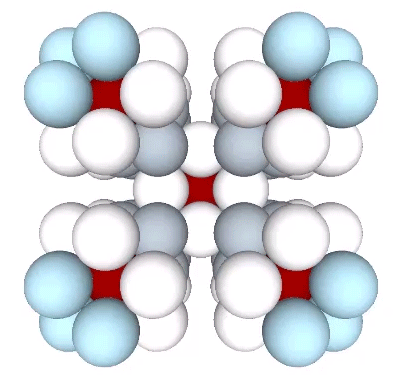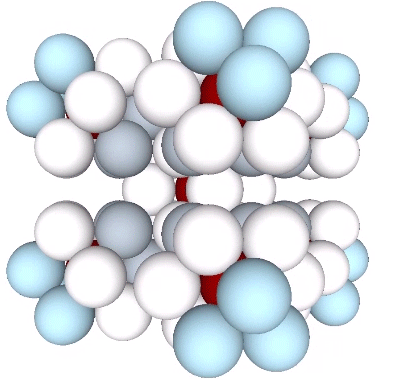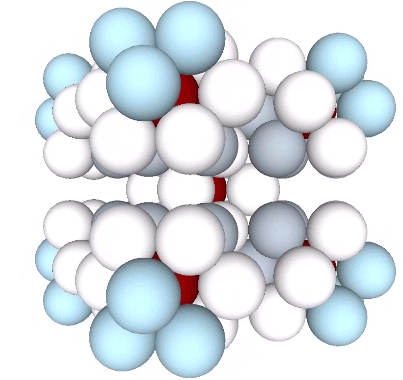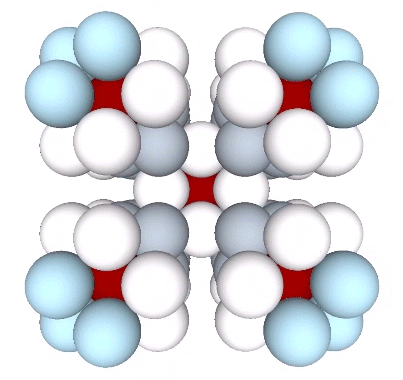
Twelve-sphere shells enclosing each of eight nuclei distributed around the central nucleus.
The first nine nuclei to emerge in the isotropic vector matrix along with their 12-sphere shells. Colors identify shell number.

In the close-packed spheres model of the isostropic vector matrix, every sphere is surrounded by twelve others. Whether or not a given sphere in the close-packed array is a nucleus is an arbitrary choice. But the selection of one determines the the regular distribution of all the others.

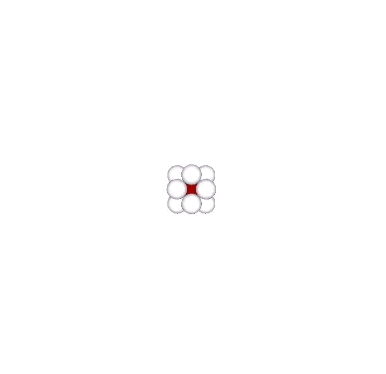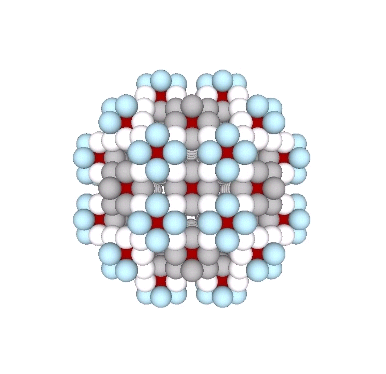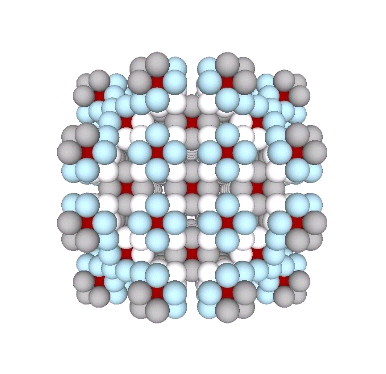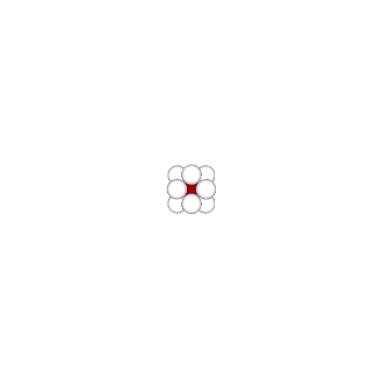
Stop-frame animation of emergent nuclei and their twelve-sphere shells for seven layers of radially close-packed spheres.
Unique nuclei and their shells, as distributed in radially concentric layers 0 through 7 of isotropic vector matrix.

Connecting the centers of unique nuclei forms a grid of rhombic dodecahedra, fourteen around one, not twelve, as might be expected.

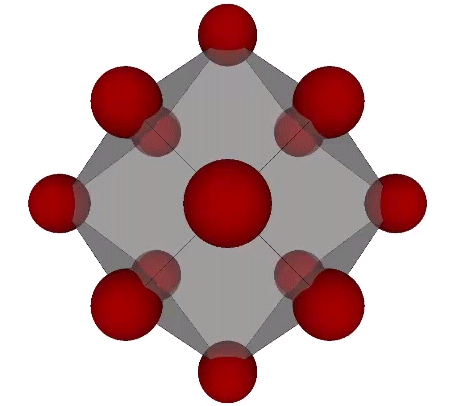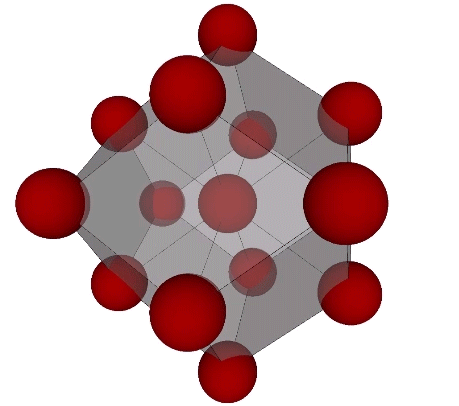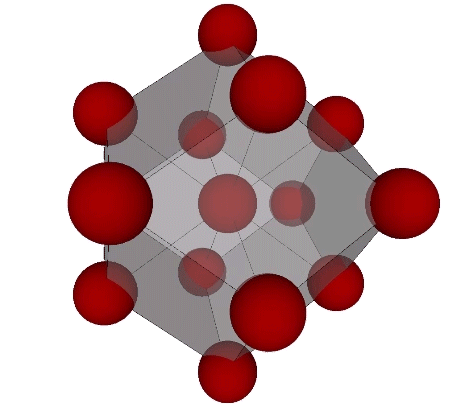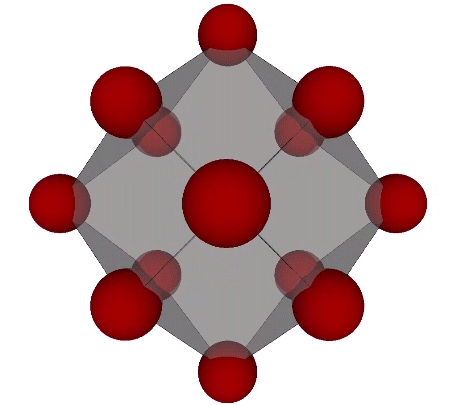
Fourteen unit-diameter nuclei (red spheres) centered on the vertices of a nucleated 3F rhombic dodecahedron.
Vectors connecting unique nuclei in the isotropic vector matrix define a rhombic dodecahedron

Spherical domains close-pack as rhombic dodecahedra, twelve around one. Nuclear domains close pack like soap bubbles and foams, fourteen around one, and their domain is identical with the solution to the Kelvin problem: How can space be partitioned into cells of equal volume with the least area of surface between them? Fuller noted that the Kelvin truncated octahedron, initially proposed as the solution to the Kelvin problem, encloses nuclear domains.

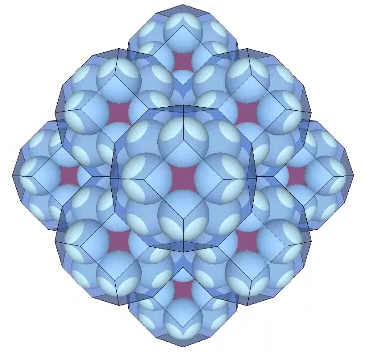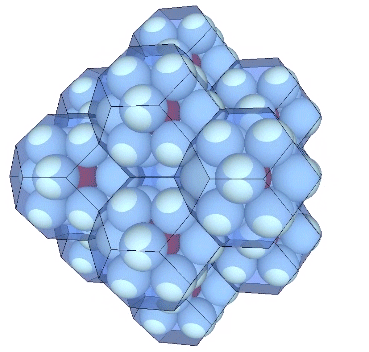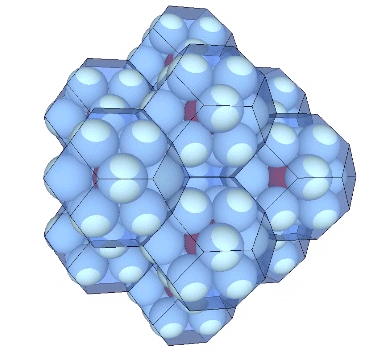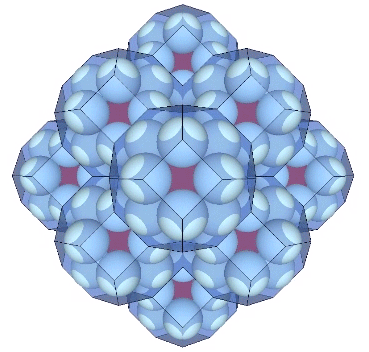
Fifteen transparent radially face-bonded Kelvin tetrakaidecahedra each enclosing a nucleus (red sphere) and its twelve-sphere shell (white spheres).
Unique nuclei and their 12-sphere shells are distributed in the isotropic vector matrix as Kelvin tetrakaidecahedra (aka truncated octahedra).

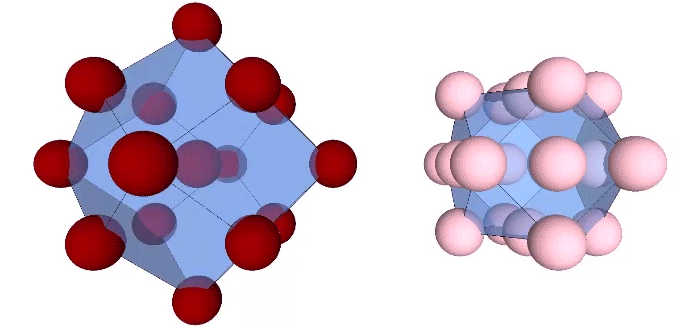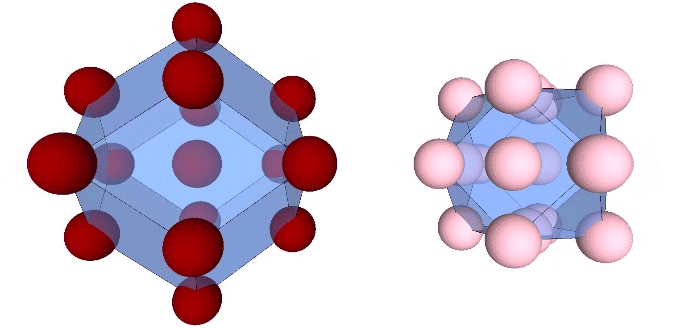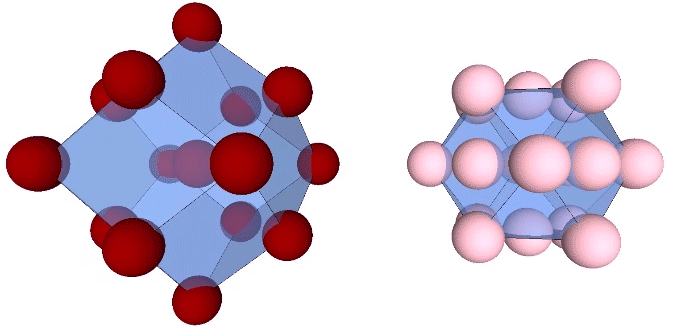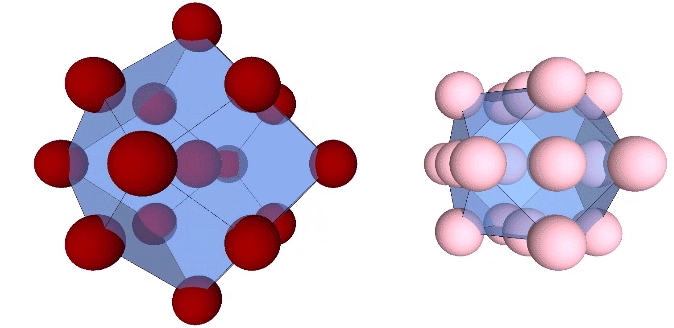
Presently, the best solution to the Kelvin problem is the Weaire-Phelan matrix consisting of Tetrakaidecahedron and Pyritohedron of equal volume. The distribution of nuclei in the isotropic vector matrix coincides beautifully with the Weaire-Phelan matrix, with unique nuclei (shown in red in the figure below) enclosed by pyritohedra, and nuclei whose shells are shared with their surrounding nuclei (shown as pink in the figure below) are enclosed by pairs of tetrakaidecahedra.

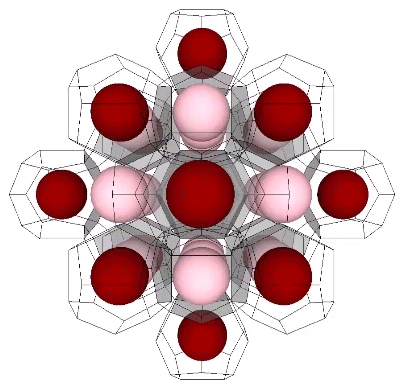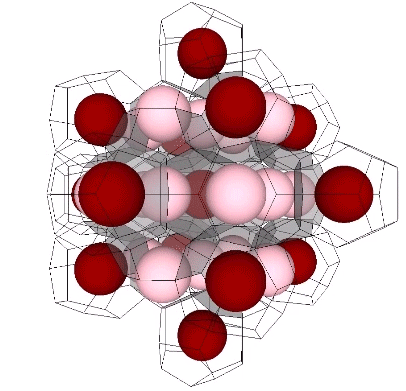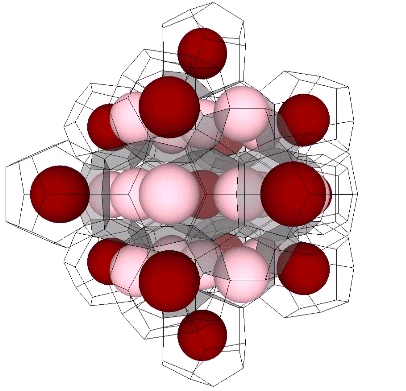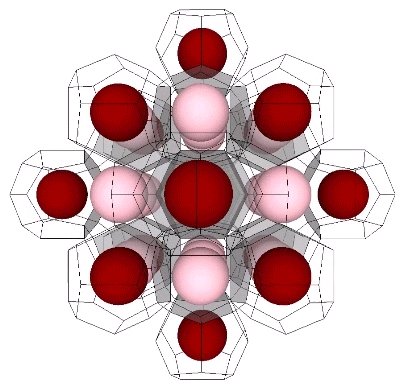
Wireframe Weaire-Phelan matrix aligned with the radial distribution of fifteen unique (red spheres) and eighteen non-unique nuclei (pink spheres).
The Weaire-Phelan matrix isolates unique nuclei (red) inside pyritohedra. The surrounding matrix of paired tetrakaidecahedra encloses the nuclei whose shells are shared with surrounding nuclei (pink).

This distribution is perhaps easier to conceptualize if we separate out the pyritohedra and the tetrakaidecahedra.

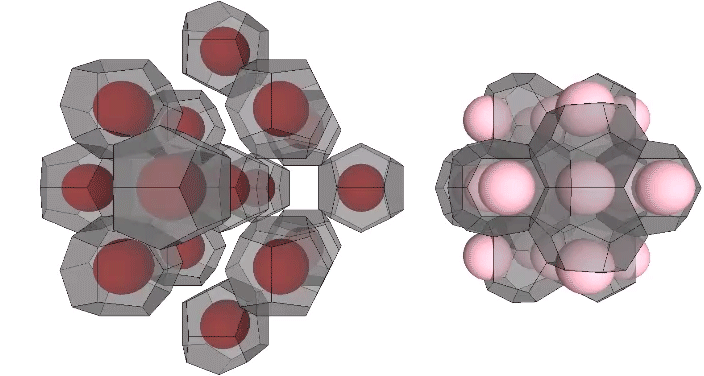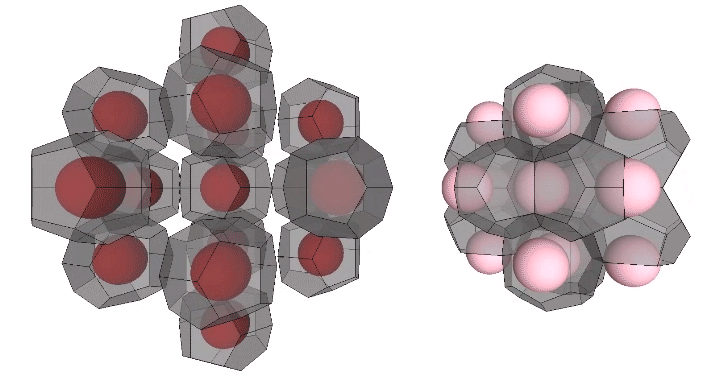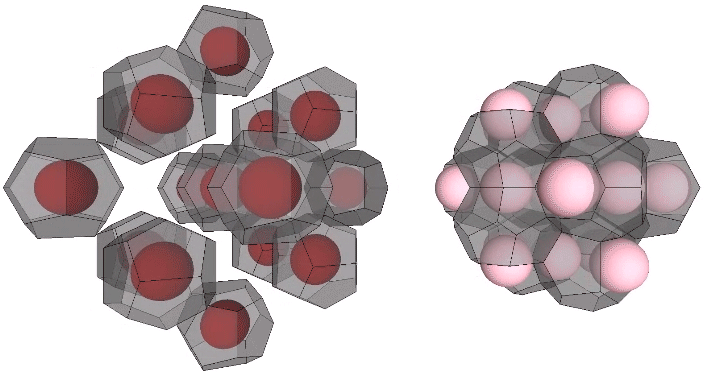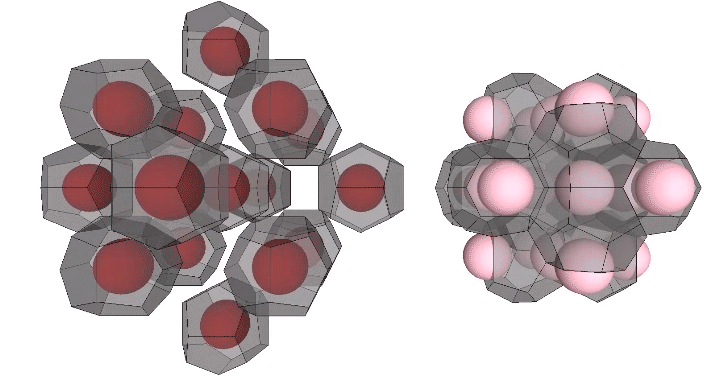
Transparent pyritohedra (left) enclosing fifteen radially distributed nuclei (red spheres). Transparent tetrakaidecahedra (right) partially enclosing eighteen radially distributed non-unique nuclei (pink spheres).
The Weaire-Phelan matrix separated into pyritohedra (left), and tetrakaidecahedra (right), demonstrating their distribution with respect to the unique nuclei (left) and non-unique nuclei (right) in the isotropic vector matrix.

As noted earlier, unique nuclei are distributed on a grid of rhombic dodecahedra. The nuclei whose shells are shared with surrounding nuclei, however, are distributed on a grid of vector equilibria.

Radially distributed nuclei (red spheres) at the vertices of transparent 3F rhombic dodecahedron (left). Radially distributed non-unique nuclei (pink spheres) at the vertices of a transparent 2F VE (right).
Unique nuclei (left) and non-unique nuclei (right) are distributed in the isotropic vector matrix as rhombic dodecahedra and VEs respectively.

If the non-unique nuclei are removed from the matrix, they leave holes that run through the matrix along orthogonal paths. These are likely the same holes seen in the icosahedron phases of the jitterbug.

Schematic of close-packed nuclei and their twelve-sphere shells (left), and of close packed Jessen orthogonal icosahedra (right), both with orthogonal voids tunneling through the matrix.
Left: Close-packed spheres of isotropic vector matrix showing nuclei (red) and their shells, with non-unique nuclei removed; Right: Vector model of the isotropic vector matrix at the Jessen orthogonal icosahedron phase of jitterbug, exactly midway through the transformation between VE and octahedron.

Leave a comment