“Though of equal energy potential or latent content, the [A and B quanta modules] are two different systems of unique energy-behavior containment. [The A quanta module] is circumferentially embracing, energy-impounding, integratively finite, and nucleation-conserving. [The B quanta module] is definitively disintegrative and nuclearly exportive. A is outside-inwardly introvertive. B is outside-outwardly extrovertive.”
—R. Buckminster Fuller, Synergetics, 921.40
The A and B quanta modules constitute the lowest common denominator of polyhedral systems, just as the Basic Disequilibrium LCD Triangle constitutes the lowest common denominator (LCD) of the sphere’s surface.
Construction of the A and B Quanta Modules
To construct the A quanta module, the regular tetrahedron is divided into four identical quarter-tetrahedra whose apexes converge at its center of volume.
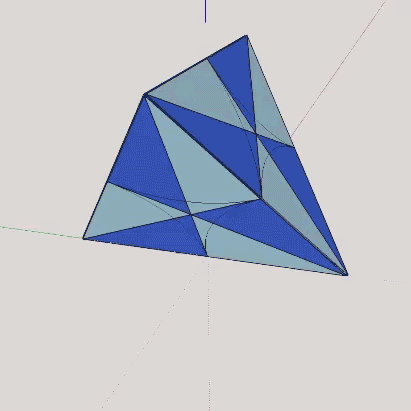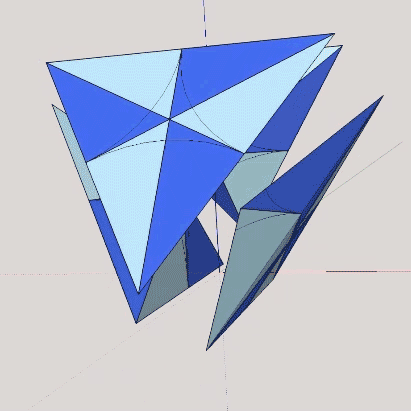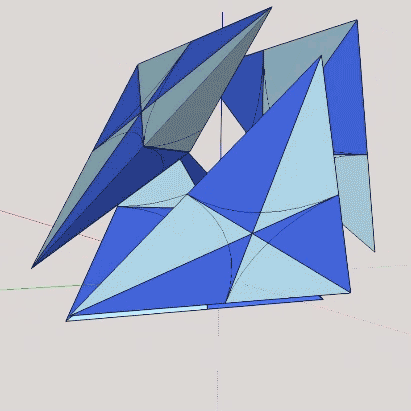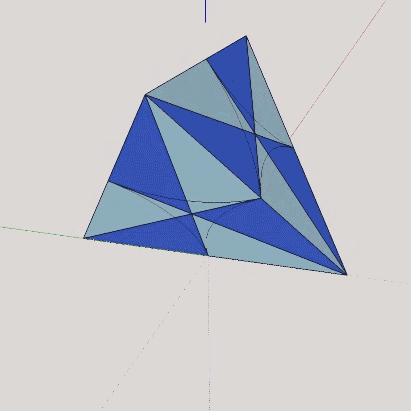
The quarter-tetrahedra are further subdivided into six identical irregular tetrahedra—three positive and three negative (inside-out)—by describing lines that are perpendicular bisectors from each vertex to their opposite edge. These are the A quanta modules.

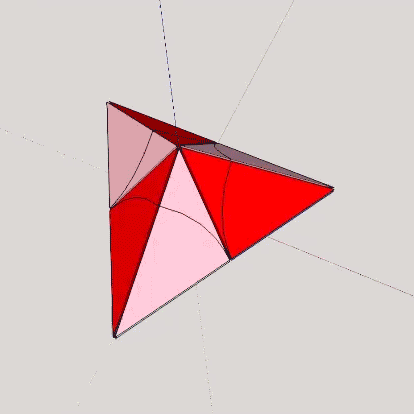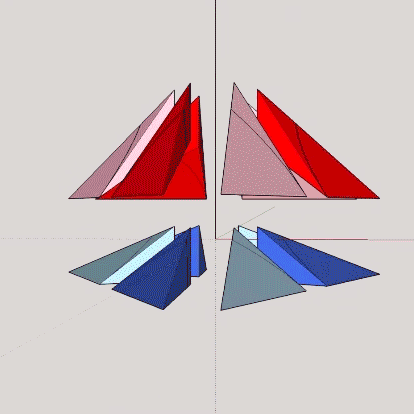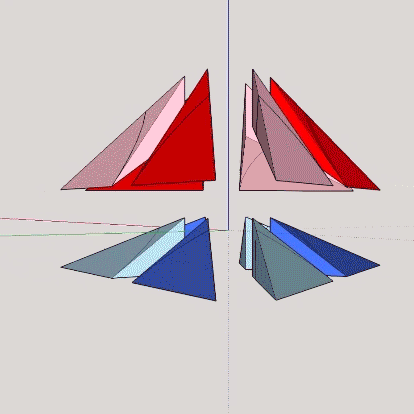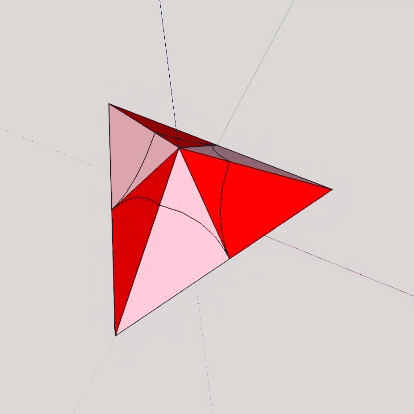
The regular octahedron has a volume equivalent to that of four regular tetrahedra. The octahedron may be subdivided symmetrically into eight equal eighth-octahedra by planes going through the three axes connecting its six vertexes.

The quarter-tetrahedron and the eighth-octahedron each have the same equilateral triangular base. With their bases congruent we can superimpose the eighth-octahedron over the quarter-tetrahedron. We find, operationally, that the height of the eighth-octahedron is exactly twice that of the quarter-tetrahedron. So, by removing the quarter-tetrahedron and subdividing as before, we are left with six uniformly symmetrical components—three positive, and three negative (inside-out)—with the same volume as the A quanta module. These are the B quanta modules.
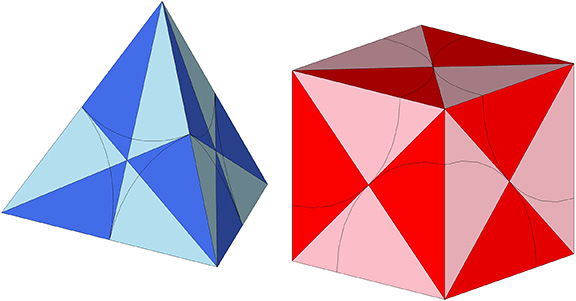
The A and B quanta modules each have the volume of 1/24th that of the regular tetrahedron. Combinations of the two produce rational, whole-number volumes for all the regular polyhedra that appear in the isotropic vector matrix.
Dimensions of the A and B Quanta Modules
The A Quanta Module unfolds into a scalene triangle; all its angles are different, and all are less than 90°. Two of the fold lines are perpendicular to the triangle’s sides, thus producing the four right angles of the folded module. The A quanta module triangle may be unique in that neither of its two perpendiculars bisect the edges that they intersect. It has three internal folds and no internal triangle. It drops its perpendiculars in such a manner that there are only three external edge increments, which divide the perimeter into six increments of three pairs. The folds progress linearly, in a spiral.
The unfolded A quanta module may be the only scalene triangle with these properties, and may be the only scalene triangle that can be folded into a tetrahedron.
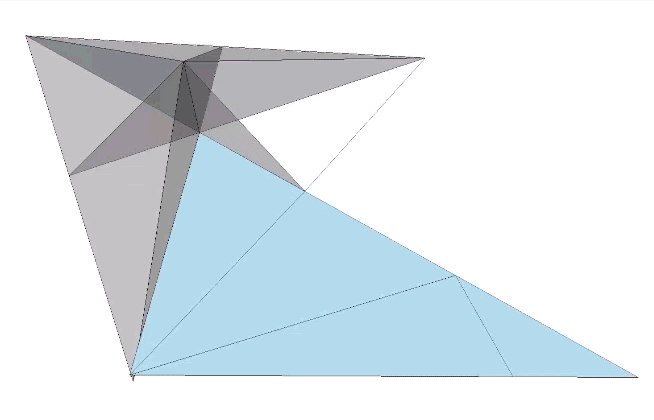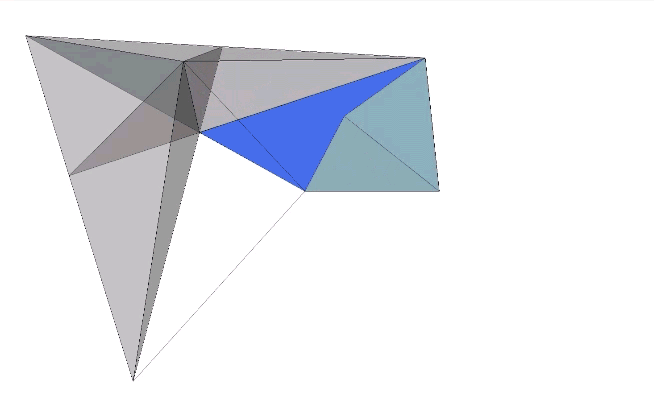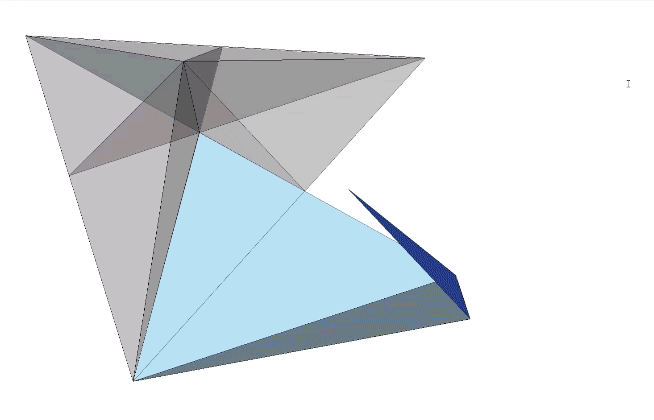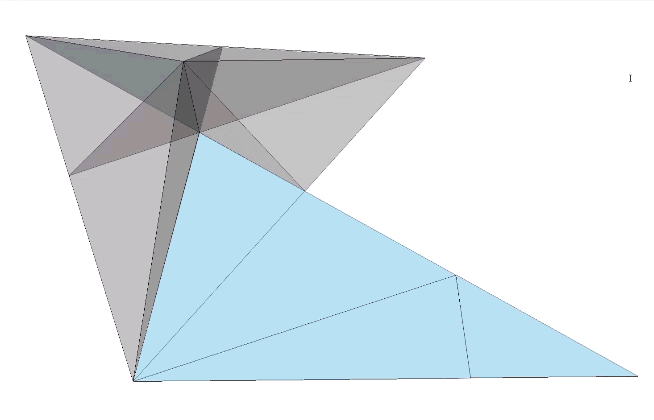
The plane net of the unfolded A quanta module in the following illustration will fold along the fold lines AB, AD and CD to produce either a positive or a negative A quanta module. The vertex D is at the center of the tetrahedron from the A quanta module is derived, A is at the vertex, B is at mid-edge, and C is at mid-face.
Its six edges have the following lengths, with r taken as unity:
- AC = r√3/3;
- CB = r√3/6;
- BD = r√2/4;
- AB = r/2;
- AD = r√6/4;
- DC = r√6/12;
Given the following angles:
- a = atan(√2) ≈ 54.735610°;
- b = atan(√2/2) ≈ 35.254390°;
- c = atan(√2/4) ≈ 19.471221°;
- 2b = atan(2√2) ≈ 70.528779°;
the vertices are: A(30°,b,c); B(90°,90°,b); C(90°,90°,60°); and D(a,2b,a).
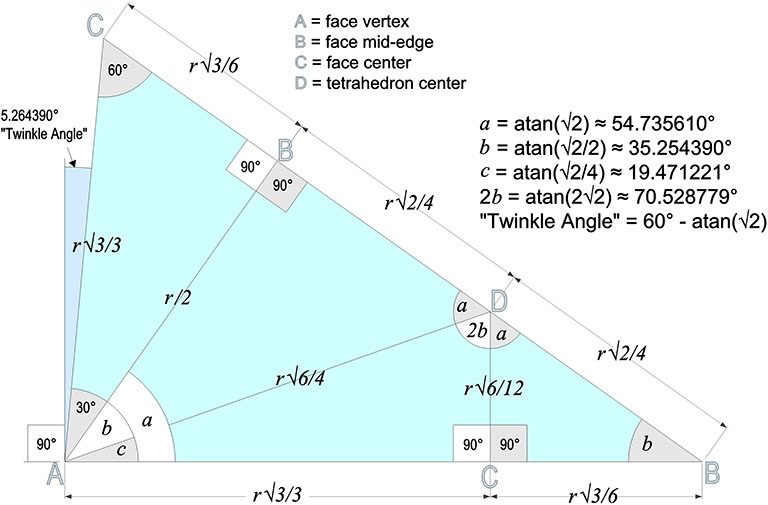
The faces of an A quanta module unfold to form a triangle with 84.73560°as its largest angle. This is 5.264390° less than a right angle, which is known as the “Twinkle Angle” in synergetics, and relates to the unfolded A quanta module bearing a striking resemblance to the Basic Disequilibrium LCD Triangle. Fuller proposed that the two were, in fact, the same triangle; that is, the basic disequilibrium LCD triangle is the spherical version of the A quanta module triangle. Supporting this proposition is the fact that all of the LCD triangle’s central angles are paired in the same way the edge lengths are paired in the A module triangle. So, if it were possible to fold a spherical triangle into a tetrahedron, the basic disequilibrium LCD triangle would have all the appropriate dimensions.
Trigonometric expressions for the Twinkle Angle include: 60° – arctan(√2); 90° – arctan(3√3 + 4√2)); arccot(3√3 + 4√2), and; arctan((4√2 – 3√3)/5).

The B quanta module cannot be unfolded into a single triangle. It can only be unfolded into an irregular polygon made up of four dissimilar triangles. The plane net of the unfolded B quanta module in the following illustration will fold along the fold lines BE, EA, and AC to produce either a positive or a negative B quanta module. The vertex E is at the center of the octahedron from which the B quanta module is derived; A is at the vertex; B is at mid-edge; and C is at face center.
Its six edges have the following lengths, with r given as 1/2 unity:
- AB = r/√2
- BD = r√2/4
- DE = r√6/12
- BE = r/2
- EA = r√2/2
- AD = r√6/4
Given the following angles:
- a = atan(√2) ≈ 54.735610°;
- b = atan(√2/2) ≈ 35.364390°;
- c = atan(√2/4) ≈ 19.471221°;
- d = atan(1/φ)/2 ≈ 15.858737°;
- b + 90° ≈ 125.264390°;
- 2a = c+90° ≈ 109.471221°
The vertices are: A(b, d, 45°); B(c, 90°, 90°); D(2a, a, b+90°), and E(b, 45°, a).

All of Fuller’s quanta modules come in pairs, positive and negative. One is the inside-out version of the other, which can be shown by opening three of their six edges and folding the three triangles’ hinged edges in the opposite direction until their edges come together again.
Energy Characteristics of the A and B Quanta Modules
Fuller describes the A quanta modules as energy-conserving and the B modules as energy-dispersing. This claim is backed up with a billiard table analogy—the triangles being the billiard table and the billiard balls being energy. A billiard table in the shape of an obtuse triangle would tend to direct the ball toward the pocket with the most acute angle. Whereas, on a billiard table in the shape of an equilateral triangle, no one pocket would attract more balls than another. A ball bouncing randomly around inside of the former would very quickly end up in the most acute corner’s pocket. In the latter it take would take longer, possibly forever, for the ball to reach a pocket. The A quanta modules combine to form the regular tetrahedron which, by the billiard table analogy, would tend to hold energy. The B modules, in addition to being made of highly obtuse triangles with sharply acute angles cannot combine with one another to form a single tetrahedron with energy-conserving proclivities. The B modules, therefore, tend to disperse rather than hold energy.
To underscore their energy characteristics, the A quanta modules are typically colored blue, and the B quanta modules are typically colored red. Blue signals energy-conserving, and red signals energy-dispersing. It is perhaps surprising that these characteristics often make intuitive sense when the quanta modules are combined into the shapes of the various polyhedra. For example, the tetrahedron, made entirely of blue A quanta modules, is stable, structural, and virtually indestructible. Whereas the cube, famously non-structural and unstable, is encased in red B quanta modules.