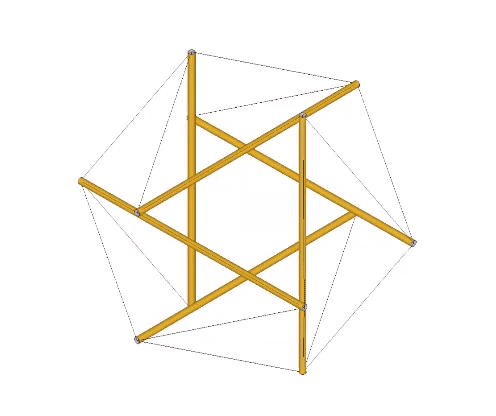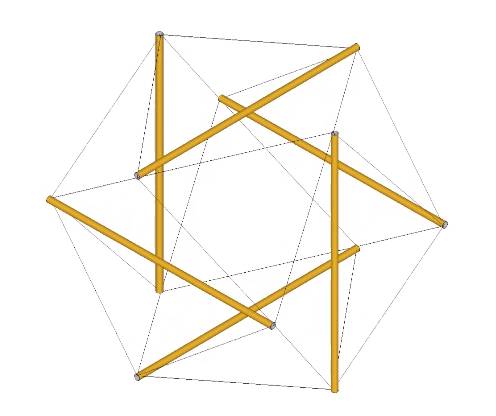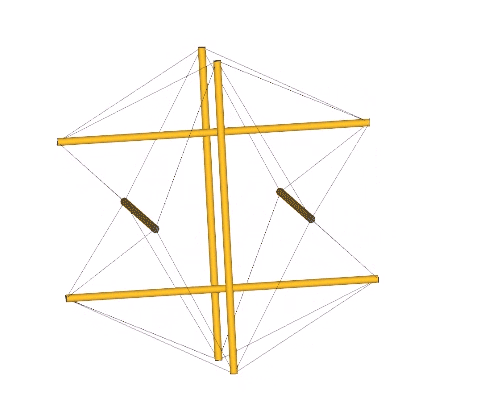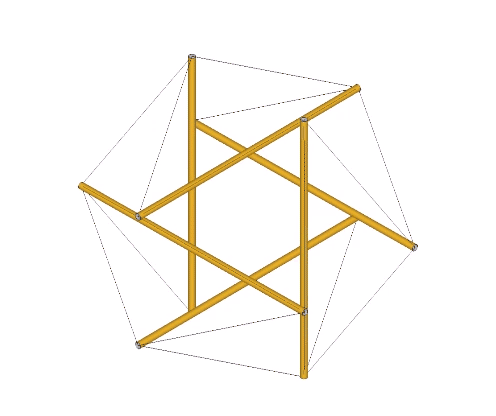The regular icosahedron has an irrational volume in both cubes and tetrahedra. Fuller accounted for this irrationality by noting that the icosahedron exists only as discrete shells and lattices; it does not close pack, either with itself or any other regular polyhedron to fill all space. Nature, therefore, had no need to assign it a volume commensurate with any of the other regular polyhedra.

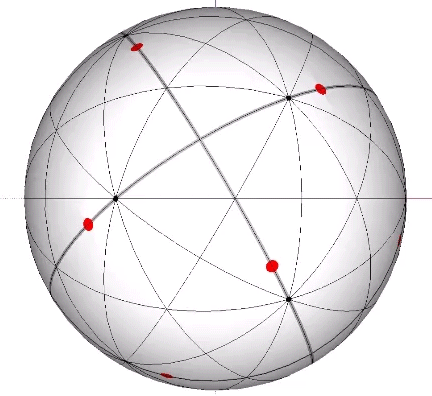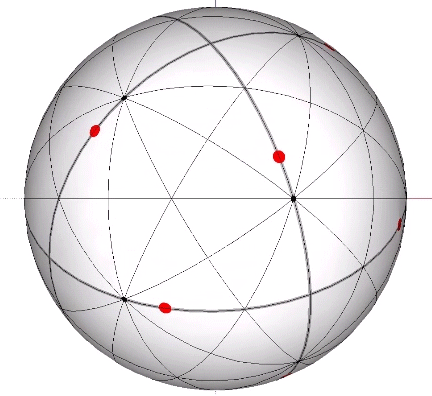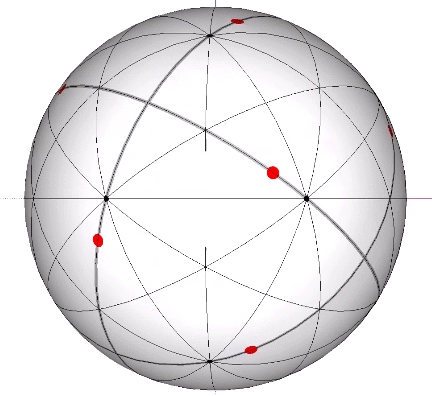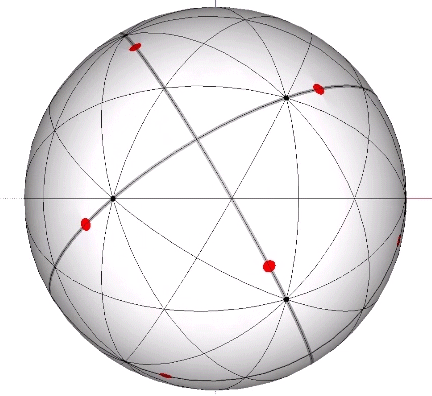
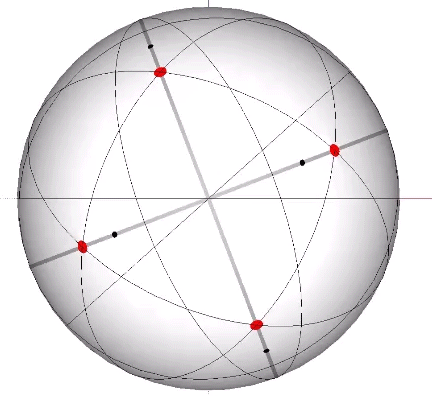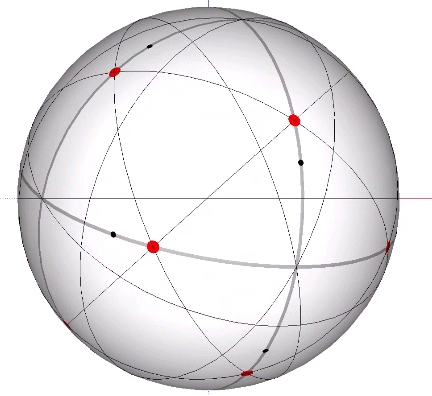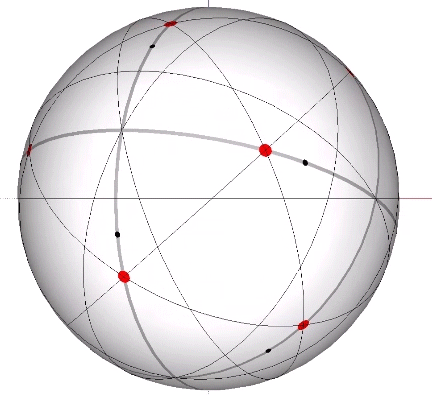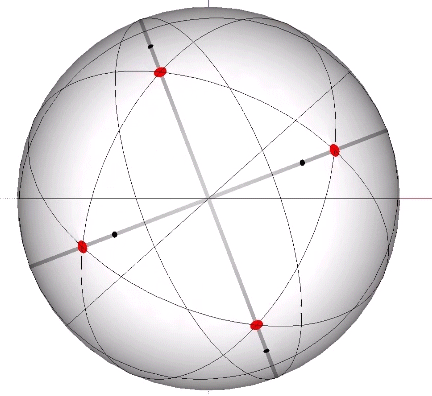
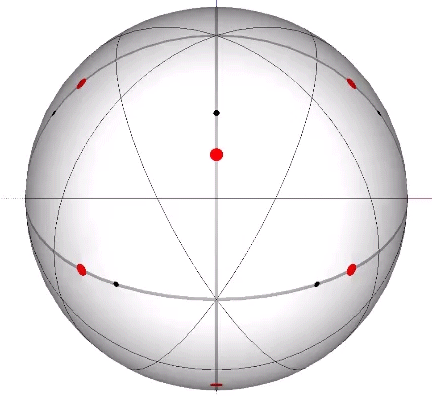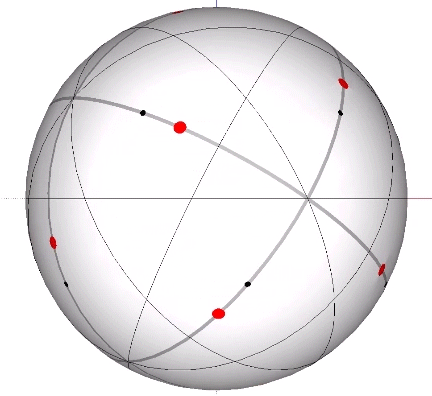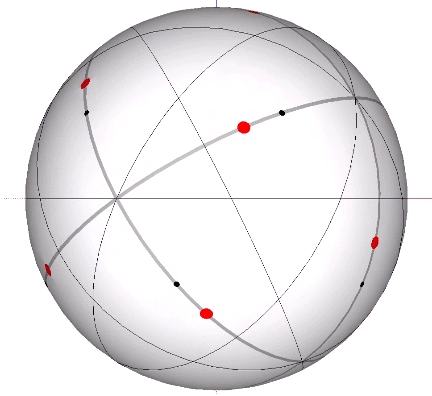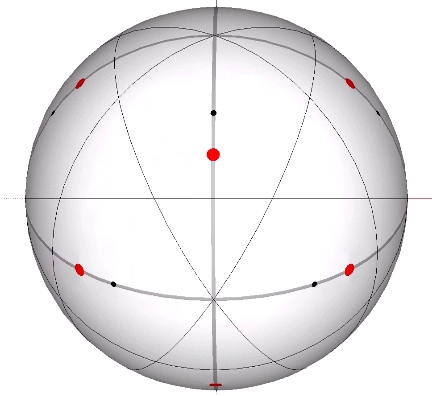
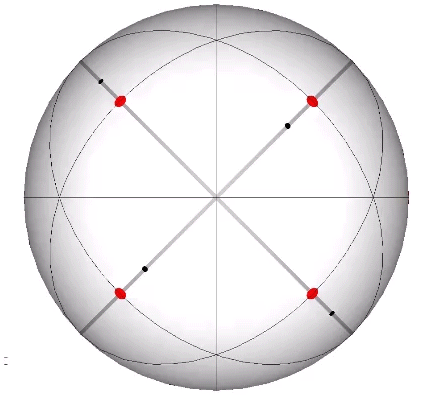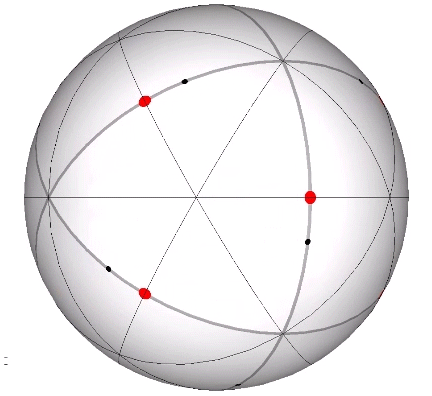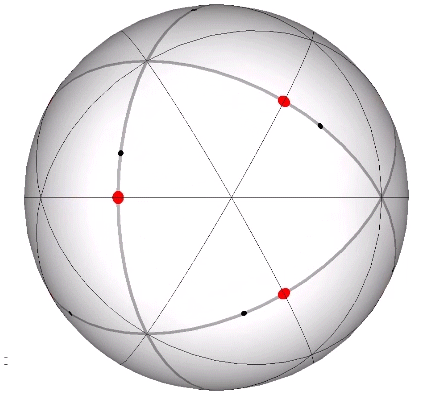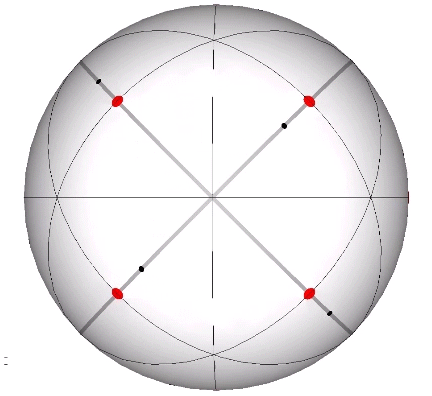
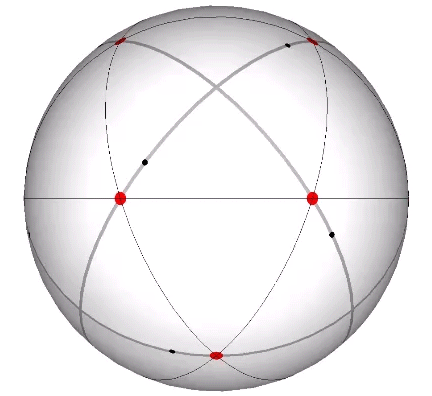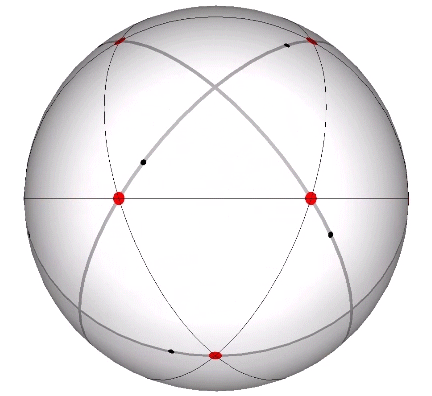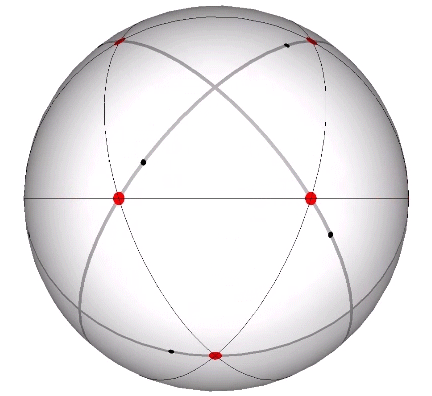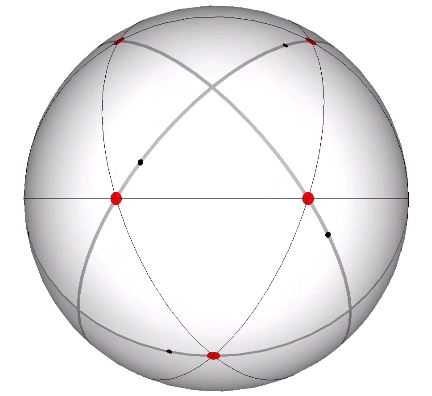
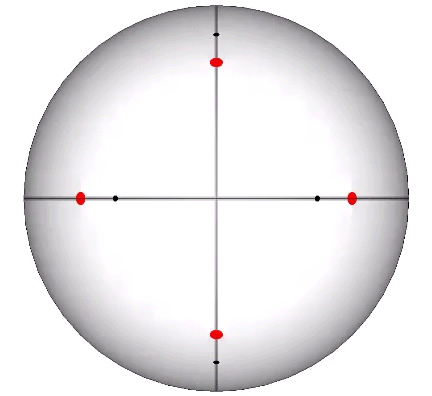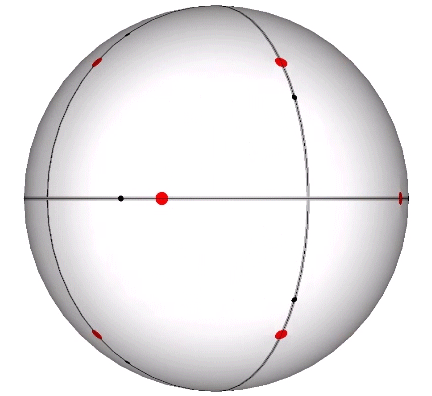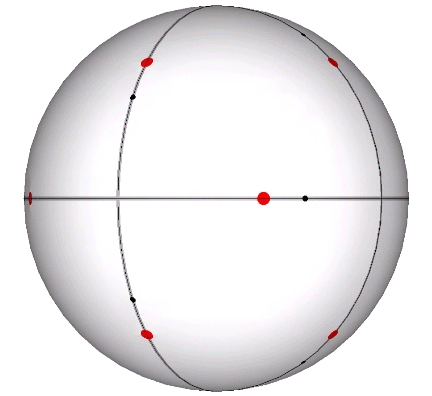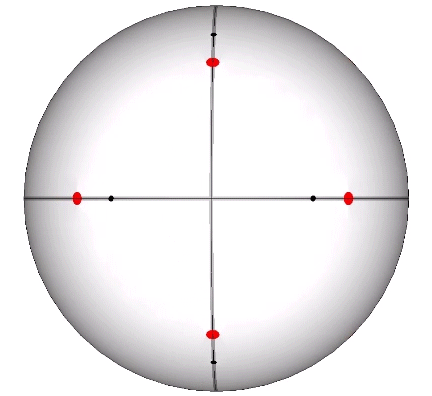
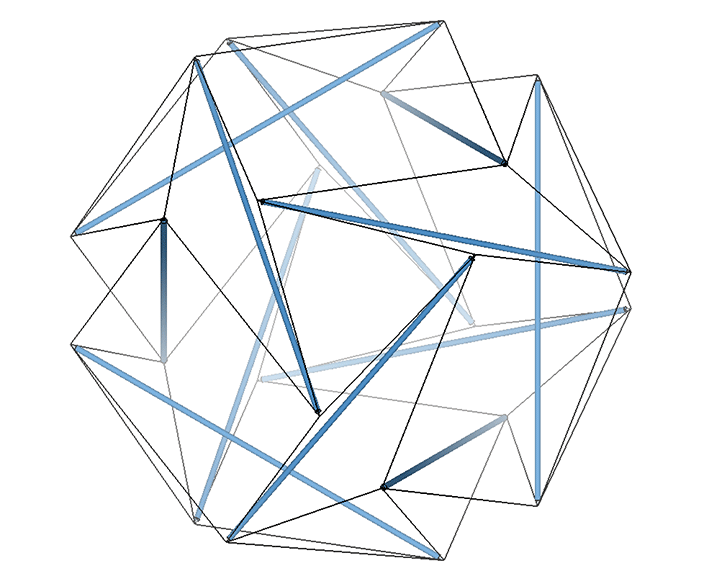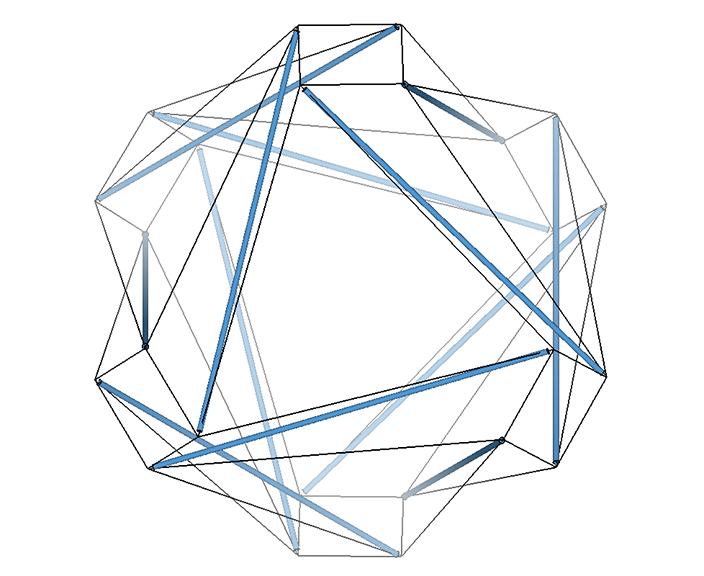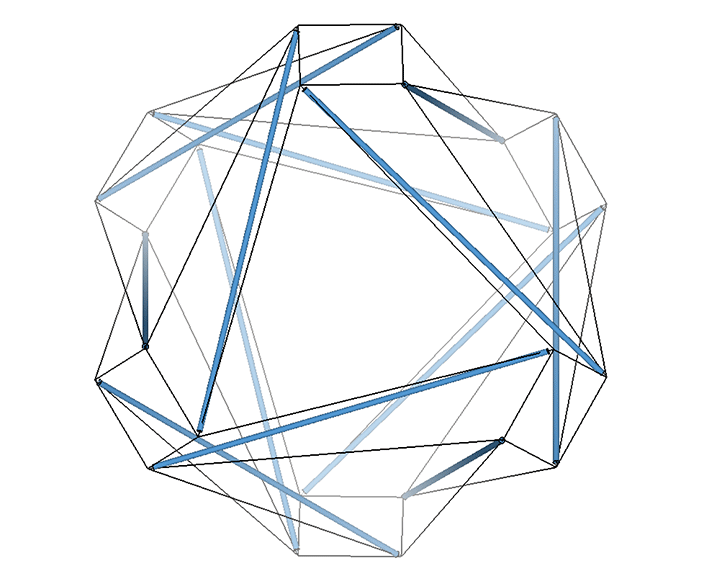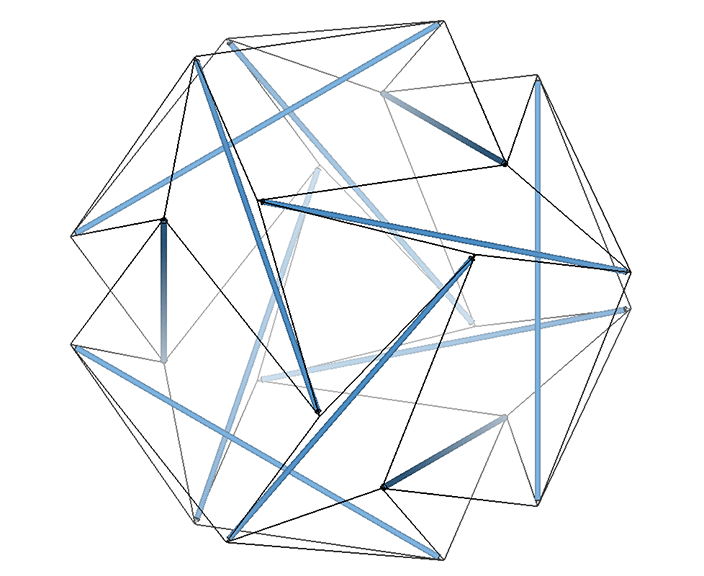
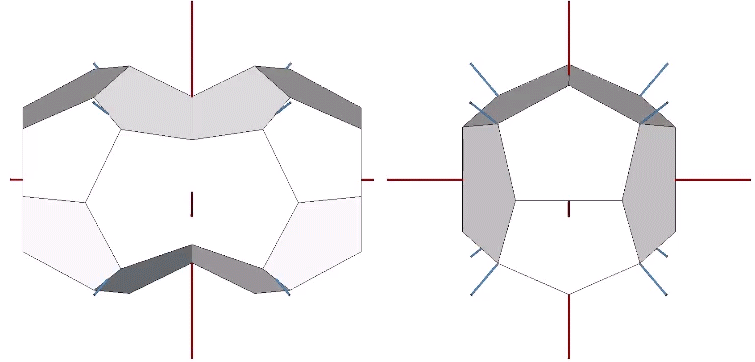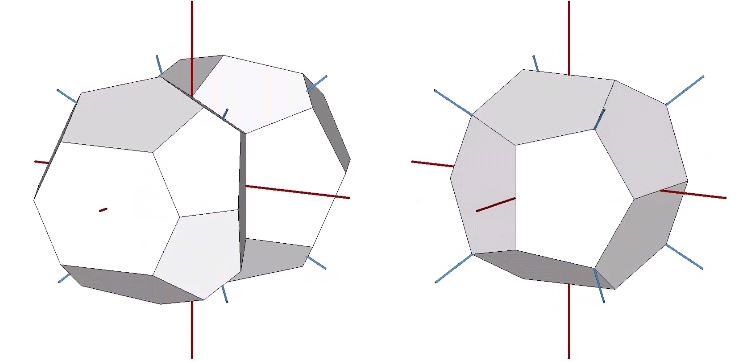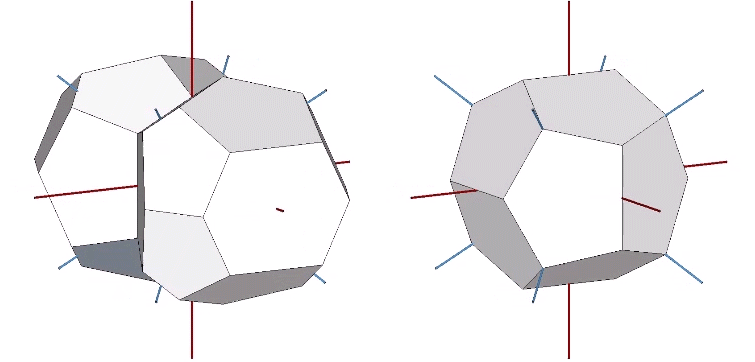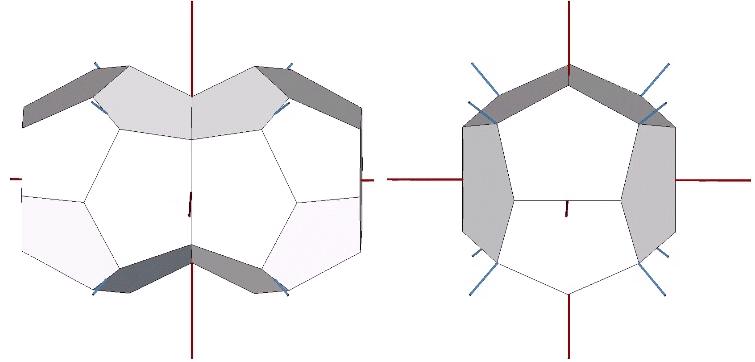
Its isolation is further reinforced by its axes of spin and the 31 great circles they describe. No great circle unique to the icosahedron passes through any point of contact with spheres radially close-packed in the isotropic vector matrix. Six of its great circles pass through no points of contact, including those between spheres arranged into icosahedral shells and lattices. This isolation suggests the icosahedron to be a model for potential energy, charge, and other holding patterns of energy.

The icosahedron of edge length a has the following properties:

• φ=golden ratio, (1+√5)/2)
• Face angles: all 60°
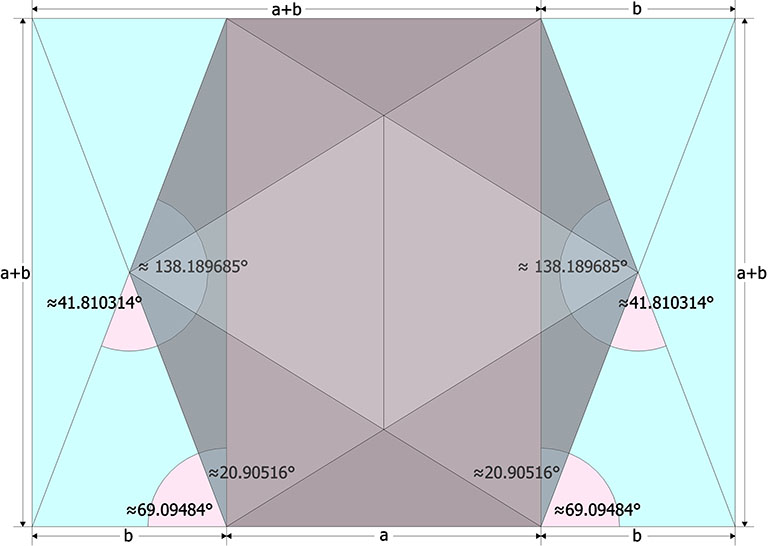
• Dihedral angle: acos(-√5/3) or 180°-asin(2/3) ≈ 138.189685°;
• Central angle of edge: atan(2) ≈ 63.434949°
• Volume (in tetrahedra): a³×5φ²√2 ≈ 18.512296
• Cubic volume: a³×5φ²/6 ≈ 2.18169499
• A and B quanta modules: n/a
• Surface area (in equilateral triangles): 20a²
• Surface area (in squares): 5a²√3
• In-sphere radius: a×φ²√3/6 ≈ 0.755761
• Mid-sphere radius: a×φ/2 ≈ 0.809017
• Circum-sphere radius: a×(√(φ+2))/2 ≈ 0.9510565

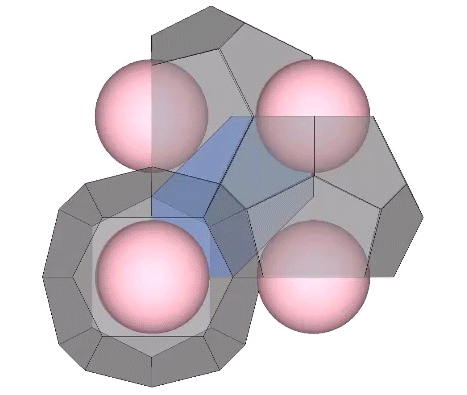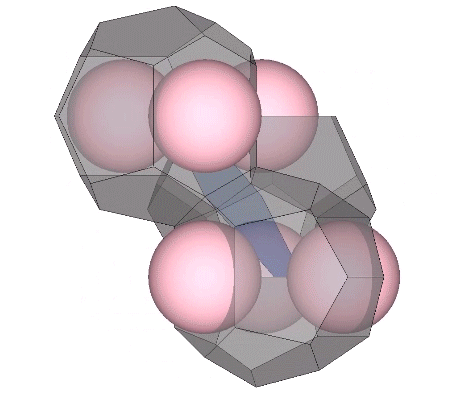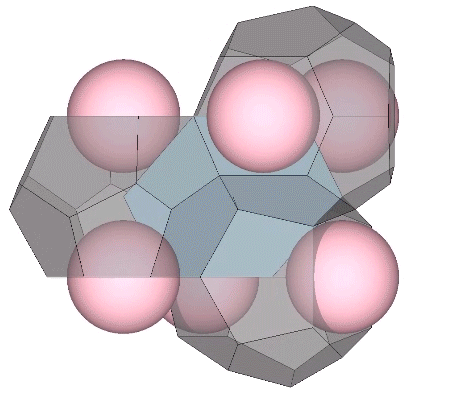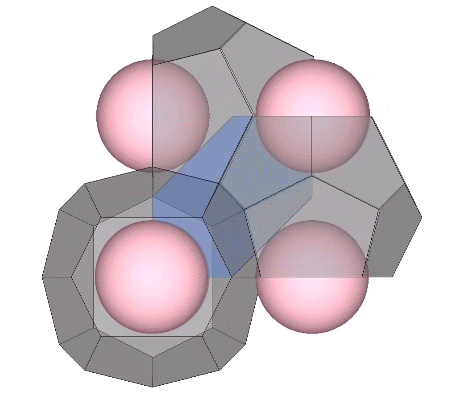
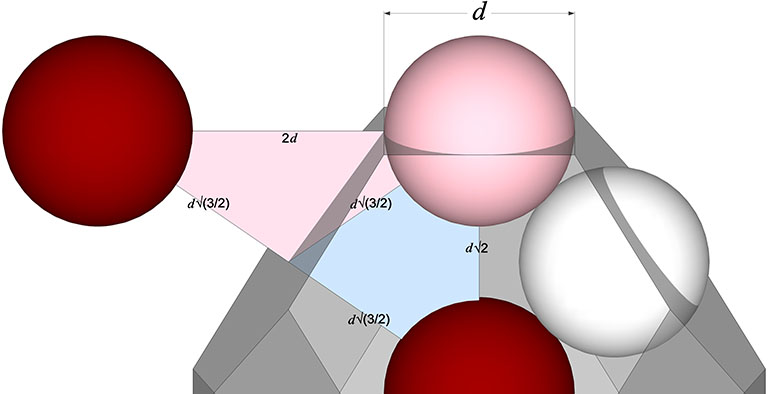
If the nucleus is removed from a radially close-packed cluster of 13 unit radius spheres (see Vector Equilibrium and the “VE”), the remaining 12 spheres naturally rearrange themselves into the stable configuration of the icosahedron.

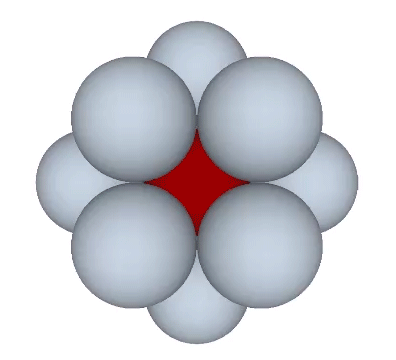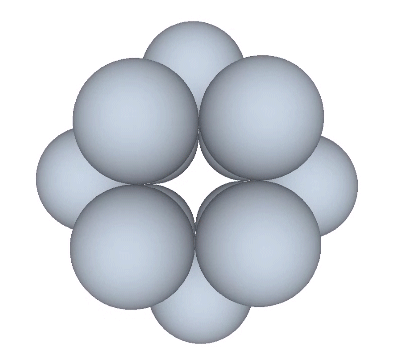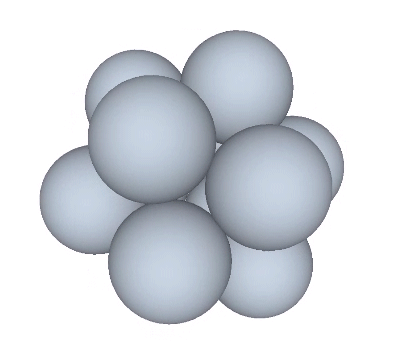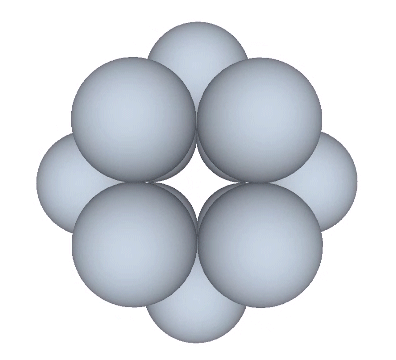
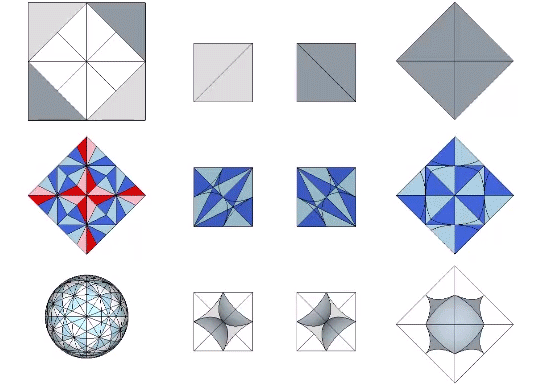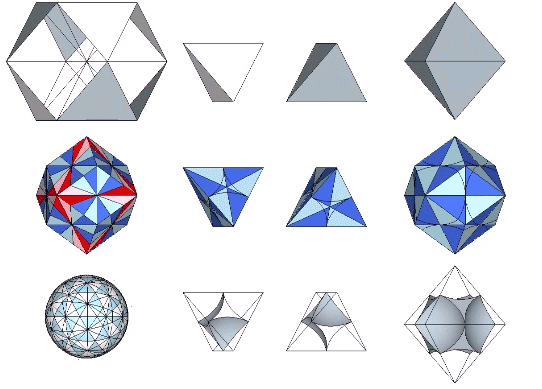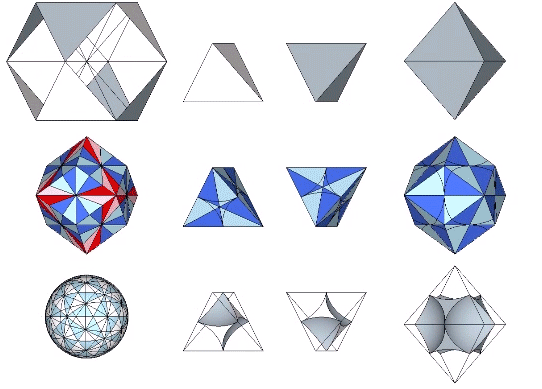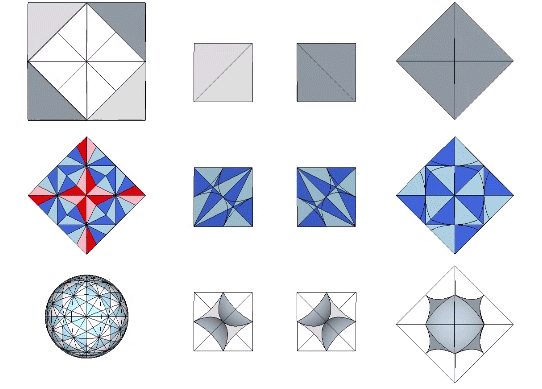
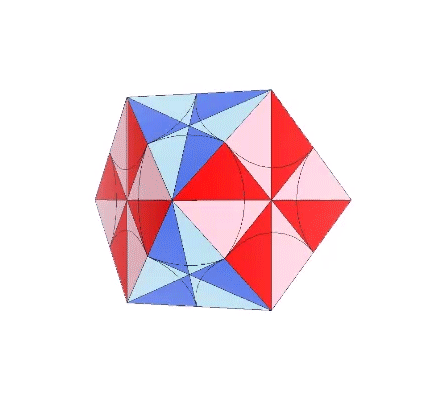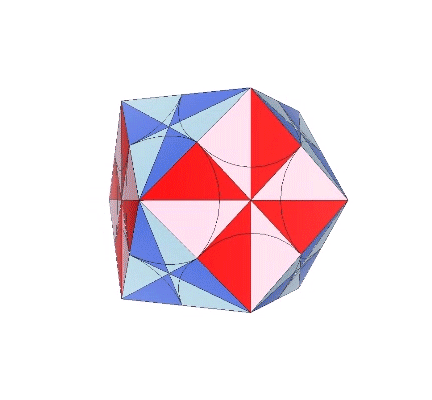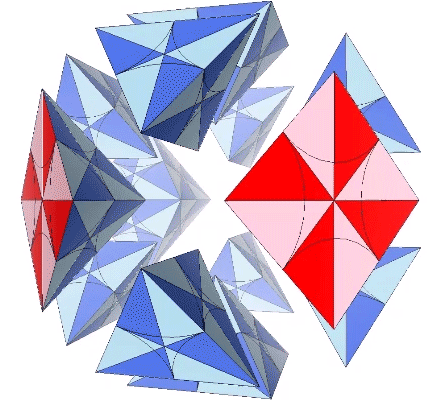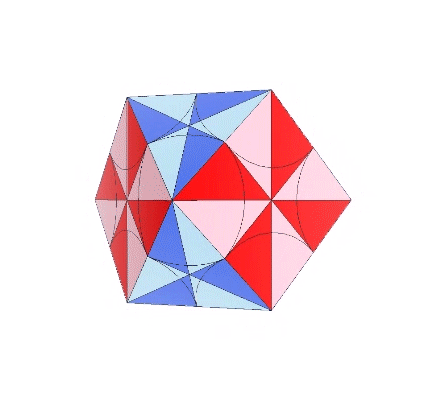
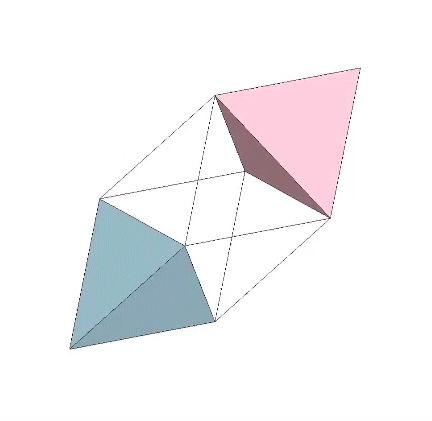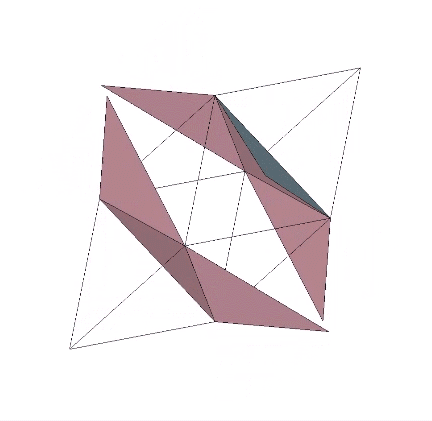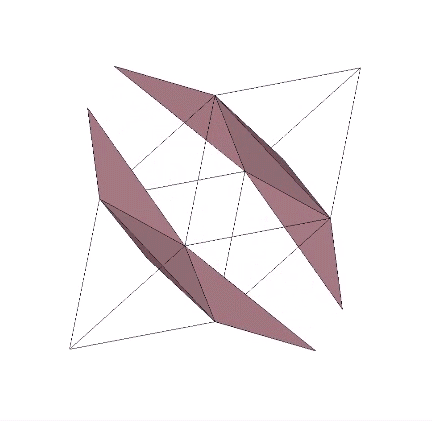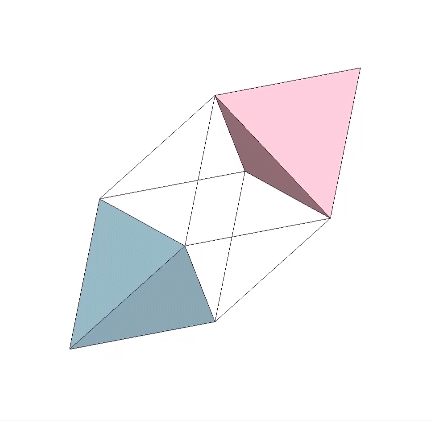
The icosahedron is famously derived from the golden ratio (φ), i.e., by connecting the vertices of three golden rectangles arranged orthogonally around a common center.

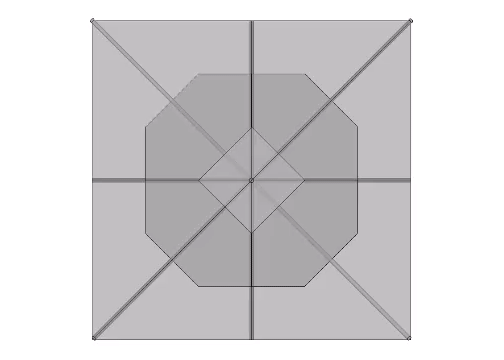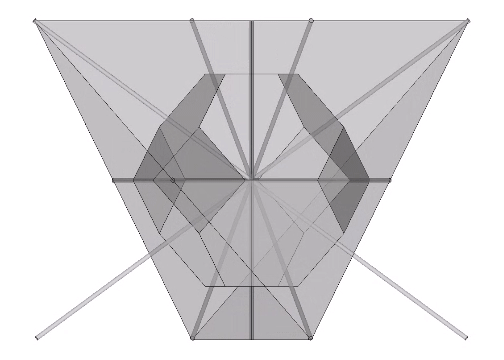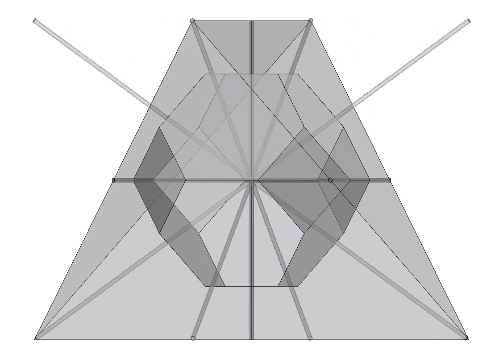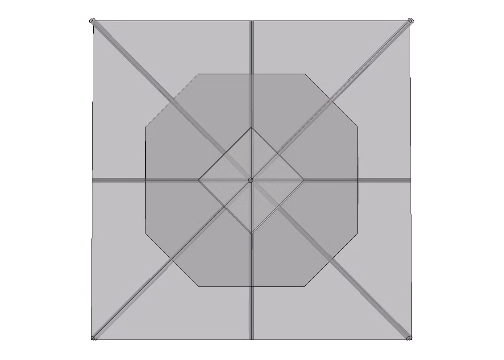
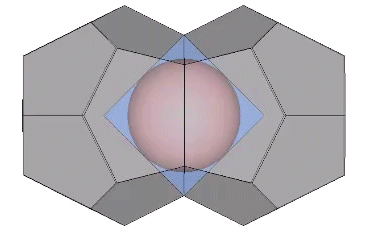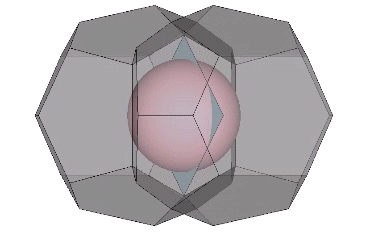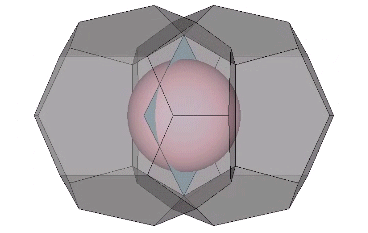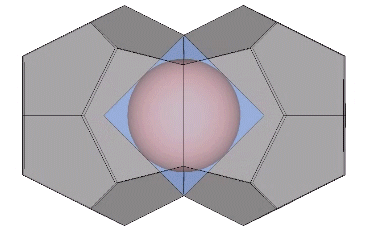
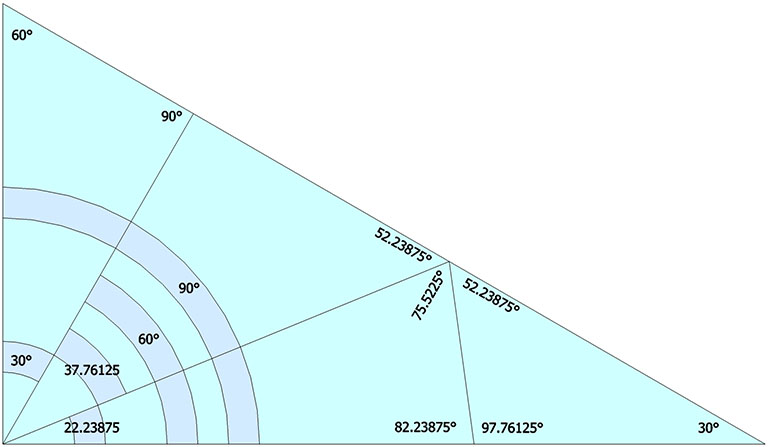
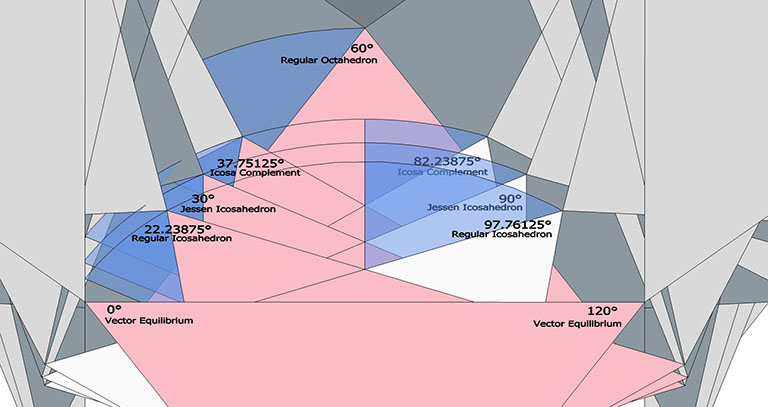
The following illustration shows how the dihedral angles of the regular icosahedron relate to the golden ratio.

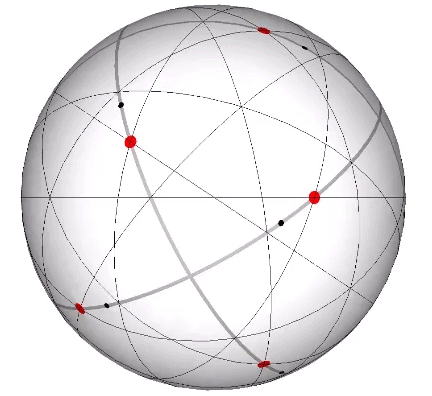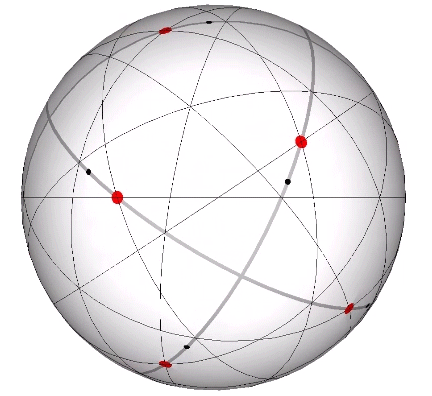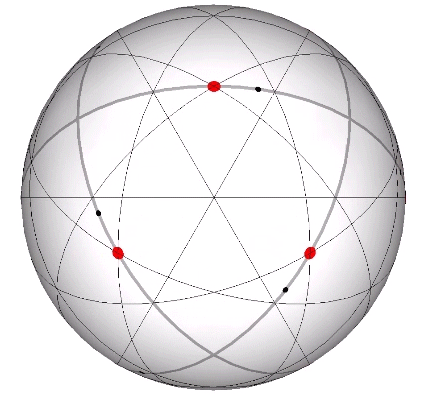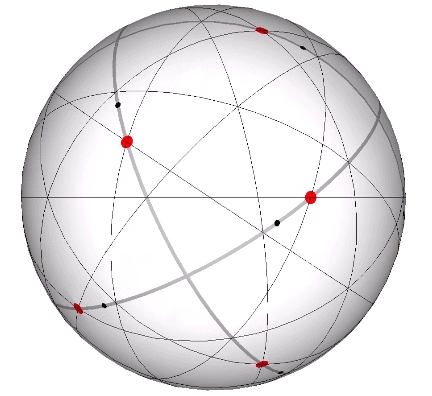
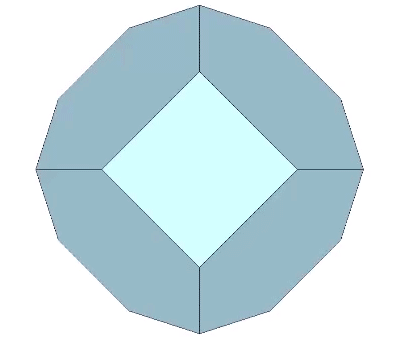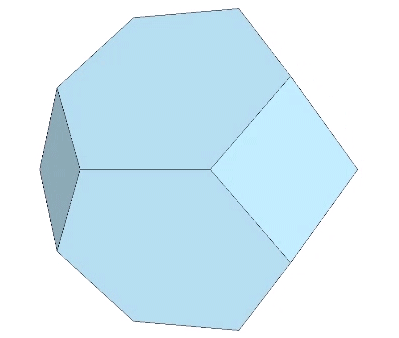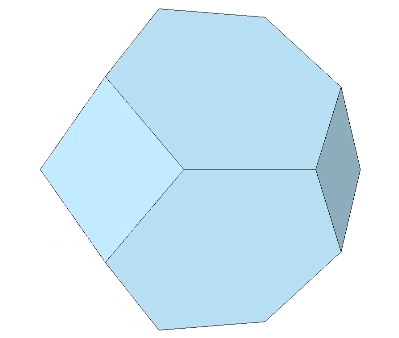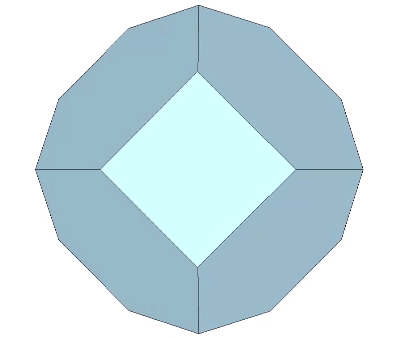
The icosahedron’s circumsphere and mid-sphere radii are the cosines of 18°, (√φ+2)/2, and 36°, φ/2, or the sines of 72° and 54°. The angles 72° and 36° define the golden triangle.

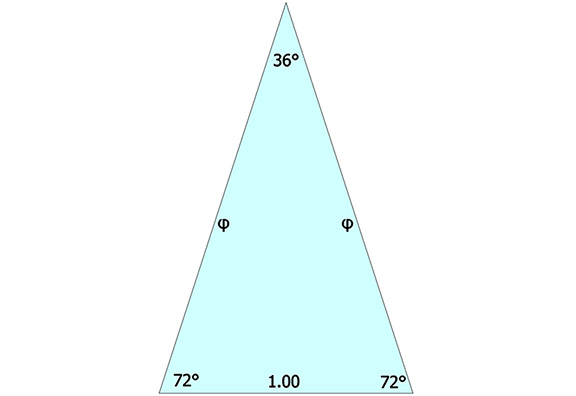
The two angles of the golden triangle are formed in the icosahedron by a lines drawn perpendicular to the circumsphere or mid-sphere radii and intersecting with a sphere of unit radius, disclosing the relationship between the icosahedron, the unit-radius sphere, and the vector equilibrium (VE).

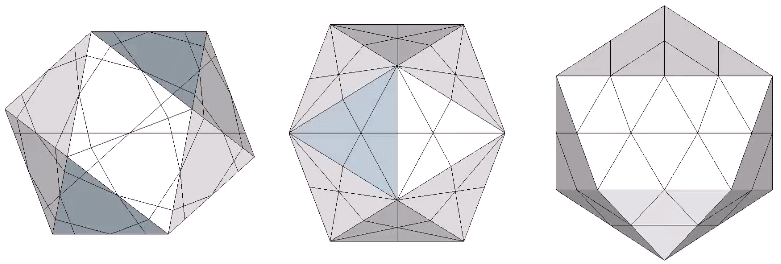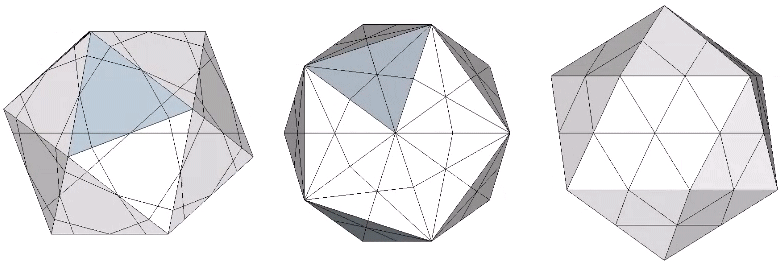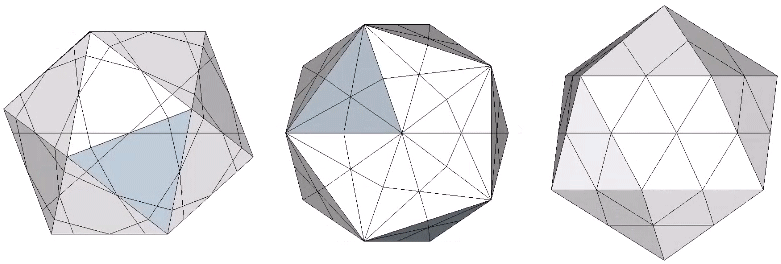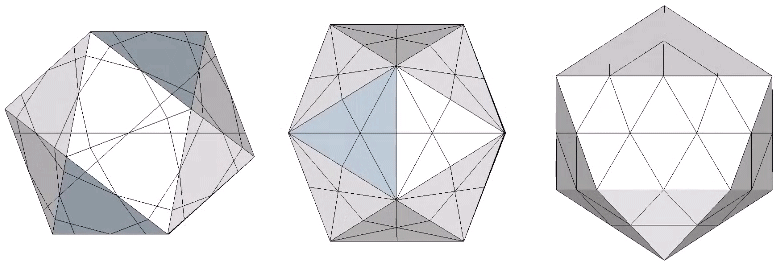
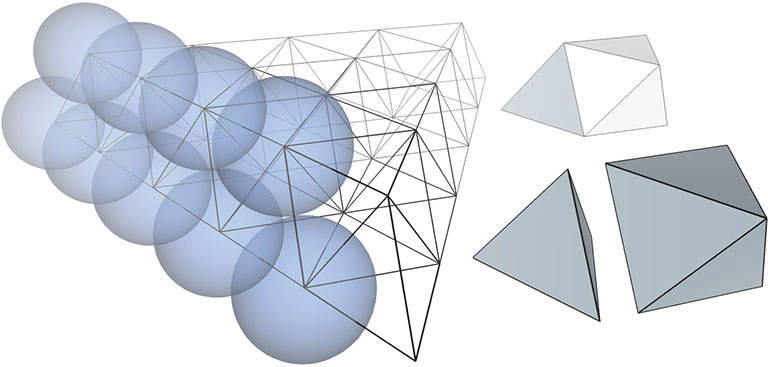
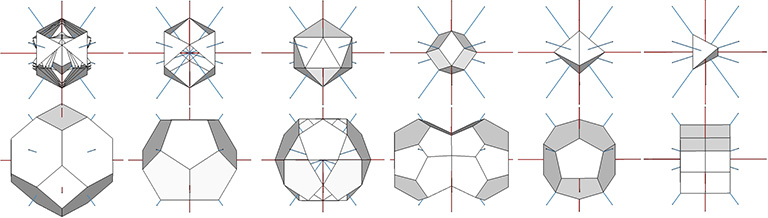
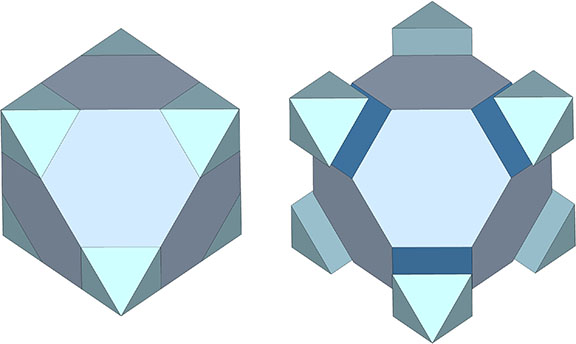
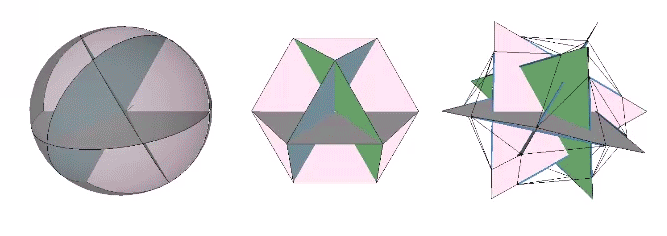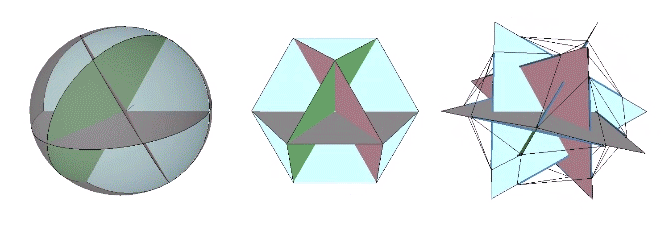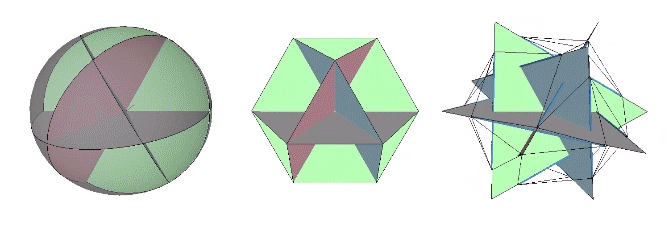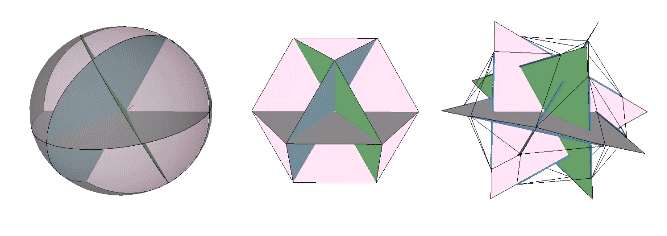
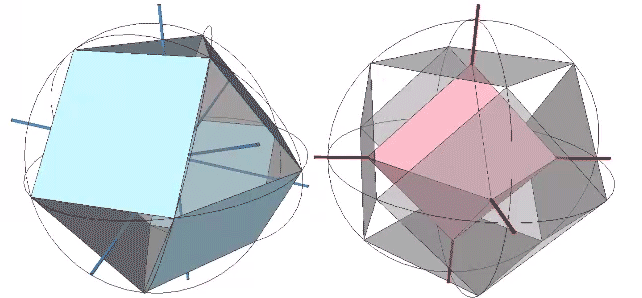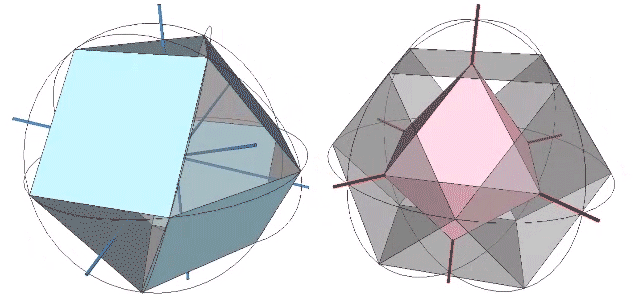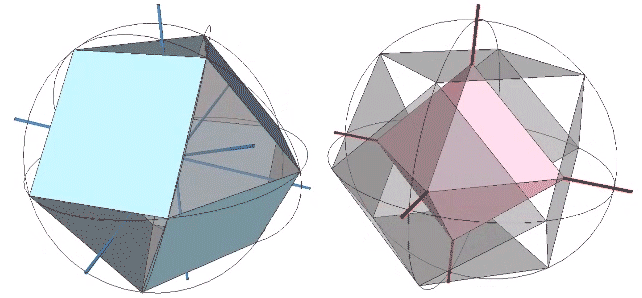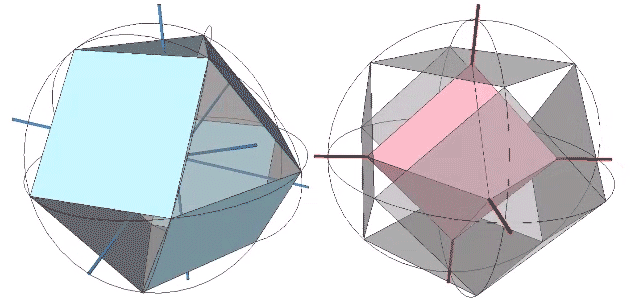
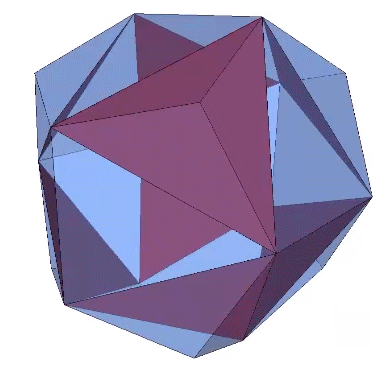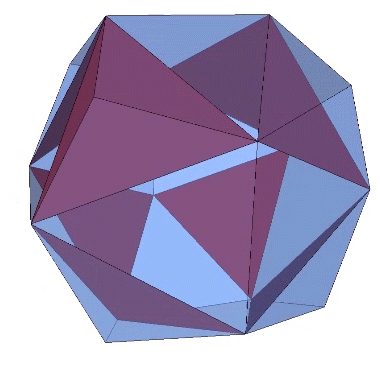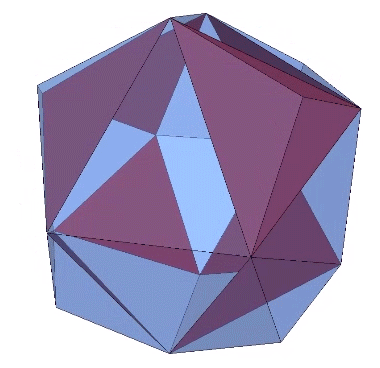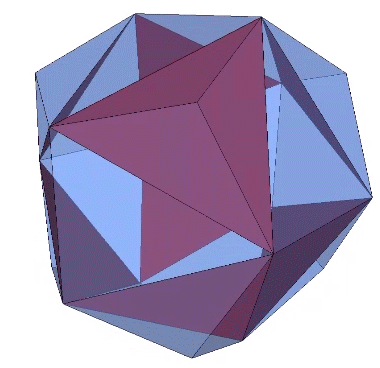
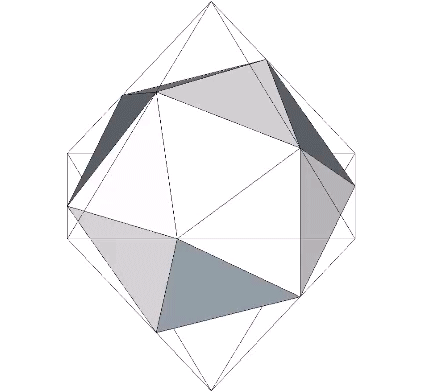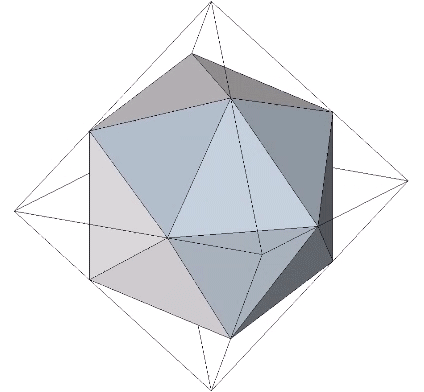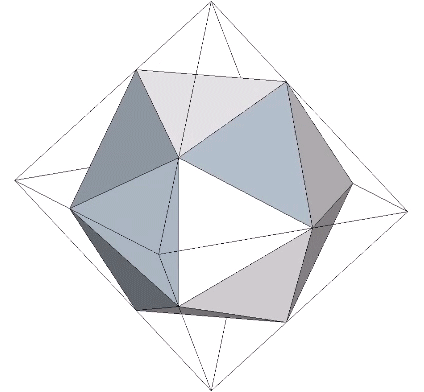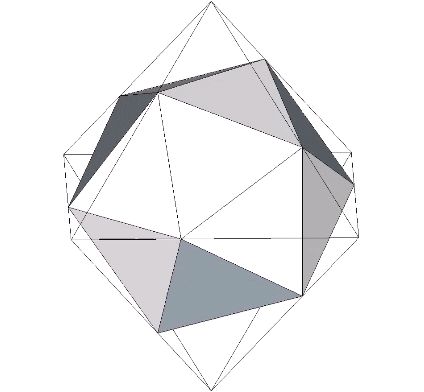
The 36° and 72° angles also show up in the face angles of the polyhedron that complements the icosahedron in the jitterbug transformation, i.e., when the VEs have contracted into the shape of the regular icosahedron, the octahedra have expanded into the shape of its complement, and vice versa. (See: Icosahedron Phases of the Jitterbug.)

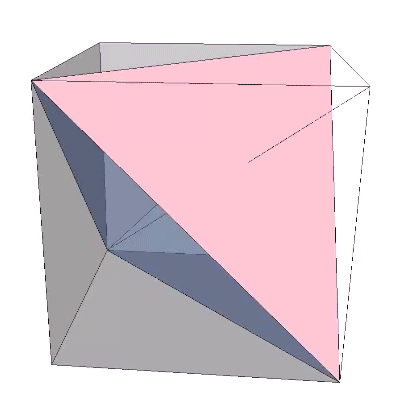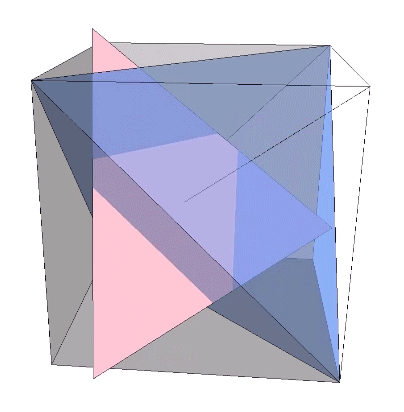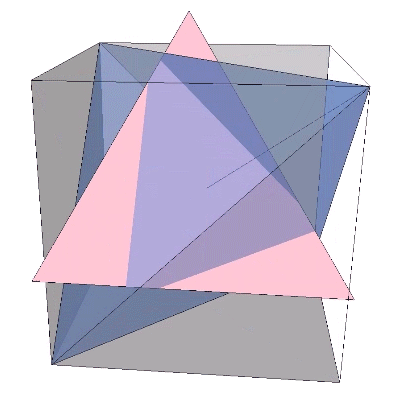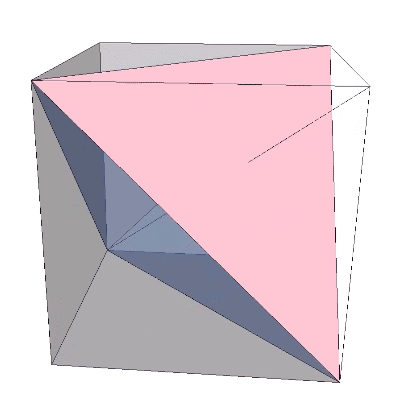
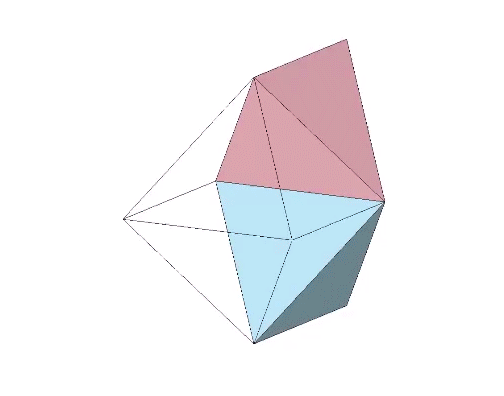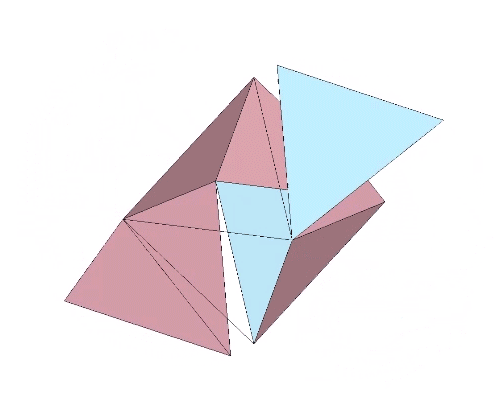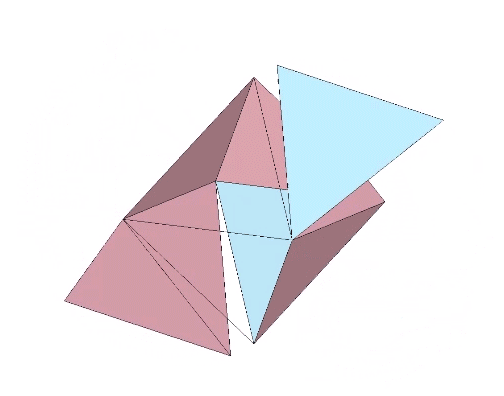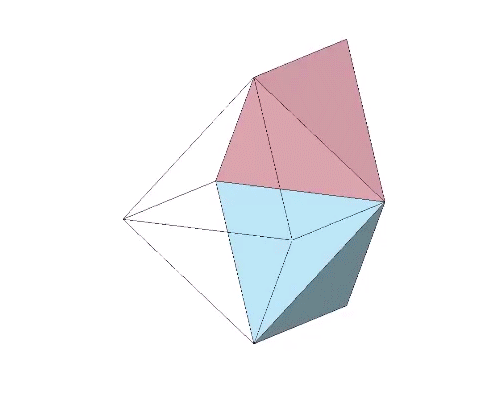
The concave forms of the regular icosahedron and its space-filling complement have, despite their different shapes, identical face angles: eight equilateral triangles (60°, 60°, 60°) and twelve isosceles triangles of 36°, 36°, 54°.

We can close up the cavities to create six irregular tetrahedra arranged orthogonally around their common centers. Curiously, the tetrahedral cavities of both the regular icosahedron and its complement have identical, rational cubic volumes of a³/12, or a combined cubic volume of a³/2, where a is the edge length.

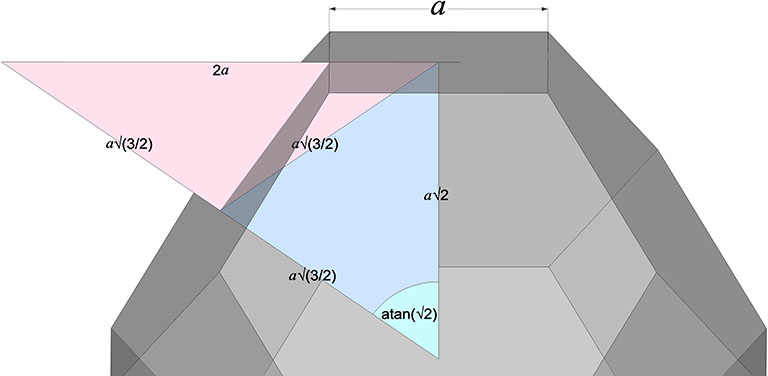
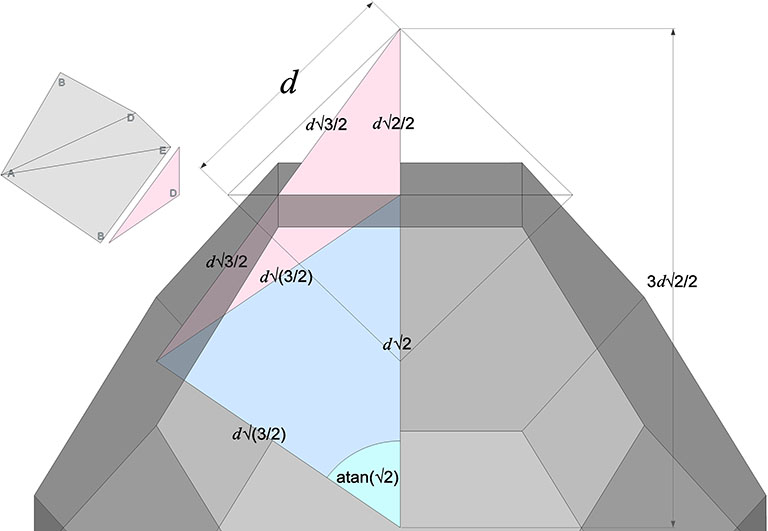
The in-sphere radius makes an angle with the mid-sphere radius of atan(2-φ), or about 20.905157°. Some tedious trigonometry works out its length to be φ²√3/6 or about 0.75576131.

The central angle, i.e. the angle between two adjacent vertices of the icosahedron and its center of volume, is the same as the angle from a square’s mid-edge to one of its opposite corners, atan(2), about 63.43894882°.

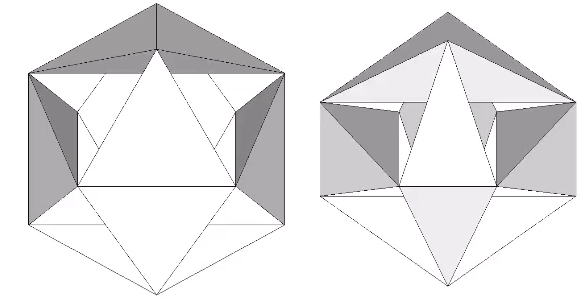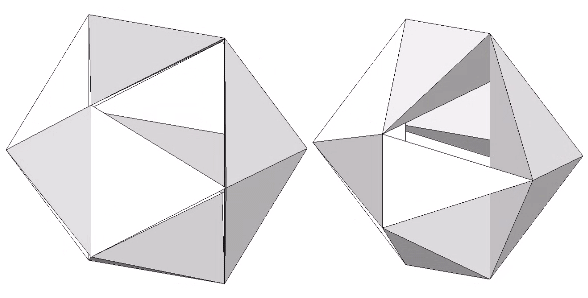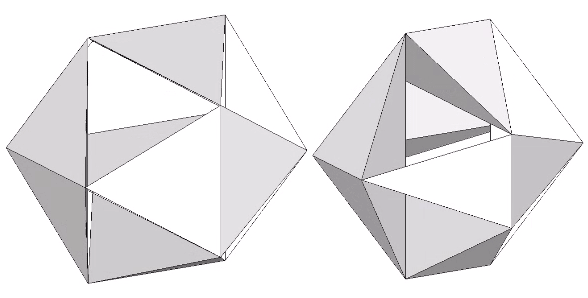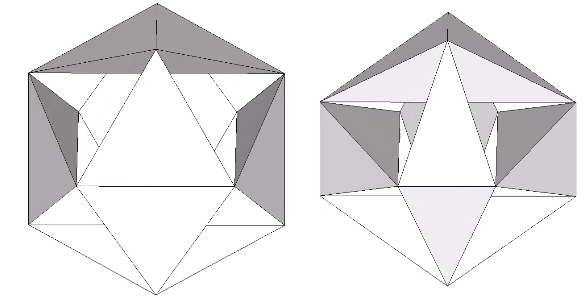
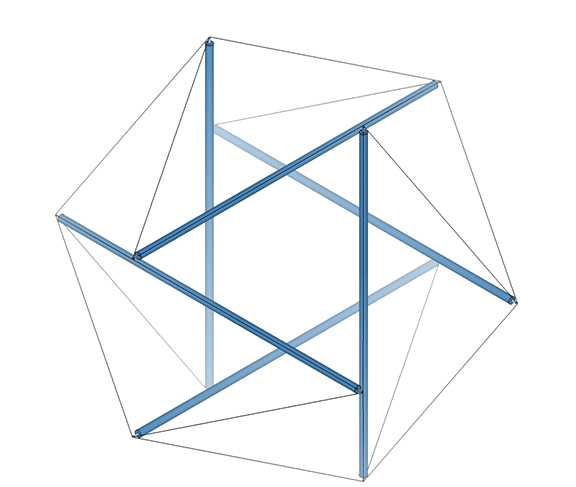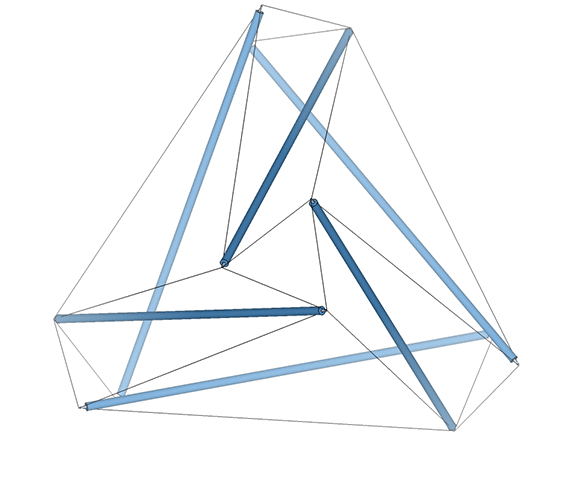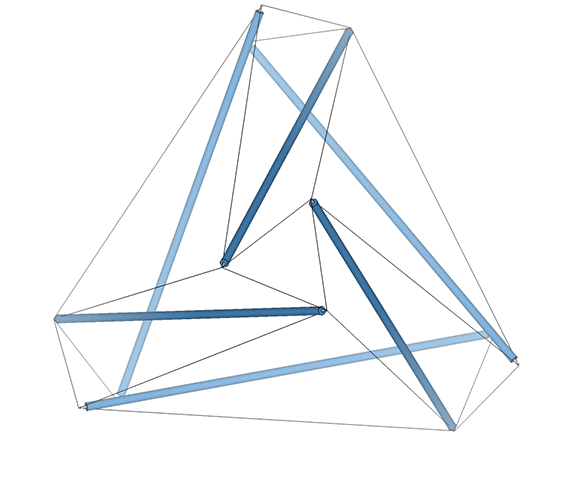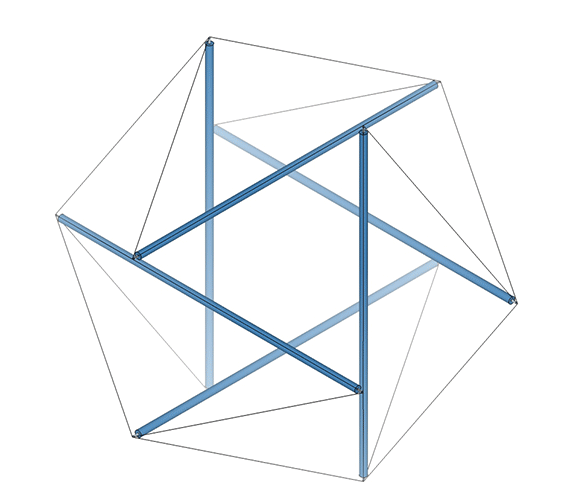
Fuller sometimes referred to the six-strut tensegrity sphere as the “tensegrity icosahedron.” Mathematicians are now calling it the Jessen Orthogonal icosahedron. See: Jessen Orthogonal Icosahedron and Tensor Equilibrium, and The Jessen Orthogonal Icosahedron in the Isotropic Vector Matrix. It would be perhaps more accurate to say that it approximates the shape of an octahedron (eight triangles, with six vertices meeting at mid-strut). But I prefer to call it “the tetrahedron in its tensor equilibrium phase.” It is also the shape that the VE and octahedron describe precisely midway through the jitterbug transformation of the isotropic vector matrix. See: Tensegrity; Tensegrity Equilibrium and Vector Equilibrium; Jitterbug, and; Icosahedron Phases of the Jitterbug.

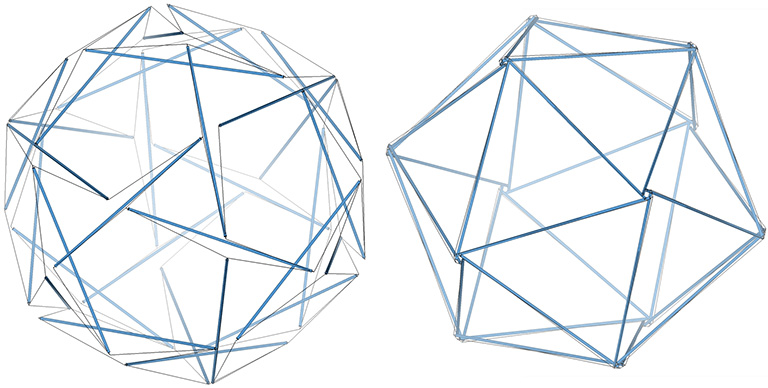
The regular icosahedron in its tensor equilibrium phase (left in the figure below) approximates the shape of the icosidodecahedron.

The icosahedron has an irrational volume and so is incommensurate with the A and B quanta modules.

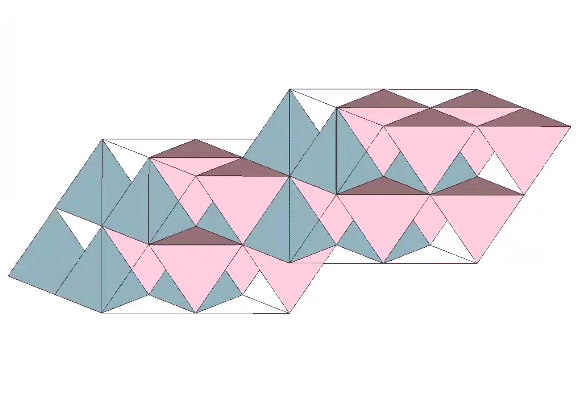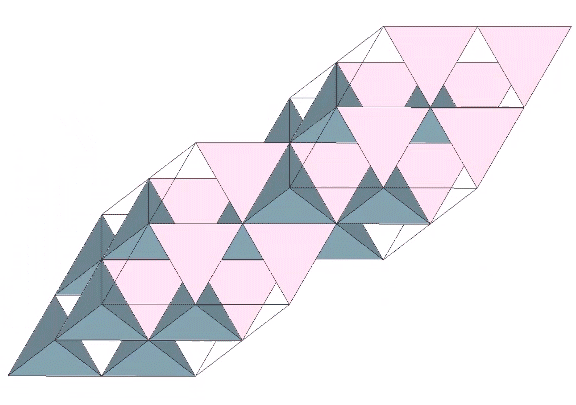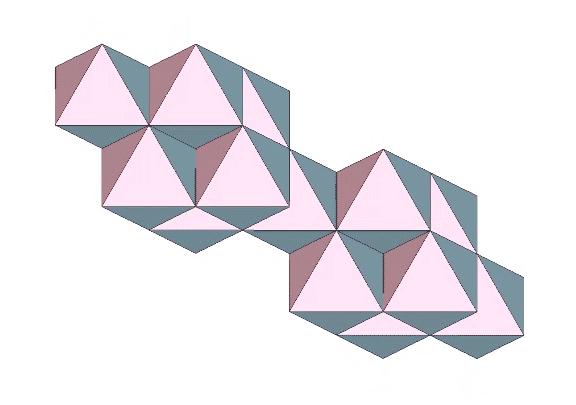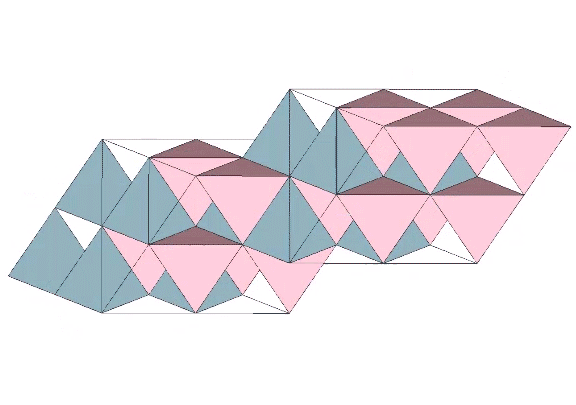
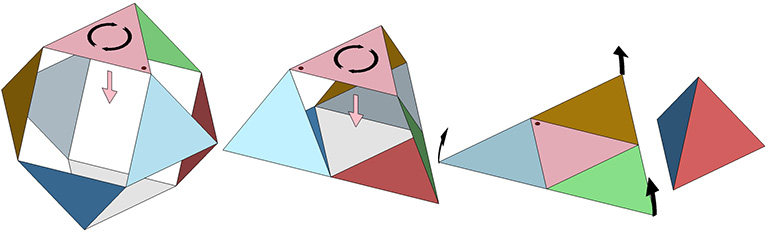
The regular icosahedron can be constructed from a single paper strip of twenty equilateral triangles.

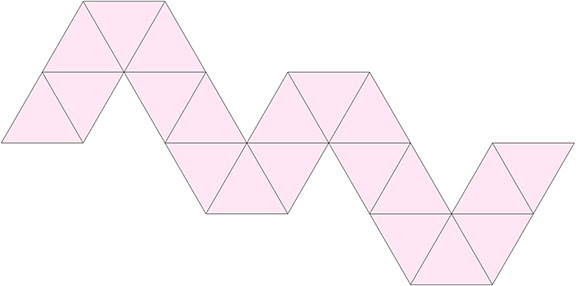
The construction is accomplished by 19 sequential folds of atan(2√5/5).

The Raleigh Edition of the Dymaxion Airocean World Map (copyright 1954) is a variation of the cartographic projection method Fuller patented in 1946. Earth’s surface is mapped onto the planar facets of the regular icosahedron by a method Fuller called “triangular geodesics transformational projection.” It is one of the most distortion-free maps of the earth’s surface every devised. Great circles approximate straight lines, and its modules can be rearranged to reveal relationships and orientations not otherwise apparent on more conventional maps.

The map folds neatly into a regular icosahedron.

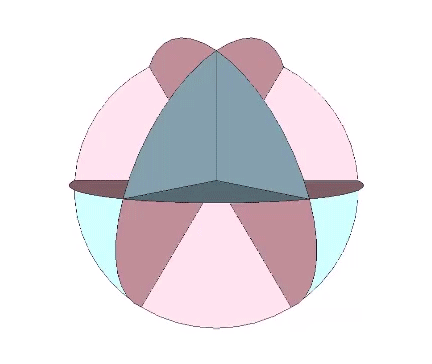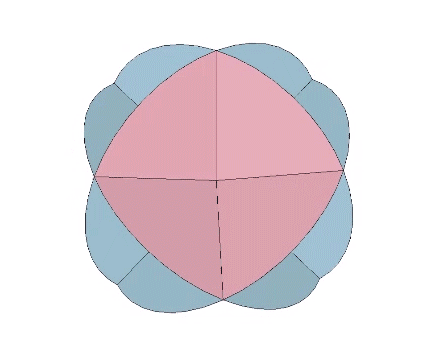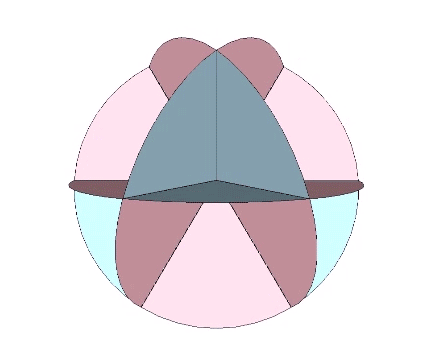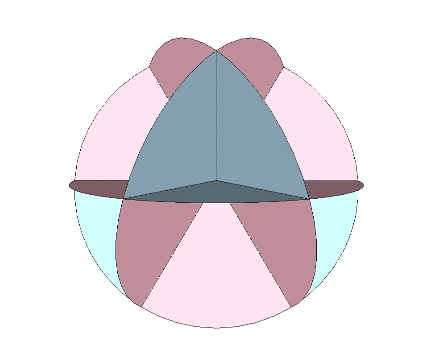
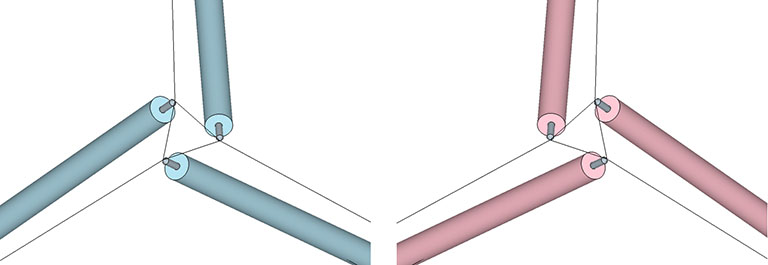
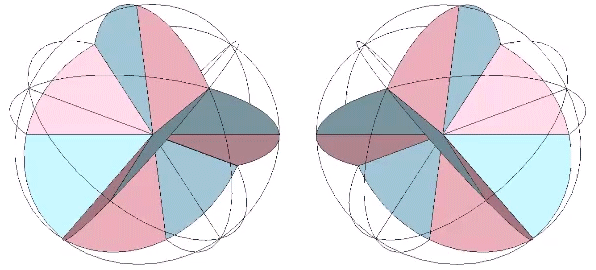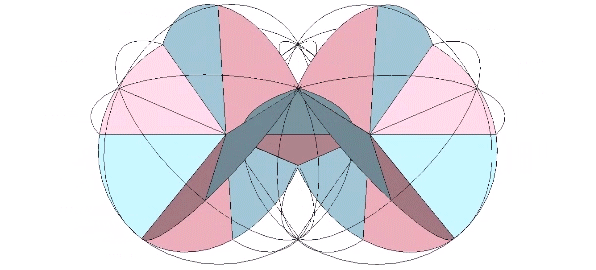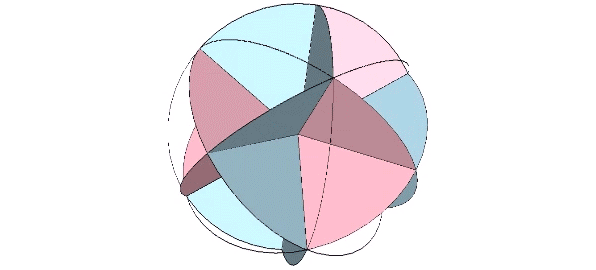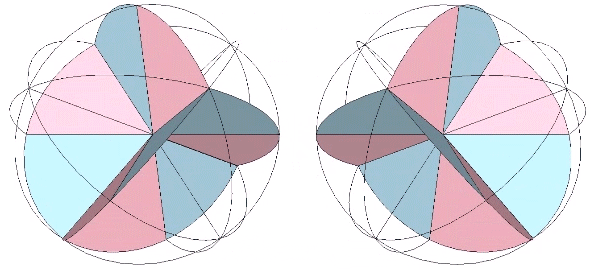
All the structural (i.e. triangulated) polyhedra may be constructed from an even number triangular helices, or what Fuller called one half of a structural quantum. The tetrahedron and icosahedron (but not the octahedron) require an equal number of clockwise and counter-clockwise helices.

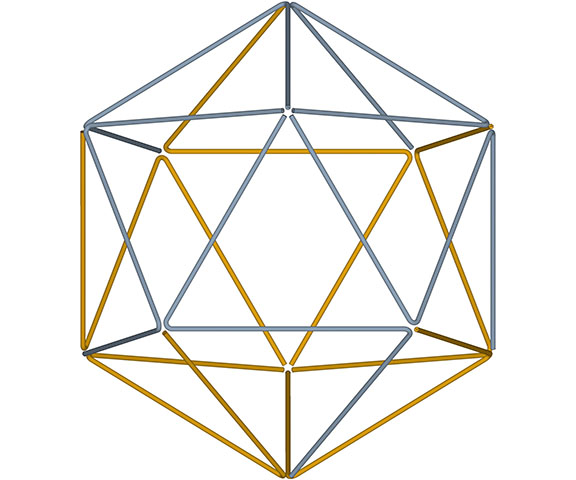
The two helices each occupy their own hemisphere, with exclusively clockwise helices in one hemisphere, and exclusively counter-clockwise helices in the other. Each radiate from diametrically opposed vertices, in effect polarizing the icosahedron on one preferred axis of spin. See also: Isotropic Vector Matrix as Transverse Waves.)

See also: The 31 Great Circles of the Icosahedron (new illustrations).

“The 31 great circles of the icosahedron always shunt the energies into local-holding great-circle orbits, while the vector equilibrium opens the switching to omni-universe energy travel. The icosahedron is red light, holding, no-go; whereas vector equilibrium is green light, go. The six great circles of the icosahedron act as holding patterns for energies. The 25 great circles of the vector equilibrium all go through the 12 tangential contact points bridging between the 12 atomic spheres always closest packed around any one spherical atom domain.”
— R. Buckminster Fuller, Synergetics, 1132.02

“The six great circles of the icosahedron are the only ones not to go through the potential inter-tangency points of the closest-packed unit radius spheres, ergo energy shunted onto the six icosahedron great circles becomes locked into local holding patterns, which is not dissimilar to the electron charge behaviors.”
— ibid. 457.22

In Fuller’s energetic geometry, the great circles of the VE and icosahedron model energy transference and containment. He described them as “railroad tracks” which either move energy from one domain to another, or divert energy into into loops or holding patterns. Communication occurs when a great circle of one sphere crosses a great circle of an adjacent sphere, i.e. crosses a point of contact or, in Fuller’s terminology, a “kissing point.” All of the 25 great circles of the VE intersect at least two points of contact with neighboring spheres. This is consistent with the role of the VE in the isotropic vector matrix and what Fuller called “nature’s coordinate system.” Of the 31 great circles of the icosahedron, only 7 intersect with the isotropic vector matrix, and these are identical with the sets of 3 and 4 great circles of the VE and the seven axes of symmetry. This isolation is consistent with Fuller’s conception of the icosahedron as a model of potential energy or charge. Of the remaining 24 great circles of the icosahedron, 18 interse ct with adjacent spheres only when close-packed as icosahedral shells, and 6 are true holding patterns, communicating with neither the isotropic vector matrix of radially close-packed spheres, nor with the icosahedron shells of laterally close-packed spheres. (See: Close-Packing of Spheres)

The 10 face-to-face axes, the 15 edge-to-edge axes, and the 6 vertex-to-vertex axes define the 31 great circles of the icosahedron.

The 31 great circles of the icosahedron disclose the following spherical polyhedra: octahedron; icosahedron; pentagonal dodecahedon; icosidodecahedron; tricontahedron; and VE. See Icosahedron: Spherical Polyhedra Disclosed by Great Circles.

Only seven of the 31 great circles of the icosahedron pass through points of contact between the radially close-packed spheres of the isotropic vector matrix. Their axes are the identical with Fuller’s Seven Axes of Symmetry. These include 4 of the 10 great circles defined by the ten face-to-face axes of the icosahedron (these are the same 4 associated with the VE’s triangular face-to-face axes), and 3 of the 15 great circles defined by the fifteen edge-to-edge axes of the icosahedron (these are the same 3 associated with the VE’s square face-to-face axes). (See: The 25 Great Circles of the Vector Equilibrium.) All of the great circles which are unique to the icosahedron pass through none of the points of contact between the radially close-packed spheres, and are therefore what Fuller called “local-holding great-circle orbits.”

The 15 great circles of the icosahedron each pass through four of the twelve vertices of the icosahedron, and therefore provide communication between spheres close-packed as discrete icosahedron shells or lattices (See: Close Packing of Spheres, and Close Packing of Icosahedra. The 6 great circles of the icosahedron pass through neither the vertices of VE nor those of the icosahedron, and are therefore true holding patterns, providing no inter-sphere communication.

In the figures below, the referenced great circles are indicated by the thin black lines, the points of contact between radially close-packed spheres of the isotropic matrix, or the vertices of the VE, are indicated by red dots. The points of contact between spheres close-packed into discrete icosahedral shells or lattices, or vertices of the icosahedron, are indicted by black dots. The paths followed by the vertices in the jitterbug transformation are indicated by thick gray lines.

Set of 15 (Axes Connect Opposing Edges)

The 15 great circles defined by the set of fifteen edge-to-edge axes of the icosahedron disclose the spherical pentagonal dodecahedron and the Basic Disequilibrium LCD Triangle. Each of the fifteen great circles passes through four of the twelve vertices of the icosahedron, and each vertex of the icosahedron connects with five great circles. Three of the fifteen pass through the vertices of the VE, and these are identical with the VE’s 3 great circles defined by its three square face-to-face axes of spin.

Set of 10 (Axes Connect Opposing Faces)

The 10 great circles defined by the set of ten face-to-face axes of the icosahedron disclose the spherical vector equilibrium (VE). None pass through the vertices of the icosahedron. Four pass through the vertices of the VE, and these are identical with the VE’s 4 great circles which describe the spherical VE.

Set of 6 (Axes Connect Opposing Vertices)

The 6 great circles defined by the set of six vertex-to-vertex axes of the icosahedron disclose the spherical icosidodecaheron, the 42-sided polyhedron associated with the spherical form of the 30-strut tensegrity icosahedron. (See: Tensegrity.) None pass through a vertex, neither of the VE nor of the icosahedron, and therefore provide no inter-sphere communication.

For discussion on the surface and central angles described by the 31 great circles of the icosahedron, see Basic Disequilibrium LCD Triangle.

See also: The 25 Great Circles of the VE (new illustrations).

“The vector equilibrium’s 25 great circles, all of which pass through the 12 vertexes, represent the only most economical lines of energy travel from one sphere to another. The 25 great circles constitute all the possible most economical railroad tracks of energy travel from one atom to another of the same chemical elements. Energy can and does travel from sphere to sphere of closest-packed sphere agglomerations only by following the 25 surface great circles of the vector equilibrium, always accomplishing the most economical travel distances through the only 12 points of closest-packed tangency.”
— R. Buckminster Fuller, Synergetics, 452.02

In Fuller’s energetic geometry, the great circles of the VE and icosahedron model energy transference and containment. He described them as “railroad tracks” which either move energy from one domain to another, or divert energy into into loops or holding patterns. Communication occurs when a great circle of one sphere crosses a great circle of an adjacent sphere, i.e. crosses a point of contact or, in Fuller’s terminology, a “kissing point.” All of the 25 great circles of the VE intersect at least two points of contact with neighboring spheres. This is consistent with the role of the VE in the isotropic vector matrix and what Fuller called “nature’s coordinate system.” Of the 31 great circles of the icosahedron, only 7 intersect with the isotropic vector matrix, and these are identical with the sets of 3 and 4 great circles of the VE and the seven axes of symmetry. This isolation is consistent with Fuller’s conception of the icosahedron as a model of potential energy or charge. Of the remaining 24 great circles of the icosahedron, 18 intersect with adjacent spheres only when close-packed as icosahedral shells, and 6 are true holding patterns, communicating with neither the isotropic vector matrix of radially close-packed spheres, nor with the icosahedron shells of laterally close-packed spheres. (See: Close-Packing of Spheres)

The 25 great circles of the vector equilibrium (VE) are derived from its 25 axes of spin: 12 edge-to-edge axes; 6 vertex-to-vertex axes, 4 triangular-face-to-triangular-face axes; and 3 square-face-to-square-face axes.

The 25 great circles disclose the following polyhedra: the octahedon; the vector equilibrium (VE); the tetrahedron; the rhombic dodecahedron; and the cube. See VE: Spherical Polyhedra Disclosed by Great Circles. The sets of 6 and 3 great circles divide the sphere’s surface into the 48 Basic Equilibrium LCD Triangles.

All 25 great circles of the VE pass through one or more points of contact between the radially close-packed spheres of the isotropic vector matrix. In the figures below, the referenced great circles are indicated by the thin black lines, the points of contact, or the vertices of the VE, are indicated by red dots. The vertices of the regular icosahedron are indicated by black dots, and the paths the vertices follow in the jitterbug transformation are indicated by gray lines.

Set of 12 (Axes Connect Opposite Edges of VE)

The set of 12 great circles of the VE create a spider web pattern that appears more random than the other great circle sets. In combination with the sets 6 and 4 great circles, the 12 great circles describe an alternate octahedron, but otherwise disclose no other recognizable patterns. Combined, the 12 great circles pass through all 12 points of tangency with neighboring spheres in the isotropic vector matrix.

Set of 6 (Axes Connect Opposite Vertices of VE)

The set of 6 great circles of the VE describe the spherical rhombic dodecahedron, cube, and tetrahedron. Combined, the 6 great circles pass through all 12 points of tangency with neighboring spheres in the isotropic vector matrix.

Set of 4 (Axes Connect Opposing Triangular Faces of VE)

The set of 4 great circles of the VE describe the spherical vector equilibrium. Each intersects with 6 points of tangency with neighboring spheres in the isotropic vector matrix, and the set as a whole passes through all 12 points of tangency. The set of 4 great circles in combination with the set of 3 great circles of the VE comprise the seven axes of symmetry.

Set of 3 (Axes Connect Opposing Square Faces of VE)

The set of 3 great circles of the VE describe the spherical octahedron. Each intersects with 4 points of tangency with the isotropic vector matrix, and the set as a whole intersects with all 12 points of tangency. The set of the 3 great circles in combination with the set of 4 great circles of the VE comprise the seven axes of symmetry.

For a discussion of the surface and central angles formed by the 25 great circles of the VE, see, The Basic Equilibrium LCD Triangle.

“When the centers of equiradius spheres in closest packing are joined by most economical lines, i.e., by geodesic vectorial lines, an isotropic vector matrix is disclosed, ‘isotropic’ meaning “everywhere the same,” ‘isotropic vector’ meaning “everywhere the same energy conditions.” This matrix constitutes an array of equilateral triangles that corresponds with the comprehensive coordination of nature’s most economical, most comfortable, structural interrelationships employing 60-degree association and disassociation. Remove the spheres and leave the vectors, and you have the octahedron-tetrahedron complex, the octet truss, the isotropic vector matrix.”
— R. Buckminster Fuller, Synergetics, 420.01

“Euclid was not trying to express forces. We, however … are exploring the possible establishment of an operationally strict vectorial geometry field, which is an isotropic (everywhere the same) vector matrix. We abandon the Greek perpendicularity of construction and find ourselves operationally in an omnidirectional, spherically observed, multidimensional, omni-intertransforming Universe.”
— ibid. 825.28

The vector equilibrium (VE) and the isotropic vector matrix constitute the core of Fuller’s geometry. Its discovery is one of Fuller’s earliest memories, from a kindergarten class in his childhood home of Milton, Massachusetts. Given semi-dried peas and toothpicks, and a visual deficit as yet uncorrected by the strong glasses he wore all his life, he fumbled sightlessly, and through touch alone constructed what he would later name the octet truss. His classmates constructed cubes and the gabled house-like shapes they were familiar with. Fuller constructed something that satisfied his sense of touch rather than his sense of sight, a sense which could easily have been prejudiced by the cubes and right angles of his built environment. Instead, his fingers naturally sought out and found the triangle, the tetrahedron, and the octahedron, arrangements which, unlike squares and cubes, held their shape and could not be deformed. He credits his kindergarten teacher, Miss Parker of Milton, Massachusetts, with the discovery; it was her praise and kind remarks that fixed the experience in his memory and, eventually, would inspire a lifelong critique of conventional geometry, and his explorations into the energetic-synergetic geometry of nature.

The isotropic vector matrix is the geometric analog to Fuller’s more general statement of Avogadro’s proposition, that “under identical, unconstrained, and freely self-interarranging conditions of energy all elements will disclose the same number of fundamental somethings per given volume.” Fuller’s geometry replaces the abstract concept of infinite lines and line segments with the physical concept of energy vectors. A geometric model of Avogadro’s equilibrium state must have all energy vectors of equal length, i.e. equal products of mass times velocity, and all interacting at the same angles. All vectors in the isotropic vector matrix therefore are of equal length, i.e. the diameter (or two times the radius) of the uniform sphere, and all interact with the others at exactly 60°.

Construction can be accomplished by vertex-bonded (positive or negative) tetrahedra, or by edge-bonded octahedra. Positive-tetrahedron or negative-tetrahedron constructions (but not both) produce a matrix of single vectors, while the octahedron constructions produce a matrix of doubled vectors. Edge-bonding positive and negative tetrahedron together produces a doubled-vector matrix complementary to the doubled-vector octahedron construction.

Each of the two constructions (edge-bonded positive and negative tetrahedra, and edge-bonded octahedra) can be transformed into the other by turning themselves inside out. Note that this inside-out transformation results in the same matrix, one emphasizing the tetrahedra and the other emphasizing the octahedra; there is no shifting of vertices or exchanging of spheres and spaces as in The Jitterbug transformations.

All of the models of the isotropic vector matrix can be broken down into the following:

1. spheres,
2. spaces, and;
3. interstices.

In the vector model, the sphere is represented by the vector equilibrium (VE), the space by the octahedron, and the interstices by positive and negative tetrahedra. In the quanta model, spaces and spheres are represented by the two constructions of rhombic dodecahedron, and the interstices appear as tetrahedra or cubes. In the spheres and interstitial models, the spheres are represented, obviously, by spheres, the spaces are represented by concave VEs inside of the octahedra, and the interstices are represented as concave octahedra inside of the tetrahedra.

See also: Spheres and Spaces; A and B Quanta Modules; and Quanta Module Constructions of the Rhombic Dodecahedron.

Fuller has two definitions for his “seven axes of symmetry.” The first definition relates to the great circle sets of the vector equilibrium (VE) and the icosahedron. The 25 great circles of the VE are defined by four sets of axes, and the 31 great circles of the icosahedron are defined by three sets of axes. 4+3=7.

The second definition applies to a subset of the first. Fuller noted that truncations through the vertices and edges of the regular tetrahedron produces a tetrakaidecahedron with six square and eight hexagonal faces. (Truncating the faces will produce only a smaller tetrahedron.) The tetrakaidecahedron has fourteen faces, lines through the centers of which define seven axes of spin. Coordinated truncations produce the Kelvin truncated octahedron, which is associated with nuclear domains in the isotropic vector matrix, and with the optimal cellular packing of the Weaire-Phelan matrix (see Tetrakaidecahedron and Pyritohedron).

The Seven Axes of Symmetry are identical with the seven face-to-face axes of the VE, and correspond to four of the icosahedron’s ten face-to-face axes and three of its fifteen edge-to-edge axes. The great circles defined by the set of 4 axes discloses the spherical VE (red in the figure below), and the great circles defined by the set of 3 axes defines the spherical octahedron (blue in the figure below).

All the regular polyhedra, as well as other polyhedra significant to Fuller’s geometry, align with the Seven Axes of Symmetry.

“The tetrakaidecahedron (Lord Kelvin’s “Solid”) is the most nearly spherical of the regular conventional polyhedra; ergo, it provides the most volume for the least surface and the most unobstructed surface for the rollability of least effort into the shallowest nests of closest-packed, most securely self-cohering, allspace- filling, symmetrical, nuclear system agglomerations with the minimum complexity of inherently concentric shell layers around a nuclear center.“
—R. Buckminster Fuller, Synergetics, 942.70

The Kelvin truncated octahedron, or Kelvin, is a space-filling, fourteen-sided polyhedron with eight hexagonal faces and six square faces, all of equal edge-length. It got its name from a problem posed by Lord Kelvin in the 19th century, to find an arrangement of cells of equal volume so that their total surface area is minimized.

Note: Fuller refers to this shape as the tetrakaidecahedron, a generic term for all 14-sided polyhedra. I reserve this term for the all-space filling complement to the pyritohedron in the Weire-Phelan matrix. See Tetrakaidecahedron and Pyritohedron.

Angles and dimensions of the Kelvin tetrakaidecahedron or truncated octahedron with edge length a:

• 14 faces (8 hexagonal and 6 square), 24 vertices, 36 edges
• Face angles: 90°, 120°, 120°
• Dihedral angle: arccos(-√3/3) ≈ 125.264390°
• Central angle of edge: atan(3/4) ≈ 36.869898°
• Volume (in tetrahedra): 96a³
• Volume (in cubes): 11a³√2
• A quanta modules: 1,536
• B quanta modules: 768
• Surface area (in equilateral triangles): 8a²(6+√3)
• Surface area (in squares): 6a²(1+2√3)
• In-sphere radius (center to mid-hexagonal-face): a√(3/2) = a√6/2
• In-sphere radius (center to mid-square face): a√2
• Mid-sphere radius (center to mid-edge): 3a/2
• Circumsphere radius (center to vertex): a√(5/2)

Fuller noted that the Kelvin defined nuclear domains in the radial close-packing of unit-radius spheres.

Presently the best solution to the Kelvin problem is the Weaire-Phalen matrix, consisting of pyritohedra and tetrakaidecahedra. Perhaps not surprisingly, the Kelvin can be derived from from this matrix. Connecting radials of the tetrakaidecahedra forms the very same Kelvin as above. Its edges are of unit-length, the same as the spheres’ diameters.

It may be easier to see how the Kelvin faces are derived from the radials of the tetrakaidecahedron if we examine one of its square faces and one of its hexagonal faces individually. The pink spheres in the illustrations below are the non-unique nuclei, those nuclei whose shells are shared with their neighbors. See Formation and Distribution of Nuclei in Radial Close-Packing of Spheres.

The two in-sphere radii—from center to mid-square-face, and from center mid-hexagonal-face—make an angle of arctan(√2) ≈ 54.735610° with each other. A line drawn between the mid-faces creates an isosceles triangle with a base of a√2 and sides of a√(3/2). Extending the mid-hexagon-face radius to where it crosses a line drawn perpendicular from the mid-square-face radius creates an isosceles triangle with a base of 2a (where a = edge length, unity, or sphere diameter) and sides of a√(3/2). Combining the two isosceles triangles creates a right triangle whose legs measure a√2 and 2a, and whose hypotenuse measures 2×a√(3/2) = a√6.

This triangle maps to the distribution of nuclei in the isotropic vector matrix, with unique nuclei centered on the vertices of the two non-right angles, and the nuclei that share their shells with adjacent nuclei centered on the right angle’s vertex.

Note that in the illustrations below, d = a = the sphere diameter. Unique nuclei are colored red, non-unique nuclei are pink, and the spheres occupying the shells of nuclei are white.

Extending the mid-square-face radius to a point where it crosses a line drawn perpendicular to the mid-hexagon-face radius creates a scalene triangle whose angles are curiously identical with the interior face of the B quanta module. Combining this scalene triangle with the isosceles triangle mentioned above creates a right triangle whose legs measure 2d√2/2 and d√(3/2). The mid-square-face radius extends d√2/2 beyond the face, exactly half of the face’s diagonal length, and half the mid-square-face radius. This suggests a rotational transformation of the Kelvin that may shadow the space-to-sphere, sphere-to-space transformations of the isotropic vector matrix, something begging to be investigated further, along with that curious appearance of the interior face of the B quanta module (pink in the illustration below).

If we replace the twelve vertices of a one-frequency Kelvin with spheres, we find that they occupy the spaces between the 42 spheres of the two 2-frequency vector equilibrium (VE) shell. The 2-frequency VE is significant because its shell is the last to fully enclose the nucleus without containing any new potential nuclei. The 1-frequency Kelvin complements the 2-frequency VE to fully isolate unique nuclear domains.

Kelvins with even frequencies (odd numbers of spheres to the side) are coincident with the radially close-packed spheres of the isotropic vector matrix. Those with odd frequencies (even numbers of spheres to the side) occupy the spaces between radially close-packed spheres.

At the center of odd Kelvins is a space, i.e., concave VE, and at the center of even Kelvins is a sphere. Note that the odd Kelvins in the above examples which fully isolate the nucleus have been shifted by 1/2 of a sphere diameter out of their natural position in the matrix. (See also: Spaces and Spheres (Redux), and; Spheres and Spaces.)

In the figures below, spheres and spaces are represented by the two quanta module constructions of the rhombic dodecahedron.

Fuller conceived the Kelvin as a truncated tetrahedron…

…and associated it with his Seven Axes of Symmetry.

Fuller’s conception of the Kelvin as a truncated tetrahedron, rather than a truncated octahedron, is perhaps due to its association with the spherical form of the tensegrity tetrahedron, the six-strut tensegrity sphere or Jessen Orthogonal Icosahedron.

“The geometrical model of energy configurations in synergetics is developed from a symmetrical cluster of spheres, in which each sphere is a model of a field of energy all of whose forces tend to coordinate themselves, shuntingly or pulsatively, and only momentarily in positive or negative asymmetrical patterns relative to, but never congruent with, the eternality of the vector equilibrium. “
— R. Buckminster Fuller, Synergetics, section 205.01

Vectors connecting the centers of unit-radius spheres clustered around a common nucleus define the VE, or vector equilibrium.

In the VE, the number of modular subdivisions, i.e. frequency, of the radii is exactly the same as the number of modular subdivisions of the chords. Frequency may refer, then, to the number of shells surrounding the nucleus or to the number of subdivisions of any edge vector.

The radial close packing of equal radius spheres about a nuclear sphere forms vector equilibria of progressively higher frequencies. The number of spheres in the outer shell is always the frequency (F)—the number of subdivisions of the radial or edge vectors running through the sphere centers—raised to the second power, which is then multiplied by ten, then added to two, or 10F²+2. In the illustration below, the F1 VE (with unit radial and edge vectors) has twelve spheres in its outer shell: (10×1)+2=12. The F2 VE (whose radial and edge vectors have been divided into two subdivisions) has 42 spheres in its outer shell: (10×2²)+2=42. The F3 VE (with three subdivisions) has 92 spheres in its outer shell: (10×3²)+2=92.

Shell Volume (in spheres or vertices) of VE = 10F²+2

The cumulative number of spheres in a radially close-packed array is therefore:

10(F₁²+F₂²+F₃²+ … +F_n²)+2F_n+1,

which integrates to:

(20F³+30F²+22F+6)/6

The polyhedral shape of these nuclear assemblages of closest-packed spheres is always that of the vector equilibrium, having always six square, and eight triangular faces, for a total of fourteen. The square faces are the equatorial sections of six half-octahedra, and the triangular faces are the bases of eight tetrahedra. If the tetrahedron is taken as unity, the volume of the vector equilibrium is twenty (20). The volume in tetrahedra of any series of vector equilibria of progressively higher frequencies is always frequency to the third power times 20.

Volume (in tetrahedra) of VE = 20F³

The VE is the only construction of radially close-packed spheres that produces uniform and uninterrupted layers. Radial close-packing as octahedra is achieved only with even-numbered layers (odd numbered layers are centered on spaces), and radial close packing as tetrahedra and cubes is achieved only with every other even layer (odd numbered layers are centered on either a positive or a negative tetrahedron, and every other even layer is centered on a space).

In A and B quanta modules, the VE of frequency, F, equal to 1 consists of 336 A quanta modules and 144 B quanta modules for a total of 480 quanta, a volume of 480÷24=20 tetrahedra.

The polyhedron associated with the external shape of the VE is conventionally recognized as the cuboctahedron, or the truncated cube. That its edge lengths are identical to the length of its circumsphere radii was perhaps less well known, and its association with the radial close-packing of unit-radius spheres was either unknown or dismissed by mathematicians as of peripheral interest. For Fuller, these characteristics were central to his search for the geometric analog to his more general statement of Avogadro’s proposition, that under under identical, unconstrained, and freely self-interarranging conditions of energy all elements will disclose the same number of fundamental somethings per given volume. This was discovered to be his octet truss, or isotropic vector matrix, and the vector equilibrium (VE) is its metonymous form.

The question of structure, too, has historically been peripheral to the study of pure geometry; the subject was left to the engineers, and the engineers had for millennia been mostly stone masons for whom one geometric shape was as solid as the next. Fuller’s octet truss and geodesic structures were unknown until the “space age” of the mid-twentieth century. In the absence of its radial vectors, the remaining circumferential (edge) vectors of the cuboctahedron are left unsupported and will collapse, just as the vector model of the cube it was based on will collapse without additional triangulation. Neither is structural, if by “structure” we mean something that holds its shape without external support. In the absence of gravity and the solid earth beneath them, few man-made structures fit this definition.

A third point of contention that Fuller had with conventional geometry was its attention to linear growth and parallel lines, which he attributed to our flawed notion of a flat earth that extended to infinity, and a single direction for “up,” the equal and opposite direction of our “down-to-earth” sensibilities. Nature, if unconstrained, prefers radial (outward-inward) growth with circumferential (precessional-perpendicular) constraints.

The 12-strut tensegrity sphere approximates the overall shape of the VE, and perfectly models what Fuller meant by this. Like all his tensegrities, its structural integrity is maintained by a balance between the radial compression of its struts, and the circumferential tension of its tendons. The twelve-strut tensegrity sphere will torque naturally into the tensegrity octahedron, a transformation recapitulated in the vector model of the jitterbug.

The VE consists of four great circles, i.e., four 3-strut triangles in the twelve-strut tensegrity sphere, or four hexagons in the vector model.

It is likely no coincidence that the surface area of the sphere is equal to the combined surface areas of the VE’s four great-circle disks. The two sides of each disk account for both the convex external surface of the sphere and its concave internal surface. (See: Anatomy of a Sphere.) In the bow-tie construction of the VE, produced by folding the great circle disks along the VE’s central 60° angles, both surfaces are exposed, one inside the square faces, the convex, energy-dispersing surface, and the other inside the triangular faces, the concave, energy-focusing surface. This interpretation of the bow-tie model is strengthened by the quanta model in which the square faces expose the energy-dissipating B modules, and the triangular faces expose the energy-conserving A modules. (See: A and B Quanta Modules.)

The Seven Axes of Symmetry common to all the regular polyhedra correspond to the 4 axes of spin running through the VE’s eight triangular faces, plus the 3 axes running through its six square faces, the former disclosing spherical VE and its four great circles, and the latter disclosing the spherical octahedron and its three great circles.

Transformations of the VE disclose the regular icosahedron, the Jessen icosahedron (or six-strut tensegrity sphere), the regular octahedron, and the regular tetrahedron. The transformation to the regular icosahedron is perhaps best modeled in the radial close packing of spheres. With the removal of the central sphere, the twelve remaining spheres naturally reposition themselves into the shape of the icosahedron.

The transformation to the Jessen orthogonal icosahedron is perhaps best modeled in the jitterbugging of the six-strut tensegrity, or tensegrity tetrahedron which, in its most relaxed, spherical, or equilibrium state is identical with the Jessen icosahedron.

The transformation to the regular octahedron is disclosed through torquing of the 12-strut tensegrity (see above), but is perhaps most convincingly modeled in the jitterbug transformation by the coordinated rotations of its eight triangular faces.

The transformation of the VE into the regular tetrahedron can be accomplished in the vector model by adding a 180° twist to the downward motion of the jitterbug.

But the transformation of the VE into a tetrahedron is perhaps best modeled in the six-strut tensegrity sphere (aka Jessen icosahedron) which occurs at the precise midpoint of the jitterbug transformation. (See: Icosahedron Phases of the Jitterbug.) From here, the VE may continue its transformation into the octahedron, or it can be torqued into the shape of a regular tetrahedron. A clockwise or counter-clockwise torque will produce either a positive or a negative tetrahedron. (See: The Dual Nature of the Tetrahedron.)

For me, the most compelling model of the jitterbug transformation, which Fuller identified with wave-particle duality, the equivalence of mass and energy, the balance of disintegrative, radiational forces (compression) with integrative, gravitational forces (tension), and which he intuited as a generative metaphor for nearly everything in the physical sciences, if not for everything that is thinkable, is the following: eight, six-strut tensegrity spheres surrounding a common center, and transforming between positive and negative tetrahedra.

This model is illustrated below, with four of the eight, six-strut tensegrity spheres torquing clockwise to form the positive tetrahedron, and the other four torquing counter-clockwise to form the negative tetrahedron, which then switch roles to reverse the process. The result is an oscillation between the VE, with the eight tetrahedra all sharing a common vertex at its center, and the octahedron, with the eight tetrahedra projecting from its eight faces. In the context of the isotropic vector matrix, all the vertices of all the tetrahedra always converge on the center of a VE, but these convergences shift by one-half wavelength with each cycle, exchanging the nuclear spheres (vertex convergences) at the centers of the VEs, with the nuclear space at the centers of the octahedra. (See also: Spheres and Spaces.)

“The tetrakaidecahedron develops from a progression of closest-sphere-packing symmetric morphations at the exact maximum limit of one nuclear sphere center’s unique influence, just before another nuclear center develops an equal magnitude inventory of originally unique local behaviors to that of the earliest nuclear agglomeration.“
— R. Buckminster Fuller, Synergetics, section 942.71

Note: For instructions on how to construct the Weaire-Phelan structure, see my post, Construction Method for the Pyritohedron and Tetrakaidecahedron of the Weaire-Phelan Structure.

The tetrakaidecahedron that Buckminster Fuller had in mind, and which he refers to as “Lord Kelvin’s Solid” was the truncated octahedron, a polyhedron which, like the vector equilibrium (VE), has fourteen sides, and which at the time (1975) was considered the tentative solution to the Kelvin Problem: How can space be partitioned into cells of equal volume with the least area of surface between them? Fuller, like most others, assumed that a bitruncated cubic honeycomb consisting of truncated octahedron cells was, with only slight deformation, the most likely solution. Ten years after Fuller’s death, in 1993, Denis Weaire of Trinity College Dublin and his student Robert Phelan showed through computer simulations of foam that a combination of pyritohedra and tetrakaidecahedra of equal volume could fill space more efficiently, with a surface area to volume ratio 0.3% less that that of Kelvin’s truncated octahedra.

There is a curious correlation between the close packing of unit-radius spheres and foams of unit-volume cells. Spheres close pack around a central sphere as vector equilibria of increasing frequency. The polyhedral domain of each sphere is a rhombic dodecahedron. Rhombic dodecahedra close pack exactly as spheres close pack, twelve around one. (See The Rhombic Dodecahedron.) If we partition close-packed spheres into nuclear domains of central spheres surrounded by unique 12-sphere shells, the shells are distributed as Kelvin’s tetrakaidecahedra, but the nuclei themselves are distributed exactly as the pyritohedra are distributed in the Weaire-Phelan matrix. See: Formation of New Nuclei in Close-Packing of Spheres.

Both the bitruncated cubic honeycomb consisting of truncated octahedra, and the Weaire-Phelan matrix consisting of pyritohedra and tetrakaidecahedra, isolate unique nuclei in the close-packed spheres of the isotropic vector matrix. In the figure below, the isolated nuclei are shown as red spheres, and those that share their shells with neighboring nuclei are shown as pink spheres. In the top row, the vector equilibria of the isotropic vector matrix surround both the red and pink nuclei; they do not distinguish unique nuclei. The truncated octahedra in the middle row do distinguish unique nuclei if their edge length is equal to the sphere diameter, with every other nuclear domain sharing a common center with a truncated octahedron. The Weaire-Phelan matrix (bottom row) distinguishes unique nuclei by their own polyhedron, the pyritohedron, while those that share their shells with neighboring nuclei are centered between positive and negative tetrakaidecahedra. The tetrakaidecahedra are sized so that their circumsphere radius is equal the the sphere diameter.

The pyritohedron is familiar as its namesake, the pyrite crystal, or “fool’s gold,” which like the regular dodecahedron has twelve identical faces. The pentagonal faces of the pyritohedron are irregular, with one edge slightly longer that the other four. The pyritohedron can be derived from the Jessen Orthogonal Icosahedron, more familiar in Fuller’s geometry as the convex shape of the six-strut tensegrity sphere. The correlation is intriguing. See also: Tensegrity, and Icosahedron Phases of the Jitterbug.

The pyritohedron can be constructed by the addition of eight shallow tetrahedra to each of the eight equilateral triangles of the Jessen icosahedron. The height of these tetrahedra is exactly 1/3 the in-sphere radius of the Jessen icosahedron, or one quarter the circumsphere radius of the pyritohedron.

An even more beautiful symmetry, I think, is disclosed by connecting the peaks of the eight shallow tetrahedra to form a cube.

The tetrakaidecahedron that combines with the pyritohedron to fill all space is a 14-sided polyhedron consisting of two elongated hexagonal faces and two sets of pentagonal faces: four matching the faces of the pyritohedron, and eight elongated pentagons.

Lines drawn from the base to peak of the eight elongated pentagon faces, and from the line’s endpoints to the center of the tetrakaidecahedron, form equilateral triangles whose edge lengths in the Weaire-Phelan matrix correspond to the diameter of the nuclear spheres isolated by the pyritohedra.

The appearance of eight equilateral triangles in both the pyritohedron and the tetrakaidecahedron suggests the possibility of a jitterbug-like transformation from one to the other. Their edge lengths, however, differ. The edge length of the eight equilateral triangles in the pyritohedron is approximately 1.091135 times the edge length of those in the tetrakaidecahedron.

Connecting the unit-length radials of adjacent tetrakaidecahedra forms shells around the nuclei in the shape of Kelvin’s truncated octahedron.

If we align the unit vectors of the Weaire-Phelan matrix with the isotropic vector matrix, the pyritohedra enclose spaces rather than spheres. If we align them with the distribution of nuclei, the Weaire-Phelan matrix is 180° out of phase with the isotropic vector matrix. This phase difference suggests an energetic relationship between the two matrices that may provide insight into the jitterbug transformation, and its oscillations between spheres and spaces.

The pyritohedron, and the tetrakaidecahedra paired with its mirror image, both align with the The Seven Axes of Symmetry.

All polyhedra are either left- or right-handed and, with the exception of the tetrahedron, there is no transformation that can be modeled by which one becomes the other. The handedness of a polyhedron is not readily apparent when viewed as a solid or as a vector model with single-point vertices. However, when modeled structurally as tensegrities their handedness becomes obvious.

The tetrahedron is uniquely ambidextrous. From its relaxed state as the six-strut tensegrity sphere, it is both itself and its inverse. The transformation can go either way, producing either a positive or a negative tetrahedron. All configurations between the spherical and polyhedron phases are structurally stable, but once the choice is made to transform either in a clockwise or counterclockwise direction the ambiguity collapses into into either a positive or a negative tetrahedron. To transform back to its inverse, the tetrahedron must first pass through its spherical phase. For more information, see Tensegrity.

The Jitterbug is an oscillation between positive and negative (left-handed and right-handed, clockwise and counter-clockwise) tetrahedra.

The bow-tie construction of the rhombic dodecahedron has an extra arc along the short diagonal of each of its rhomboid faces. Removing the extra arc discloses the spherical rhombic dodecahedron as the equivalent of two tetrahedra, one positive and one negative.

For more information, see Great Circle Bow-Ties of the VE.

Turning a regular tetrahedra inside-out, i.e., forcing a vertex through its opposite face (the tetrahedron is the only regular polyhedron that can do this), produces either the star tetrahedron, or the tetrahelix, and neither close-pack to fill all-space. In fact, it’s possible that no two tetrahedra in the helical and star structures produced by serial inside-outing will ever have precisely the same orientation in a fixed coordinate system. Fuller may have attributed the difference between the tetrahedron’s mirror-image, inside-outing polarity and its rotational, axial polarity to the multiplicative (concave-convex) vs. additive (polar) duality of all polyhedral systems. (See: The Multiplicative and Additive Two.)

Perhaps a more interesting model of the tetrahedron turning itself inside out is one that results in an octahedron rather than another tetrahedron. The faces of the regular octahedron can be unfolded like the petals of flower to produce two tetrahedra, one positive and one negative with rotational (non-mirror-image) polarity. The rotation along the fold lines is exactly 180° from tetrahedron to octahedron, or from octahedron to tetrahedron. We may conclude that the octahedron is two tetrahedra turned inside out.

That the octahedron’s volume is 4 compared with the tetrahedra’s combined volume of 2 suggests a transformative model for the tetrahedron’s fundamental and inseparable duality.

Note: Fuller often remarked on the tetrahedron’s unique ability to turn itself inside out, i.e., any one of its vertices may be passed through its opposite face, thereby exchanging inside for outside like a rubber glove. For me, however, this process isn’t so much an oscillation between positive and negative tetrahedra, which is a four-dimensional phenomenon of the jitterbug transformation, but rather, a linear (or helical) phenomenon in two dimensions. See: Tetrahelix.

The regular icosahedron can be nested inside the regular octahedron so that eight of its faces are coincident with the eight faces of the enclosing octahedron.

The icosahedron’s face is skewed at an angle of 37.76125° (arctan(√(3/5)) from the face of the octahedron and divides its edges into lengths corresponding to golden ratio (Φ).

The same relationship is disclosed in the 31 great circles of the icosahedron. The faces of both the spherical octahedron and the spherical icosahedron are divisible by whole numbers of the Basic Disequilibrium LCD Triangle.

The projection of the Basic Disequilibrium LCD Triangle onto the regular icosahedron discloses the same angles at which the icosahedron’s face is skewed from the face of its enclosing octahedron: 37.76125° (arctan(√(3/5)) and 82.23875° (arctan(√(5/3)+30°).

The angles at which the icosahedron’s face is skewed from the face of the enclosing octahedron are identical with the angles of rotation in the jitterbug corresponding to the space-filling complement to the regular icosahedron. See: Icosahedron Phases of the Jitterbug.

Note further that all of the surface angles in the icosahedron projection of the spherical LCD triangle are identical with the rotations in the jitterbug: the regular icosahedron at 22.23875° (arctan(√(5/3)-30°) and 97.76125° (arctan(√(3/5)+60°); the Jessen icosahedron or tensegrity equilibrium at 30° and 90°; the space-filling complement to the regular icosahedron at 37.76125° (arctan(√(3/5)) and 82.23875° (arctan(√(5/3)+30°), and the regular octahedron at 60°.